信州大学(理系) 2025年　問題6


$0 \leqq x \leqq 2\pi \ \ において、2\ 曲線 \ \ y=|\sin x | ,\ \ y=-\cos 2x \ \ によって囲まれた図形の面積を求めよ。$
$また、この図形を \ x\ 軸のまわりに \ 1\ 回転させてできる回転体の体積を求めよ。$

　

$点P(x,\ y)\ の直線 \ \ x=\pi \ \ における対称な点をP'(x',\ y')\ \ とすると$

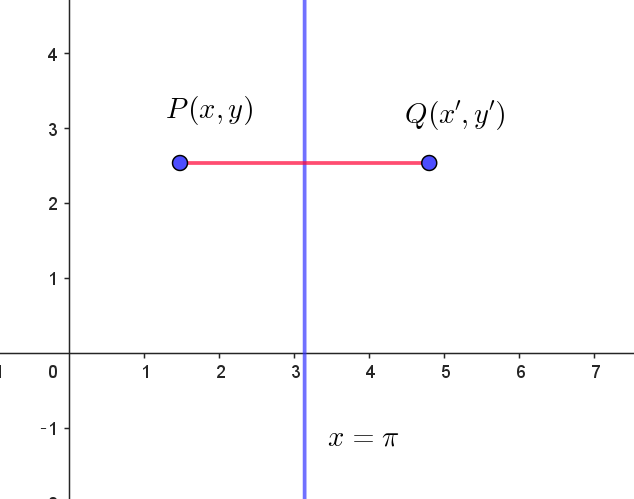
$\dfrac{x+x'}{2}=\pi,\quad y=y' $

$点P(x,\ y)\ が \ \ y=|\sin x|\ \ 上にあると$

$y'=|\sin(2\pi -x')|=|\sin(-x')|=|\sin x'|$

$よって \quad 点P'(x',\ y') \ \ は \ \ y=|\sin x| \ \ 上にある。$

$点P(x,\ y)\ \ が \ \ y=-\cos 2x \ \ 上にあると$

$y'=-\cos 2(2\pi - x')=-\cos (-2x')=-\cos 2x'$

$よって \quad 点P'(x',\ y')\ \ は \ \ y=-\cos 2x \ \ 上にある。$

$したがって、y=|\sin x|\ \ と \ \ y=-\cos 2x \ \ は直線 \ \ x=\pi \ \ で対称である。$

$(1)\ \ 面積$

　

$2\ 曲線 \ \ y=|\sin x | ,\ \ y=-\cos 2x \ \ によって囲まれた図形の$

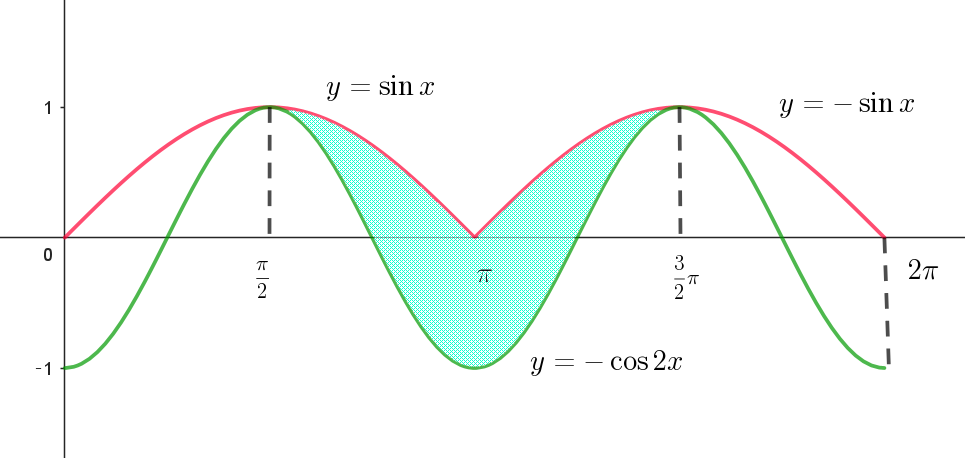
$面積を \ 2S\ \ とすると$

\begin{eqnarray*} S &=&\int_{\frac{\pi}{2}}^{\pi} (\sin x +\cos 2x)dx\\ \\ &=&\big[-\cos x + \dfrac{1}{2}\sin 2x \big]_{\frac{\pi}{2}}^{\pi}\\ \\ &=&1 \end{eqnarray*}
$よって求める面積は \quad 2S=2$


$(2)\ \ 体積$

$\dfrac{3}{4}\pi \leqq x \leqq \pi \ \ で \ \ y=\sin x \ \ と \ \ y=\cos 2x \ \ の交点の \ x\ 座標は$

$\sin x=\cos 2x$

$\sin x=1-2\sin ^2x$

$2\sin ^2x+\sin x -1=0$

$(\sin x +1)(2\sin x-1)=0$

$\sin x=\dfrac{1}{2}$

$x=\dfrac{5}{6}\pi$

　

$したがって$

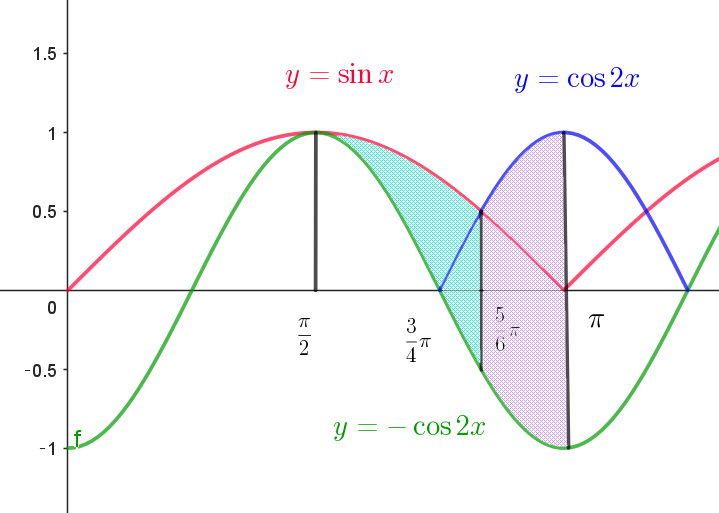
$\dfrac{\pi}{2} \leqq x \leqq \dfrac{5}{6}\pi \ \ のとき \quad \sin x \geqq |\cos 2x|$

$\dfrac{5}{6}\pi \leqq x \leqq \pi \ \ のとき \quad \sin x \leqq \cos 2x$

$2\ 曲線 \ \ y=|\sin x | ,\ \ y=-\cos 2x \ \ によって囲まれた図形を$

$x\ 軸のまわりに \ 1\ 回転させてできる回転体の体積を \ 2V\ とすると$

\begin{eqnarray*} V &=&\pi \int_{\frac{\pi}{2}}^{\frac{5}{6}\pi} \sin ^2xdx -\pi \int_{\frac{\pi}{2}}^{\frac{3}{4}\pi} (-\cos 2x)^2dx+ \pi \int_{\frac{5}{6}\pi}^{\pi} \cos ^2 2x dx\\ \\ &=&\pi \int_{\frac{\pi}{2}}^{\frac{5}{6}\pi} \dfrac{1-\cos 2x}{2}dx -\pi \int_{\frac{\pi}{2}}^{\frac{3}{4}\pi} \dfrac{1+\cos 4x}{2}dx+ \pi \int_{\frac{5}{6}\pi}^{\pi} \dfrac{1+\cos 4x}{2}dx\\ \\ &=&\dfrac{\pi}{2}\big\{\big[x-\dfrac{1}{2}\sin 2x\big]_{\frac{\pi}{2}}^{\frac{5}{6}\pi} - \big[x+\dfrac{1}{4}\sin 4x \big] _{\frac{\pi}{2}}^{\frac{3}{4}\pi} + \big[x+\dfrac{1}{4}\sin 4x \big]_{\frac{5}{6}\pi}^{\pi} \big\}\\ \\ &=&\dfrac{\pi}{2}\big\{\big(\dfrac{5}{6}\pi -\dfrac{1}{2}\sin \dfrac{5}{3}\pi -\dfrac{\pi}{2} + \dfrac{1}{2}\sin \pi\big)- \big(\dfrac{3}{4}\pi + \dfrac{1}{4}\sin 3\pi -\dfrac{\pi}{2} - \dfrac{1}{4}\sin 2\pi\big)+ \big(\pi + \dfrac{1}{4}\sin 4\pi -\dfrac{5}{6}\pi - \dfrac{1}{4}\sin \dfrac{10}{3}\pi\big)\big\}\\ \\ &=&\dfrac{\pi}{2}\big\{\big(\dfrac{5}{6}\pi -\dfrac{1}{2} \times (-\dfrac{\sqrt{3}}{2}) -\dfrac{\pi}{2} - \dfrac{3}{4}\pi +\dfrac{\pi}{2} +\pi -\dfrac{5}{6}\pi - \dfrac{1}{4} \times (-\dfrac{\sqrt{3}}{2})\big\}\\ \\ &=&\dfrac{\pi}{2}\big(\dfrac{\pi}{4} + \dfrac{3\sqrt{3}}{8}\big)\\ \end{eqnarray*}
$よって求める体積は \quad 2V=\pi \big(\dfrac{\pi}{4} + \dfrac{3\sqrt{3}}{8}\big)$

ページの先頭へ↑




メインメニュー　に戻る