信州大学(理系) 2025年 問題4
$a\ は実数とする。関数 \ f(x)\ を \ \ f(x)=x^3-3(a+2)x^2+24ax-2a^2-41a+28 \ \ と定めるとき、以下の問い$
$に答えよ。$
$(1)\ \ f(2) \geqq 0 \ \ となるとき、a\ のとり得る値の範囲を求めよ。$
$(2)\ \ x \geqq 2 \ \ となるすべての \ x\ に対して \ \ f(x) \geqq 0 \ \ が成り立つとき、a\ のとり得る値の範囲を求めよ。$
(1)
$f(2)=2^3-3(a+2) \times 2^2+24a \times 2-2a^2-41a+28=-2a^2-5a+12$
$f(2) \geqq 0 \quad より \quad 2a^2+5a-12 \leqq 0$
$(a+4)(2a-3) \leqq 0$
$-4 \leqq a \leqq \dfrac{3}{2}$
(2)
$f'(x)=3x^2-6(a+2)x+24a=3\big(x^2-2(a+2)x+8a\big)=3(x-2a)(x-4)$
$f'(x)=0 \quad より \quad x=2a,\ \ 4$
$一般に、3\ 次の係数が正の \ 3\ 次関数のグラフは、f'(x)=0\ \ の解が異なる \ 2\ つの実数解 \ \ \alpha,\ \ \beta \ \ (\alpha < \beta)\ \ を$
$もつならば \quad x=\alpha \ \ で極大となり、x=\beta \ \ で極小となる。$
(i)$\ \ 2a \leqq 2 \quad のとき、すなわち \quad a \leqq 1 \quad のとき$
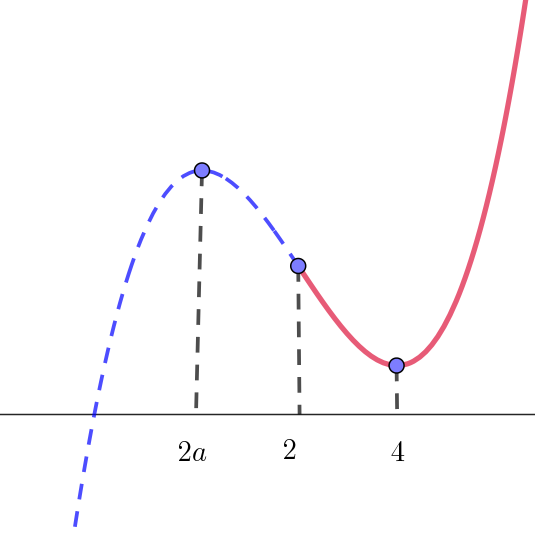
$\quad 条件は \quad f(4) \geqq 0$
$\quad f(4)=4^3-3(a+2) \times 4^2+24a \times 4-2a^2-41a+28=-2a^2+7a-4$
$\quad 2a^2-7a+4 \leqq 0$
$\quad \dfrac{7-\sqrt{17}}{4} \leqq a \leqq \dfrac{7+\sqrt{17}}{4}$
$\quad \dfrac{7-\sqrt{17}}{4} < 1 < \dfrac{7+\sqrt{17}}{4} \quad だから$
$\quad \dfrac{7-\sqrt{17}}{4} \leqq a \leqq 1 $
(ii)$\ \ 2 < 2a < 4 \quad のとき、すなわち \quad 1 < a < 2 \quad のとき$
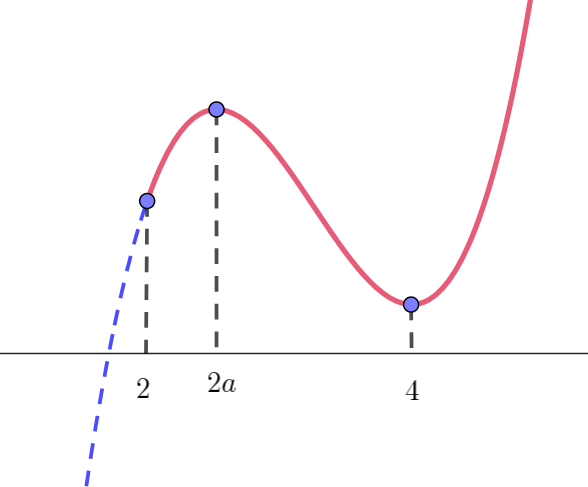
$\quad 条件は \quad f(2) \geqq 0 \quad かつ \quad f(4) \geqq 0$
$\quad f(2) \geqq 0 \quad より \quad -4 \leqq a \leqq \dfrac{3}{2}$
$\quad f(4) \geqq 0 \quad より \quad \dfrac{7-\sqrt{17}}{4} \leqq a \leqq \dfrac{7+\sqrt{17}}{4} $
$\quad -4 < \dfrac{7-\sqrt{17}}{4} < 1 < 2 < \dfrac{7+\sqrt{17}}{4} \quad だから$
$\quad 1 < a \leqq \dfrac{3}{2}$
(iii)$\ \ 4 < 2a \quad のとき、すなわち \quad 2 < a \quad のとき$
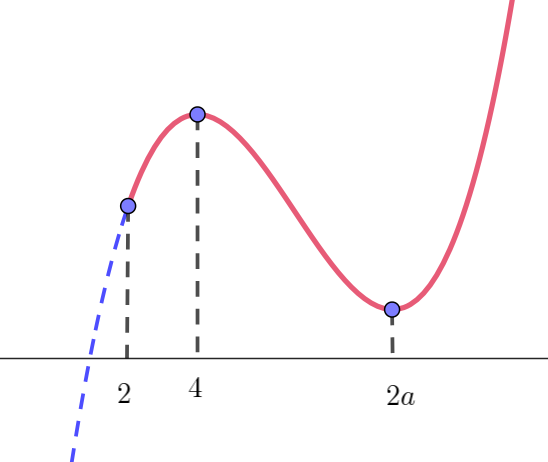
$\quad 条件は \quad f(2) \geqq 0 \quad かつ \quad f(2a) \geqq 0$
$\quad f(2) \geqq 0 \quad より \quad -4 \leqq a \leqq \dfrac{3}{2} \quad だから$
$\quad したがって これを満たす \ a\ はない。$
(iv)$\ \ 2a=4 \quad のとき、すなわち \quad a=2 \quad のとき$
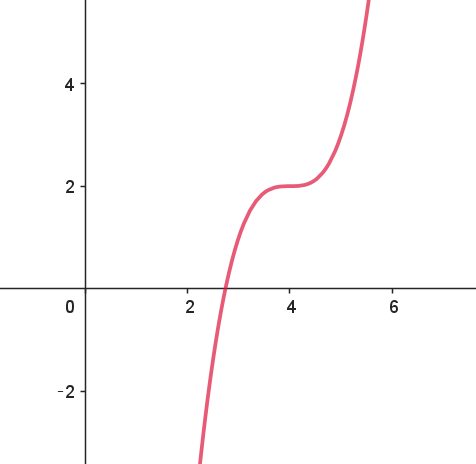
$\quad f'(x)=3x^2-24x+48=3(x-4)^2 \geqq 0 \quad だから$
$\quad f(x)\ \ は単調増加$
$\quad 条件は \quad f(2) \geqq 0 $
$\quad f(2)=2^3-12 \times 2^2+48 \times 2-62=-6$
$\quad よって 条件を満たさない$
(i) ~(iv)$\ \ より \quad \dfrac{7-\sqrt{17}}{4} \leqq a \leqq \dfrac{3}{2} $
メインメニュー に戻る