信州大学(理系) 2025年　問題3


$平面上に三角形ABC\ と動点P\ がある。ある実数 \ k\ について、PA^2+2PB^2+3PC^2=k\ \ を満たすように$
$点P\ が動くとき、点P\ は円を描く。この円の中心を \ O\ とするとき、以下の問いに答えよ。$
$(1)\ \ \vec{OC} \ を \ \vec{OA} ,\ \ \vec{OB}\ \ を用いて表せ。$
$(2)\ \ 三角形OAB,\ \ OBC,\ \ OCA \ \ の面積をそれぞれ \ S_1,\ S_2,\ S_3 \ とする。このとき、S_1:S_2:S_3 \ \ を求めよ。$


(1)


$円の中心O\ を始点とするベクトルで表し、\vec{OA}=\vec{a},\ \ \vec{OB}=\vec{b},\ \ \vec{OC}=\vec{c},\ \ \vec{OP}=\vec{p}\ \ とおく。$

$条件 \quad PA^2+2PB^2+3PC^2=k\ \ をベクトルで表現すると$

$|\vec{a}-\vec{p}|^2+2|\vec{b}-\vec{p}|^2+3|\vec{c}-\vec{p}|^2=k$

$\{|\vec{a}|^2-2\vec{a}\cdot \vec{p} +|\vec{p}|^2\}+2\{|\vec{b}|^2-2\vec{b}\cdot \vec{p} +|\vec{p}|^2\}+3\{|\vec{c}|^2-2\vec{c}\cdot \vec{p} +|\vec{p}|^2\}=k$

$6|\vec{p}|^2 -2(\vec{a}+2\vec{b} +3\vec{c})\cdot \vec{p} +|\vec{a}|^2+ 2|\vec{b}|^2+ 3|\vec{c}|^2=k$

$|\vec{p}|^2 -\dfrac{\vec{a}+2\vec{b} +3\vec{c}}{3} \cdot \vec{p} =\dfrac{1}{6}\big(k-|\vec{a}|^2- 2|\vec{b}|^2- 3|\vec{c}|^2\big)$

$\Big|\vec{p} -\dfrac{\vec{a}+2\vec{b} +3\vec{c}}{6}\big|^2=\dfrac{1}{6}\big(k-|\vec{a}|^2- 2|\vec{b}|^2- 3|\vec{c}|^2+\dfrac{1}{6}|\vec{a}+2\vec{b} +3\vec{c}|^2 \big)$

　

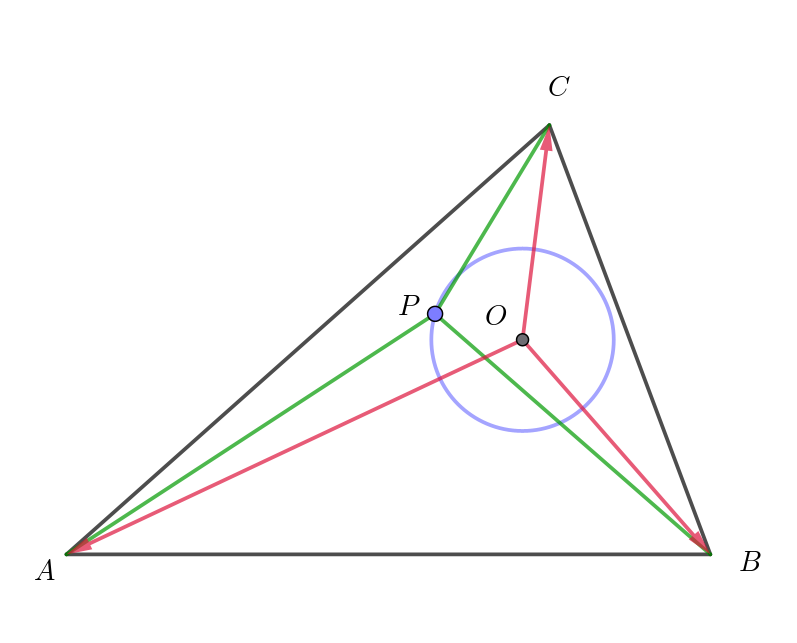
$これより、点P\ は中心(\dfrac{\vec{a}+2\vec{b} +3\vec{c}}{6})\ \ の円を描くから$

$\vec{a}+2\vec{b} +3\vec{c} =\vec{0}$

$\vec{c}=-\dfrac{\vec{a}+2\vec{b}}{3}$

$すなわち \quad \vec{OC}=- \dfrac{\vec{OA}+2\vec{OB}}{3}$

(2)

　

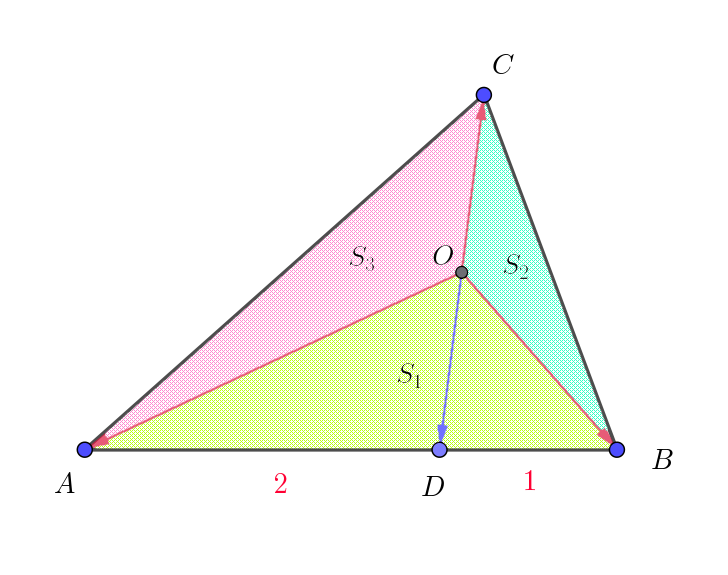
$\vec{OD}= \dfrac{\vec{OA}+2\vec{OB}}{3} \quad とおくと$

$点D\ は辺AB\ を \ 2:1 \ に内分する点であり、$

$\vec{OD} \ は \ \vec{OC} \ の逆ベクトルだから \quad OD=OC$

$よって$

$\triangle OBD=\triangle OBC=S_2$

$\triangle ODA=\triangle OCA=S_3$

$また、\triangle OBD:\triangle ODA=DB:AD=1:2$

$S_2:S_3=1:2 \ \ より \quad S_3=2S_2$

$また、\triangle OAB=\triangle OBD+\triangle ODA=S_2+S_3　\quad だから$

$S_1=S_2+S_3=S_2+2S_2=3S_2$

$\therefore \ \ S_1:S_2:S_3=3S_2:S_2:2S_2=3:1:2$


ページの先頭へ↑




メインメニュー　に戻る