埼玉大学(理系) 2021年 問題2
$a,\ b,\ c,\ d\ を実数とし、f(x)=x^4+ax^3+bx^2+cx+d \ \ とおく。f(0),\ f(1),\ f(2)\ は整数であり、$
$f(-1)=f(1)\ \ とする。次の問いに答えよ。$
$(1)\ \ c=-a \ \ を示せ。$
$(2)\ \ 3f(0)-4f(1)+f(2)\ \ が \ 6\ の倍数であることは、a,\ b,\ c,\ d\ がすべて整数であることの必要十分条件$
$\qquad であることを示せ。$
$(3)\ \ f(0) \geqq 0,\ f(1)=0,\ \ f(2) \geqq 0 ,\ \ 3f(0)+f(2) \leqq 100 \ \ をすべて満たす整数の組 \ (a,\ b,\ c,\ d)\ は何通り$
$\qquad あるか求めよ。$
$(解説)$
$(1)\ \ 誰しもが点数をもらえる問題です。$
$(2)\ \ f(0),\ f(1),\ f(2)\ が整数から、a,\ b,\ c,\ d\ が整数になることを導きます。$
$(3)\ \ 順序対 \ (a,\ b)\ を座標ととらえて、格子点の個数を調べます。$
(1)
$\quad f(x)=x^4+ax^3+bx^2+cx+d \quad で \quad f(-1)=f(1) \quad だから$
$\quad 1-a+b-c+d=1+a+b+c+d \qquad \therefore \ \ c=-a$
(2)
$\quad f(0)=d \quad で \ f(0)\ は整数だから \quad d\ は整数$
$\quad f(1)=1+a+b+c+d=b+d+1 \quad より \quad b=f(1)-f(0)-1 \qquad f(0),\ f(1)\ \ は整数だから \ b\ は整数$
$\quad f(2)=16+8a+4b+2c+d=6a+4b+d+16 \quad より $
\begin{eqnarray*} 6a &=&f(2)-4b-d-16\\ \\ &=&f(2)-4\{f(1)-f(0)-1\}-f(0)-16\\ \\ &=&3f(0)-4f(1)+f(2)-12\\ \end{eqnarray*}
$\quad 3f(0)-4f(1)+f(2) \quad が \ 6\ の倍数ならば、3f(0)-4f(1)+f(2)=6k \ \ (kは整数)\ とおくと$
$\qquad 6a=6k-12 \qquad \ \ \therefore \ \ a=k-2 \ \ となり \ \ a\ は整数、c=-a \ \ より \ \ c\ も整数$
$\qquad したがって \quad a,\ b,\ c,\ d\ は整数$
$\quad 逆に \quad a,\ b,\ c,\ d\ は整数ならば$
$\qquad 3f(0)-4f(1)+f(2)=6a+12=6(a+2) \quad は \ 6\ の倍数$
(3)
$a\ が整数ならば \ c\ も整数であり、d\ は整数であるから$
$整数の組 \ (a,\ b,\ c,\ d)\ の個数と整数の組 \ (a,\ b)\ の個数は一致する。$
(i)$\ \ f(0) \geqq 0 \quad より \quad d \geqq 0$
(ii)$\ \ f(1)=b+d+1=0 \quad より \quad d=-b-1 \geqq 0 \quad したがって \quad b \leqq -1$
(iii)$\ \ f(2) \geqq 0 \quad より \quad 6a+4b+d+16 \geqq 0 $
$\qquad 6a+4b+(-b-1)+16 \geqq 0 \qquad \therefore \ \ 2a+b+5 \geqq 0$
(iv)$\ \ 3f(0)+f(2) \leqq 100 \quad より \quad 3d+(6a+4b+d+16) \leqq 100 $
$\qquad 6a+4b+4d \leqq 84 \qquad 3a+2b+2d \leqq 42 $
$\qquad 3a+2b+2(-b-1) \leqq 42 \qquad 3a \leqq 44 \qquad \therefore \ \ a \leqq \cfrac{44}{3}$
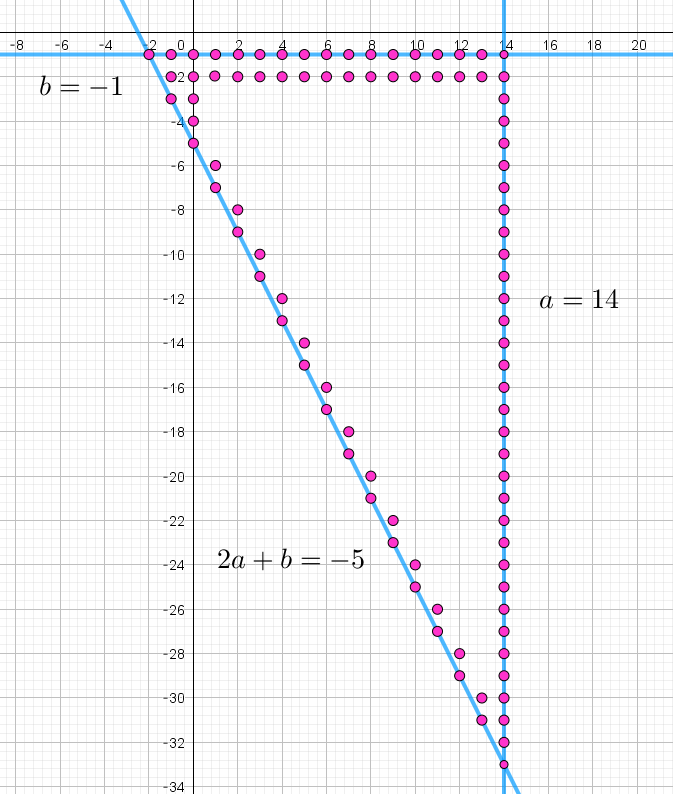
(i)~(iv)$\ より \quad a \leqq 14,\quad b \leqq -1 \quad 2a+ b \geqq -5$
$を満たす整数の組 \ (a,\ b)\ を求めればよい。$
$(a,\ b)\ を座標平面上の点と考えれば、この不等式をみたす領域は$
$右図のような三角形の内部で、その格子点の個数を求めることになる。$
$a\ を1\ つ定めると、b\ は \ \ -2a-5 \ \ から \ \ -1\ \ までの$
$-1-(-2a-5)+1=2a+5 \ \ 個あるから求める個数 \ N\ は$
\begin{eqnarray*}
N
&=&\sum _{a=-2}^{14} (2a+5) \qquad k=a+3 \quad とおくと\\
\\
&=&\sum _{k=1}^{17} (2(k-3)+5)\\
\\
&=&\sum _{k=1}^{17} (2k-1)\\
\\
&=&2 \times \cfrac{17 \times 18}{2}-17\\
\\
&=&289
\end{eqnarray*}
\begin{eqnarray*}
\end{eqnarray*}
メインメニュー に戻る