無限に深い井戸型ポテンシャル
$シュレディンガー方程式の例題1はどの本でもこのポテン$
$シャルです。理由は簡単で、すぐ解けるからです。$
$それでは解いてみましょう。$
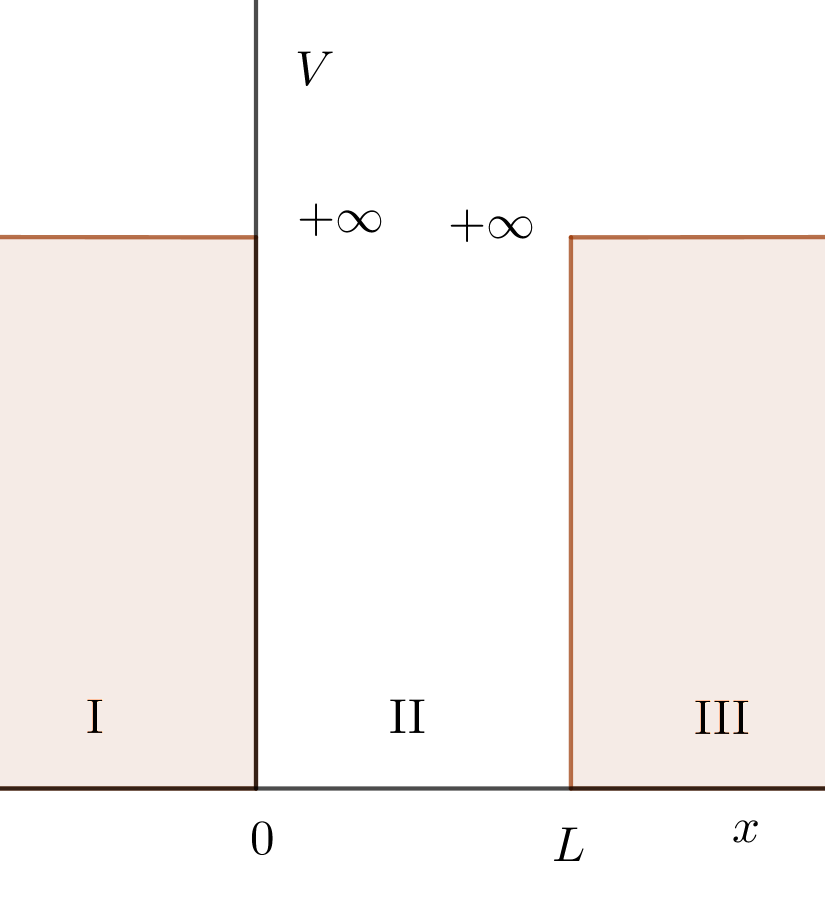
$右図のようなポテンシャル$
\[V(x)=
\left\{ \begin{array}{l}
\infty \hspace{2em} (x < 0)\\
0 \hspace{3em} (0 \leqq x \leqq L )\\
\infty \hspace{2em} (x >L)\\
\end{array} \right.
\]
$内を1次元運動する量子は、領域Ⅰ,Ⅲでは、無限の$
$運動エネルギーが必要になるので存在できません。$
$領域Ⅱでのシュレディンガー方程式は$
$\qquad -\cfrac{\hbar ^2}{2m} \cfrac{d^2 }{dx^2}\varphi(x) =E\varphi(x) \hspace{19em}(1)$
$\quad k^2=\cfrac{2m}{\hbar ^2}E \ \ とおくと \quad (1)は \qquad \cfrac{d^2 }{dx^2}\varphi(x) =-k^2\varphi(x) \hspace{7em}(2)$
$(1)\ \ シュレディンガー方程式(2)の解$
$これは単振動の微分方程式だから解は \quad \varphi(x)=A\cos kx+B\sin kx $
$境界条件より$
$\quad \varphi(0)=0 \ \ だから A=0$
$\quad \varphi(L)=0 \ \ だから B\sin kL=0 \qquad \therefore k=\cfrac{n \pi}{L} \quad (n=1,2,3,\cdots )$
$あらためて \varphi(x) を \varphi _n(x) \ \ とおくと$
\begin{eqnarray*}
\varphi _n(x)&=&B\sin kx\\
&=&B\sin \cfrac{n\pi}{L}x \quad (n=1,2,3,\cdots )\\
\end{eqnarray*}
$積分定数Bは規格化条件より定まります。$
\[\int _{-\infty}^{\infty}|\varphi _n |^2 dx=1 \ \ より\]
\[B^2\int _0^L\sin ^2 \cfrac{n\pi}{L}x dx=1\]
\[B^2\int _0^L \cfrac{1}{2}(1-\cos \cfrac{2n\pi}{L}x) dx=1\]
\[\cfrac{B^2}{2}\Bigl[x-\cfrac{L}{2n\pi}\sin \cfrac{2n\pi}{L}x \Bigr]_0^L=1\]
\[\cfrac{B^2}{2}L=1\]
$B=\sqrt{\cfrac{2}{L}}$
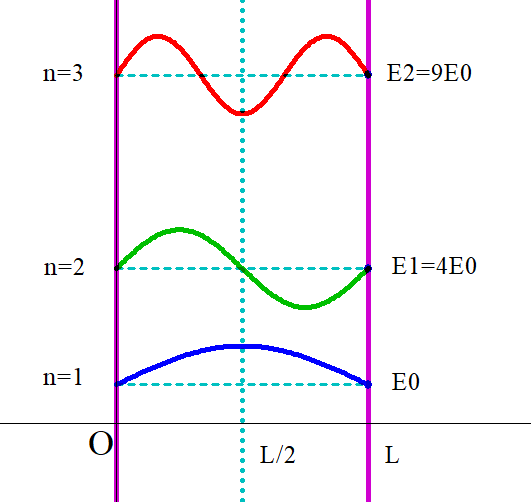
$\therefore \varphi _n(x)=\sqrt{\cfrac{2}{L}}\sin \cfrac{n\pi}{L}x \quad (n=1,2,3,\cdots )$
$nは量子状態を決定するので量子数といいます。$
$(2)\ \ エネルギー固有値$
$(1) より \quad E=\cfrac{\hbar ^2}{2m}k^2=\cfrac{\hbar ^2 \pi ^2}{2mL^2}n^2$
$これより、エネルギー固有値は離散的であることがわかります。$
$n=1 \ \ のとき E_0=\cfrac{\hbar ^2 \pi ^2}{2mL^2} \ \ を基底状態といいます。$
$n=2,3 \cdots \ とするとエネルギー固有値は2乗に比例して増加しますが、これを励起状態$
$といいます。$
$(3)\ \ 位置の期待値$
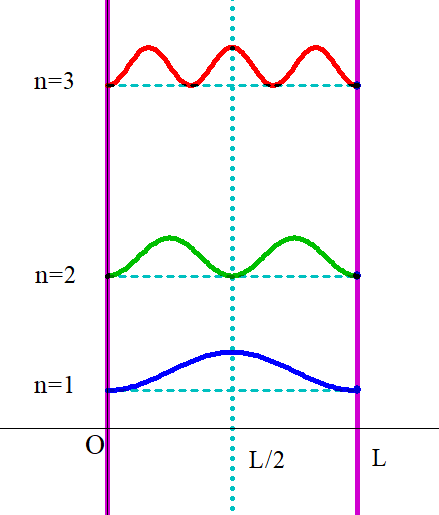
$量子の確率密度関数|\varphi _n(x)|^2 は、右図のとおりで$
$n=1 のときは、x=\cfrac{L}{2} \ \ のあたり$
$n=2 のときは、x=\cfrac{L}{4}, \ \cfrac{3L}{4} \ \ のあたり$
$n=3 のときは、x=\cfrac{L}{6}, \ \cfrac{L}{2},\ \cfrac{5L}{6} \ \ のあたり$
$で、確率 \ |\varphi _n(x)|^2\Delta \ x \ が極大になることがわかります。$
$位置の期待値 \ \langle x \rangle \ は$
\begin{eqnarray*}
\langle x \rangle &=&\int _{-\infty}^{+\infty}x |\varphi _n(x)|^2dx\\
&=&\int _0^L x\ \cfrac{2}{L}\sin ^2 \cfrac{n\pi}{L}xdx\\
&=&\cfrac{1}{L}\int _0^L x(1-\cos \cfrac{2n\pi}{L}x)dx\\
&=&\cfrac{1}{L}\Bigl[x(x-\cfrac{L}{2n\pi}\sin \cfrac{2n\pi}{L}x)\Bigr]_0^L-
\cfrac{1}{L}\int _0^L (x-\cfrac{L}{2n\pi}\sin \cfrac{2n\pi}{L}x)dx\\
&=&L-\cfrac{1}{L}\Bigl[\cfrac{x^2}{2}+(\cfrac{L}{2n\pi})^2 \cos \cfrac{2n\pi}{L}x\Bigr]_0^L\\
&=&L-\cfrac{1}{L}\Bigl\{\cfrac{L^2}{2}+(\cfrac{L}{2n\pi})^2 -(\cfrac{L}{2n\pi})^2 \Bigr\}\\
&=&\cfrac{L}{2}\\
\end{eqnarray*}
$となって、井戸の中央になります。$
$(4)\ \ 直交性$
$任意の2つの波動関数\ \ \varphi _m,\ \varphi_n について$
\[\langle \varphi_m , \varphi _n \rangle =\int _0 ^L \varphi_m ^* \varphi_n dx=\cfrac{2}{L}\int _0^L \sin \cfrac{m\pi}{L}x \sin \cfrac{n\pi}{L}xdx=
\left\{ \begin{array}{l}
0 \hspace{3em} (m \neq n )\\
1 \hspace{3em} (m =n )\\
\end{array} \right.
\]
$ですから、\{\varphi _n\}は完全正規直交系となります。$
量子力学メニュー に戻る
メインメニュー に戻る