2次曲線の極方程式
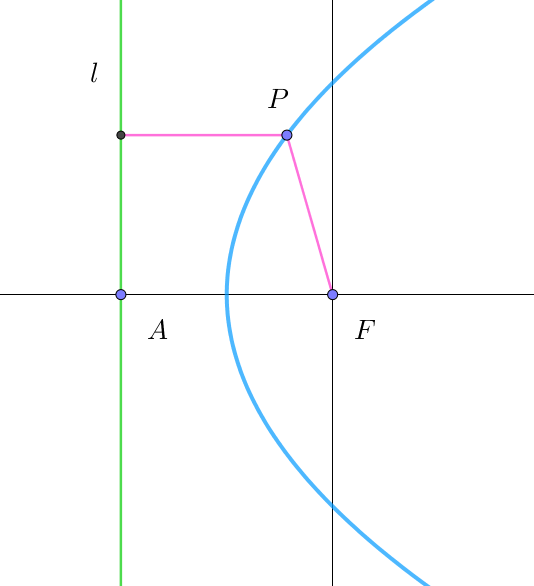
$2次曲線の焦点の \ 1\ つを極とし、極座標が \ (d,\ 0)\ である点を \ A、OA\ 方向の半直線を始線とし、始線に垂直で、$
$点 \ A\ を通る直線 l\ を準線とする。$
$点P(r,\ \theta)\ から準線 \ l\ に下ろした垂線を \ PQ\ とするとき$
$\qquad OP=ePQ \quad (e\ は離心率)$
$となる点 \ P\ の極方程式を求めてみましょう。$
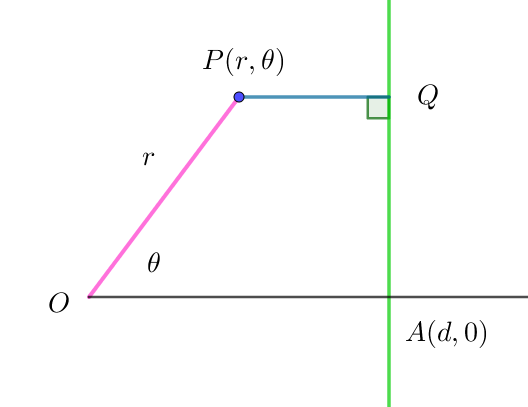
$(1)\ \ 点\ A\ が始点 \ O\ (焦点)の右側にある場合$
$\quad OP=ePQ \quad より \quad r=e(d-r\cos \theta)$
$\quad r=\cfrac{ed}{1+e\cos \theta}$
$\quad ed=l \quad とおくと \quad r=\cfrac{l}{1+e\cos \theta}$
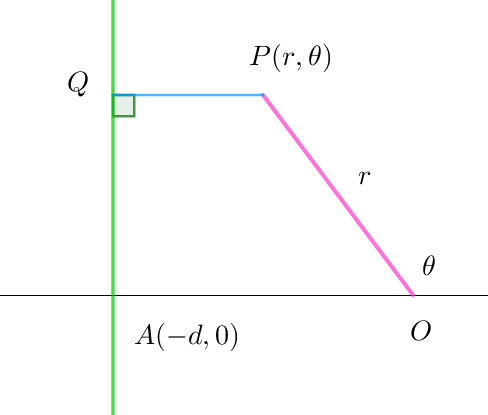
$(2)\ \ 点 \ A\ が始点 \ O\ (焦点)の左側にある場合$
$\quad OP=ePQ \quad より \quad r=e(r\cos \theta +d)$
$\quad r=\cfrac{ed}{1-e\cos \theta}$
$\quad ed=l \quad とおくと \quad r=\cfrac{l}{1-e\cos \theta}$
$\quad このように、始点 \ O\ となる焦点と準線の位置関係により$
$\quad r=\cfrac{l}{1+e\cos \theta} \quad あるいは \quad r=\cfrac{l}{1-e\cos \theta} \quad と表されます。$
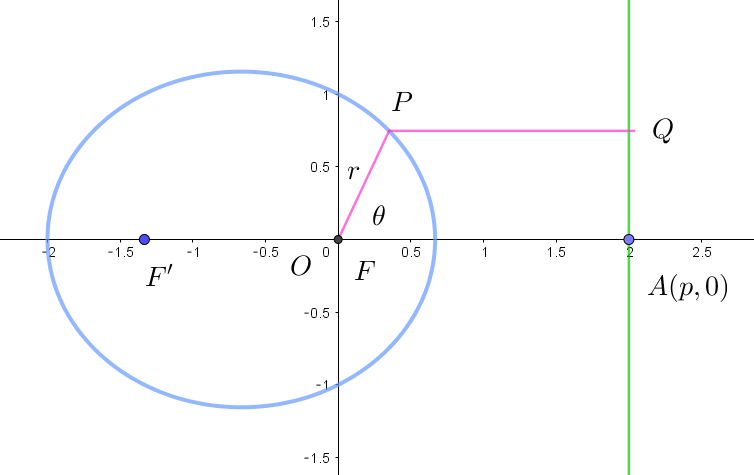
$例1 \quad r=\cfrac{2}{2+\cos \theta}$
$\quad r=\cfrac{1}{1+\dfrac{1}{2}\cos \theta} \quad と変形すると$
(i)$\ \ e=\cfrac{1}{2} \quad だから これは楕円を表します。$
(ii)$\ \ \cos \theta \quad の符号が正だから準線は始点 \ O\ (焦点)の右側にあります。$
(iii)$\ \ 分子=1 \quad より \quad ed=1 \qquad \therefore d=\cfrac{1}{e}=2$
(iv)$\ \ 焦点 \ F\ を始点とするから \ xy\ 座標軸の原点は \ x\ 軸方向に \ -ae \ 平行移動される。$
$\qquad よって準線について \quad d+ae=\cfrac{a}{e} \qquad 2+\cfrac{1}{2}a=2a \qquad a=\cfrac{4}{3}$
(v)$\ \ 離心率 \ e\ について$
$\qquad e=\cfrac{\sqrt{a^2-b^2}}{a}=\cfrac{1}{2} \quad より\quad a^2-b^2=\cfrac{a^2}{4} \qquad b^2=\cfrac{3}{4}a^2=\cfrac{3}{4} \times (\cfrac{4}{3})^2=\cfrac{4}{3}$
$\quad xy\ 座標軸の原点は \ x\ 軸方向に \quad -ae=-\cfrac{4}{3} \times \cfrac{1}{2}=-\cfrac{2}{3} \quad 平行移動されるから$
$\qquad xy\ 表示では \qquad \cfrac{(x+\dfrac{2}{3})^2}{\dfrac{16}{9}}+\cfrac{y^2}{\dfrac{4}{3}}=1$
 $(別解)$
$(別解)$
$\quad r(2+\cos \theta)=2 \quad より \quad 2r+r\cos \theta=2$
$\quad 2\sqrt{x^2+y^2}+x=2 \qquad \quad 4(x^2+y^2)=(2-x)^2$
$\quad 3x^2+4x+4y^2=4 \qquad \therefore \ \ \cfrac{(x+\dfrac{2}{3})^2}{\dfrac{16}{9}}+\cfrac{y^2}{\dfrac{4}{3}}=1$
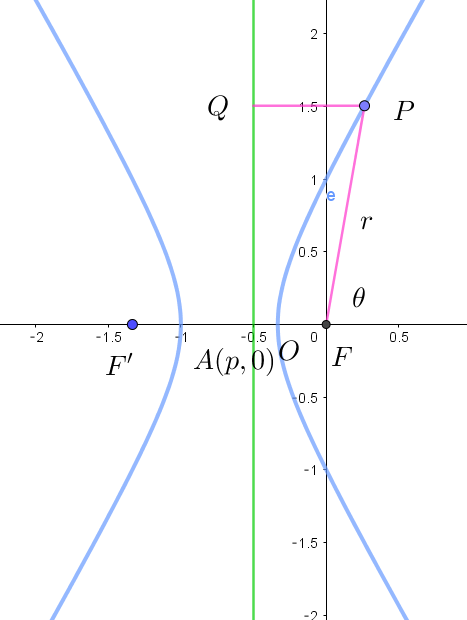
$例2 \quad r=\cfrac{1}{1-2\cos \theta}$
(i)$\ \ e=2 \quad だから これは双曲線を表します。$
(ii)$\ \ \cos \theta \quad の符号が負だから準線は始点 \ O\ (焦点)の左側にあります。$
(iii)$\ \ 分子=1 \quad より \quad ed=1 \quad \therefore \ \ d=\cfrac{1}{e}=\cfrac{1}{2}$
(iv)$\ \ 焦点 \ F\ を始点とするから \ xy\ 座標軸の原点は \ x\ 軸方向に \ -ae \ 平行移動される。$
$\qquad よって準線について \quad -d+ae=\cfrac{a}{e} \quad -\cfrac{1}{2}+2a=\cfrac{a}{2} \qquad a=\cfrac{1}{3}$
(v)$\ \ 離心率 \ e\ について$
$\qquad e=\cfrac{\sqrt{a^2+b^2}}{a}=2 \quad より \quad a^2+b^2=4a^2 \qquad b^2=3a^2=3 \times (\cfrac{1}{3})^2=\cfrac{1}{3}$
$\quad xy\ 座標軸の原点は \ x\ 軸方向に \quad -ae=-\cfrac{1}{3} \times 2=-\cfrac{2}{3} \quad 平行移動されるから$
$\qquad xy\ 表示では \qquad \cfrac{(x+\dfrac{2}{3})^2}{\dfrac{1}{9}}-\cfrac{y^2}{\dfrac{1}{3}}=1$
 $(別解)$
$(別解)$
$\quad r(1-2\cos \theta)=1 \quad より \quad r-2r\cos \theta=1$
$\quad \sqrt{x^2+y^2}-2x=1 \qquad x^2+y^2=(2x+1)^2$
$\quad 3x^2+4x-y^2=-1 \qquad \therefore \ \ \cfrac{(x+\dfrac{2}{3})^2}{\dfrac{1}{9}}-\cfrac{y^2}{\dfrac{1}{3}}=1$
$例3 \quad r=\cfrac{1}{1-\cos \theta}$
(i)$\ \ e=1 \quad だから これは放物線を表します。$
(ii)$\ \ \cos \theta \ \ の符号が負だから準線は始点 \ O(焦点)の左側にあります。$
(iii)$\ \ 分子=1 \quad より \quad ed=1 \quad \therefore \ \ d=\cfrac{1}{e}=1 \quad よって 点 \ A\ は \ A(-1,\ 0)$
(iv)$\ \ FA=2p \quad だから \quad p=\cfrac{1}{2}$
(v)$\ \ 焦点 \ F\ を始点とするから \ xy\ 座標軸の原点は \ x\ 軸方向に \ -p \ 平行移動される。$
$\qquad xy\ 表示では \quad y^2=4 \times \cfrac{1}{2} (x+\cfrac{1}{2}) \qquad \therefore \ \ y^2=2(x+\cfrac{1}{2})$
 $(別解)$
$(別解)$
$\quad r(1-\cos \theta)=1 \quad より \quad r-r\cos \theta=1$
$\quad \sqrt{x^2+y^2}-x=1 \qquad x^2+y^2=(x+1)^2$
$\quad y^2=2x+1 \qquad \therefore \ \ y^2=4 \times \cfrac{1}{2}(x+\cfrac{1}{2})$
$焦点に関する性質を調べましょう。$
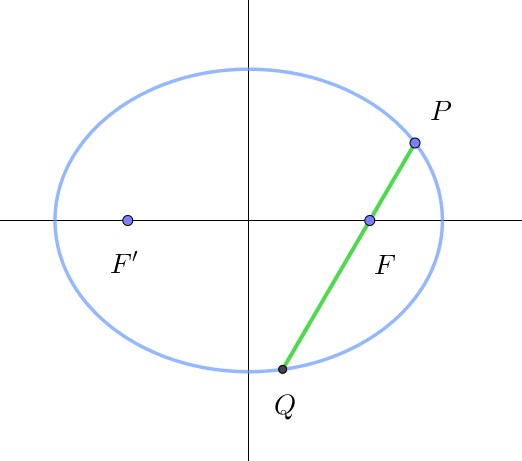
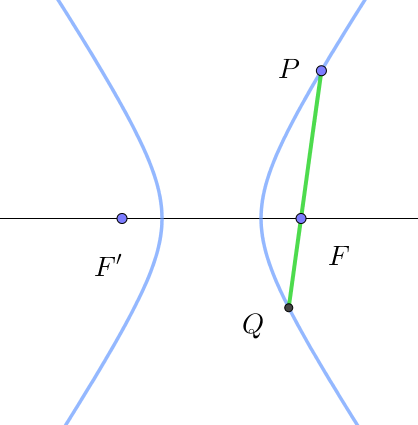
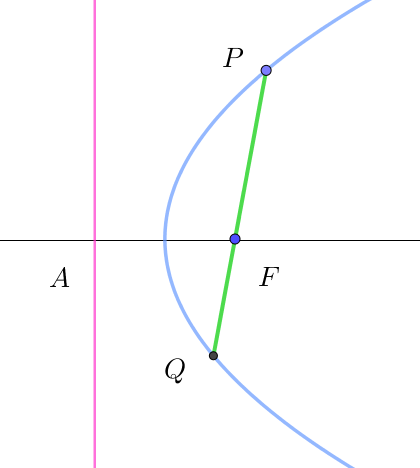
$例4 \quad 2\ 次曲線の \ 1\ つの焦点 \ F\ を通る弦を \ PQ\ とするとき、\cfrac{1}{FP}+\cfrac{1}{FQ} \ \ は一定である。$
$(証明)$
$\quad 2\ 次曲線の焦点 \ F\ を始点とする極方程式は$
$\qquad r=\cfrac{l}{1+e\cos \theta} \quad と表される。$
$\quad 曲線上の任意の点を \ P(r,\ \theta) \ \ とすると、Q(r,\ \pi+\theta)\ \ とおけるから$
$\qquad \cfrac{1}{FP}+\cfrac{1}{FQ}=\cfrac{1+e\cos \theta}{l}+\cfrac{1+e\cos (\pi+\theta)}{l} =\cfrac{1+e\cos \theta}{l}+\cfrac{1-e\cos \theta}{l}=\cfrac{2}{l}\quad (一定)$
2次曲線メニュー に戻る
メインメニュー に戻る