$\pi$ の近似分数表示
1 連分数
$実数xに対し、その整数部分を [x]=q_1 とすると \hspace{2em} x=q_1+r_1 \quad (0 \leqq r_1 < 1) $
$\hspace{2em} r_1\neq 0 ならば \cfrac{1}{r_1}=x_2 > 1 だから$
$\hspace{2em} [x_2]=q_2 として \hspace{2em} x_2=q_2+r_2 \quad (0 \leqq r_2 < 1) とかける。$
これを繰り返して
$\hspace{2em} x=q_1+r_1=q_1+\cfrac{1}{x_2}=q_1+\cfrac{1}{q_2+r_2}=q_1+\cfrac{1}{q_2+\cfrac{1}{x_3}}=\cdots $
のように表わせますが、これを実数の連分数表示といいます。
このままでは多くの行数を使いますので、簡単に
$\hspace{2em} q_1+\cfrac{1}{q_2}{{} \atop +} \cfrac{1}{q_3}{{} \atop {+ \cdots }} のように表します。(+記号の位置に注意!!)$
2 $\pi$ の連分数表示
$\quad \pi$=3.141592653589793238462643383279 としてパソコンで計算すると
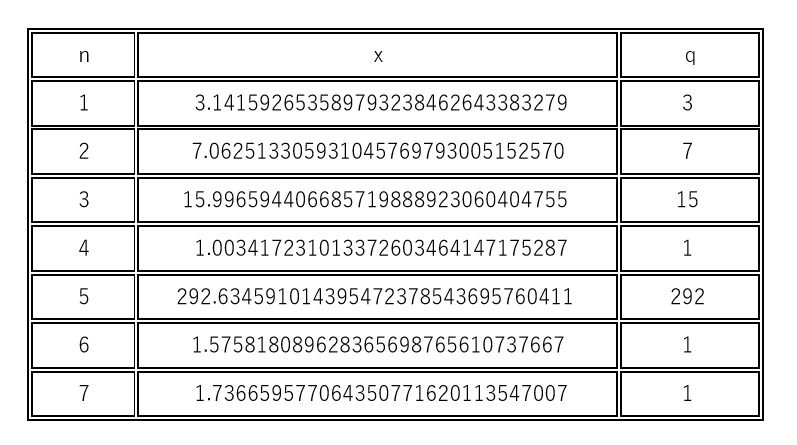
したがって
$\hspace{4em} \pi=3+\cfrac{1}{7}{{} \atop +} \cfrac{1}{15}{{} \atop +} \cfrac{1}{1}{{} \atop +} \cfrac{1}{292}{{} \atop +} \cfrac{1}{1}{{} \atop +} \cfrac{1}{1}{{} \atop {+ \cdots }} $
となります。
3 近似分数表示
$\hspace{2em}連分数 x=q_1+\cfrac{1}{q_2}{{} \atop +} \cfrac{1}{q_3}{{} \atop {+ \cdots }} の第n項までとった$
$\hspace{3em} x_n=q_1+\cfrac{1}{q_2} { { } \atop +} \cfrac{1}{q_3}{{} \atop {+ \cdots + }} \cfrac{1}{q_n} =\cfrac{P_n}{Q_n}$
$\hspace{2em} を x の第n次近似分数といいます。$
性質 (証明は省略します)
$(1)\ 漸化式$
\[p_n=a_np_{n-1}+p_{n-2} \hspace{20em} \atopwithdelims\{. q_n=a_nq_{n-1}+q_{n-2} \hspace{20em}\]
$(2)\quad p_n と q_nはともに単調増加$
$(3)\quad \cfrac{p_n}{q_n} はすべて既約分数 $
$(4)\quad \cfrac{p_0}{q_0} < \cfrac{p_2}{q_2} < \cdots < x < \cdots < \cfrac{p_3}{q_3} < \cfrac{p_1}{q_1} \hspace{12em}$
4 $\pi$ の近似分数
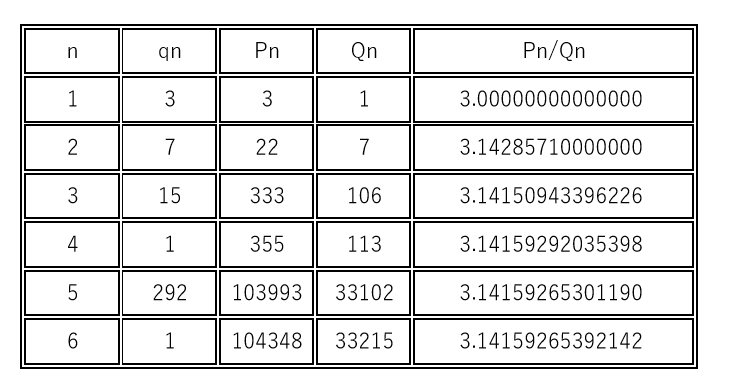
$\hspace{1em} n=2 \ の \cfrac{22}{7} や n=4 \ の \cfrac{355}{113} は有名な分数です。$
$さすがに、次の\ \cfrac{103993}{33102} は覚えようがありません。$
円周率 $π$ の話 に戻る
メインメニュー に戻る