大阪大学(理系) 2023年　問題4


$a,\ b\ を \ a^2+b^2 > 1\ \ かつ \ \ b \ne 0 \ \ をみたす実数の定数とする。座標空間の点 \ A(a,\ 0,\ b) \ と点 \ P(x,\ y,\ 0)\ をとる。$
$点 \ O(0,\ 0,\ 0)\ を通り直線 \ AP\ と垂直な平面を \ \alpha \ とし、平面 \ \alpha \ と直線 \ AP\ との交点を \ Q\ とする。$
$(1)\ \ (\vec{AP}\cdot \vec{AO})^2=|\vec{AP}|^2 |\vec{AQ}|^2 \ \ が成り立つことを示せ。$
$(2)\ \ |\vec{OQ}|=1 \ \ をみたすように点 \ P(x,\ y,\ 0)\ が \ xy\ 平面上を動くとき、点 \ P\ の軌跡を求めよ。$


(1)

　

$\vec{AP}\ と \ \vec{AO}\ のなす角を \ \theta \ とすると$

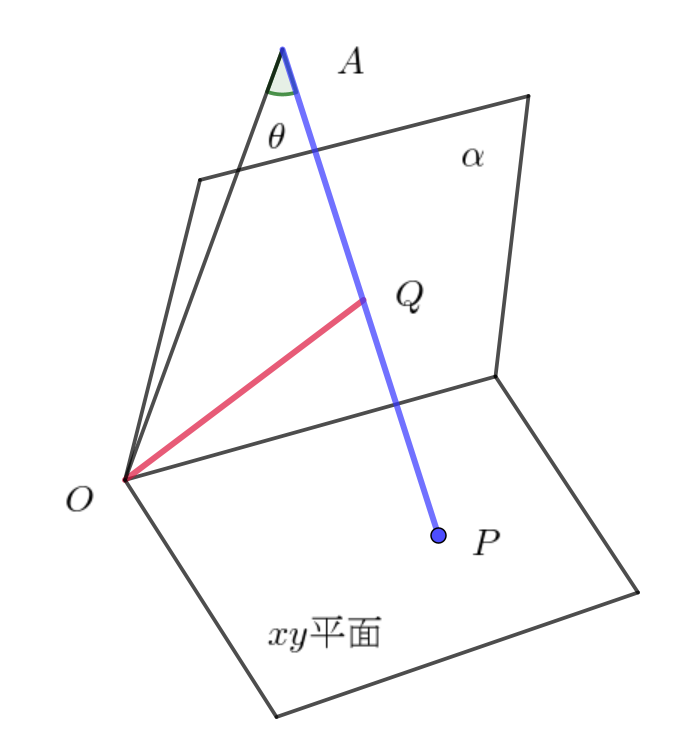
$3\ 点 \ A,\ Q,\ P\ は一直線上にあるから \ \theta \ は$

$\vec{AQ}\ と \ \vec{AO}\ のなす角でもある。$

$AQ\ は平面 \ \alpha \ に垂直だから \ AQ \ は \ \alpha \ 上の$

$線分 \ OQ\ とも垂直である。$

$よって \quad \triangle OAQ \ は \ \angle OQA=90°\ の直角三角形である。$

$\vec{AP}\cdot \vec{AO}=|\vec{AP}||\vec{AO}|\cos \theta =|\vec{AP}||\vec{AQ}|$

$\therefore \ \ (\vec{AP}\cdot \vec{AO})^2=|\vec{AP}|^2 |\vec{AQ}|^2$


(2)


$|\vec{OQ}|=1 \quad より \quad AQ^2=OA^2-OQ^2=a^2+b^2-1 $

$\vec{AP}=\vec{OP}-\vec{OA}=(x,\ y,\ 0)-(a,\ 0,\ b)=(x-a,\ y,\ -b)$

$\vec{AO}=-\vec{OA}=-(a,\ 0,\ b)=(-a,\ 0,\ -b)$

$よって \quad \vec{AP}\cdot \vec{AO} =-a(x-a)-b(-b)=-ax+a^2+b^2$

$(1)より \quad (\vec{AP}\cdot \vec{AO})^2=|\vec{AP}|^2 |\vec{AQ}|^2 \quad に代入して$

$(-ax+a^2+b^2)^2=\{(x-a)^2+y^2+(-b)^2\}(a^2+b^2-1)$

$a^2x^2-2a(a^2+b^2)x+(a^2+b^2)^2=(a^2+b^2-1)x^2-2a(a^2+b^2-1)x+(a^2+b^2-1)y^2+(a^2+b^2)(a^2+b^2-1)$

$(b^2-1)x^2+2ax+(a^2+b^2-1)y^2-(a^2+b^2)=0 $

(i)$\ \ b \ne \pm 1 \quad のとき$

$ \quad (b^2-1)\big\{x^2+ \cfrac{2a}{b^2-1}x\big\} +(a^2+b^2-1)y^2=(a^2+b^2)$

$ \quad (b^2-1)\big\{\big(x+ \cfrac{a}{b^2-1}\big)^2 -\big(\cfrac{a}{b^2-1}\big)^2\big\} +(a^2+b^2-1)y^2=(a^2+b^2)$

$ \quad (b^2-1)\big(x+ \cfrac{a}{b^2-1}\big)^2 +(a^2+b^2-1)y^2=(a^2+b^2)+ \cfrac{a^2}{b^2-1}$

$ \quad (b^2-1)\big(x+ \cfrac{a}{b^2-1}\big)^2 +(a^2+b^2-1)y^2=\cfrac{b^2(a^2+b^2-1)}{b^2-1}$

$ \quad \cfrac{\big(x+ \dfrac{a}{b^2-1}\big)^2}{a^2+b^2-1} + \cfrac{y^2}{b^2-1}=\cfrac{b^2}{(b^2-1)^2}$

$ \quad (ア) \quad b >1 ,\ \ b < -1 \quad のとき \quad 　b^2-1> 0 ,\ \ a^2+b^2-1>0 \quad だから \ \ 楕円を表す。$

$ \quad (イ) \quad -1 < b <1 \quad のとき \quad 　　b^2-1< 0 ,\ \ a^2+b^2-1>0 \quad だから \ \ 双曲線を表す。$

(ii)$\ \ b =\pm 1 \quad のとき$

$ \quad 2ax+a^2y^2-a^2-1=0 $

$ \quad (ウ) \quad a \ne 0 \quad のとき \quad 　y^2=-\cfrac{2}{a}x +\cfrac{a^1+1}{a^2} \quad だから \ \ 放物線を表す。$

$ \quad (エ） \quad a =0 \quad のとき \quad 直角三角形OAQ \ は斜辺 \ OA=1,\ \ OQ=1 \quad だから不合理$

$以上より点 \ P\ の軌跡は$

$(ア) \quad b >1 ,\ \ b < -1 \quad のとき \quad 楕円$

$(イ) \quad -1 < b <1 \ \ (b \ne 0) \quad のとき \quad 双曲線$

$(ウ) \quad a \ne 0 , \ \ b=\pm 1 \quad のとき \quad 放物線$


ページの先頭へ↑




メインメニュー　に戻る