大阪大学(理系) 2021年 問題1
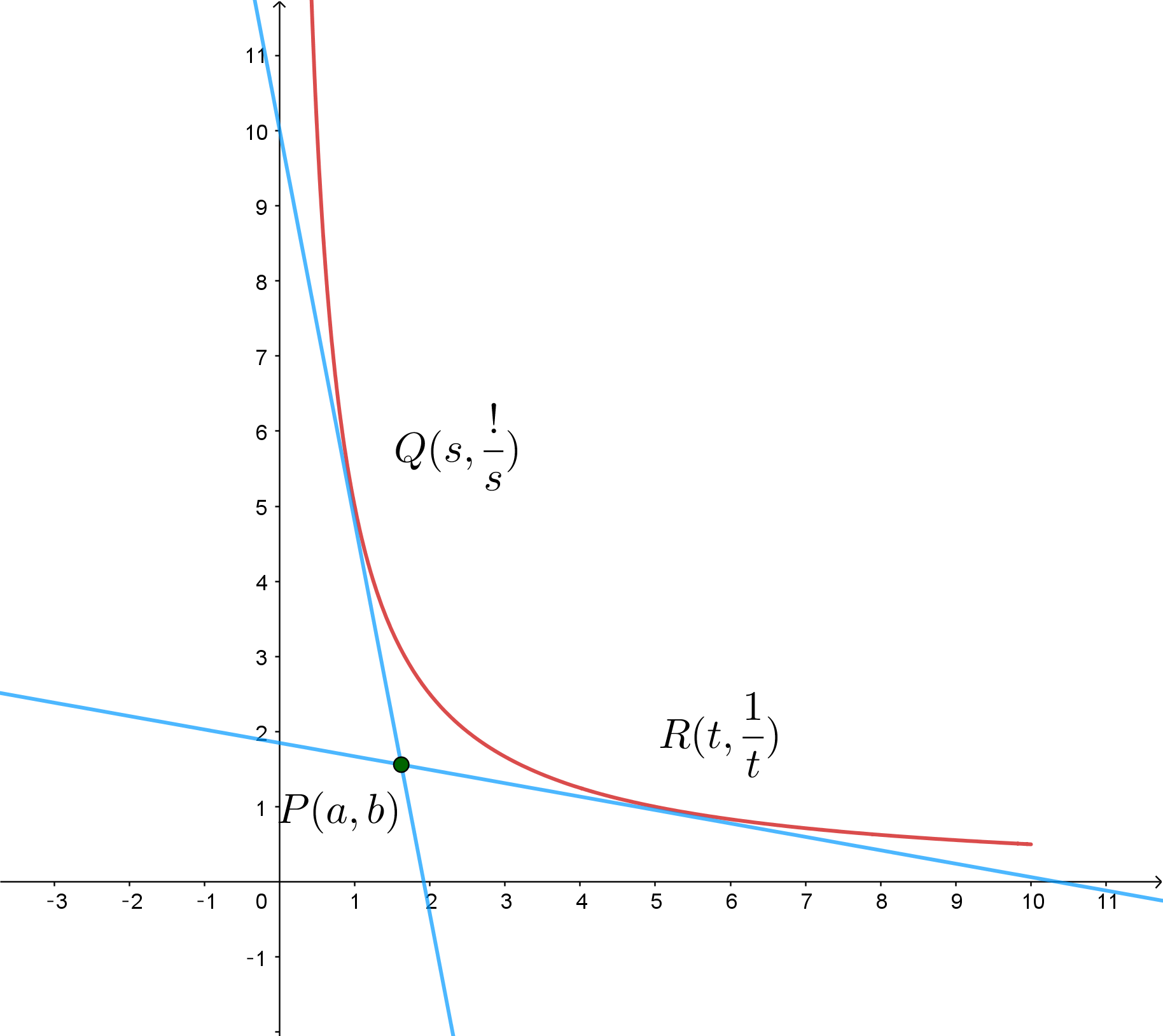
$a,\ b\ を \ ab < 1 \ をみたす正の実数とする。xy\ 平面上の点 \ P(a,\ b)\ から、曲線 \ y=\cfrac{1}{x} \ \ (x > 0)\ に \ 2\ 本の$
$接線を引き、その接点を \ Q(s,\ \cfrac{1}{s}),\ \ R(t,\ \cfrac{1}{t})\ とする。ただし、s < t \ \ とする。$
$(1)\ \ s\ および \ t\ を \ a,\ b\ を用いて表せ。$
$(2)\ \ 点 \ P(a,\ b)\ が曲線 \ y=\cfrac{9}{4}-3x^2\ \ 上の \ \ x > 0,\ \ y > 0\ \ をみたす部分を動くとき、\cfrac{t}{s}\ \ の最小値と$
$\qquad そのときの \ a,\ b\ の値を求めよ。$
$(解説)$
$(1)\ \ 曲線外の点から引いた接線の方程式と接点の座標の求め方は定石どおりです。$
$(2)\ \ \cfrac{t}{s}\ \ を \ a\ の関数として表し、微分して増減を調べればいいのですが、まともにやると計算が大変です。$
$\qquad 置き換えた方法を別解としました。$
(1)
$y=\cfrac{1}{x} \quad より \qquad y'=-\cfrac{1}{x^2}$
$曲線上の点 \ (u,\ \cfrac{1}{u})\ における接線は$
$\quad y=-\cfrac{1}{u^2}(x-u)+\cfrac{1}{u} \qquad y=-\cfrac{1}{u^2}x+\cfrac{2}{u}$
$これが \quad P(a,\ b)\ を通るから \qquad b=-\cfrac{1}{u^2}a+\cfrac{2}{u}$
$bu^2-2u+a=0 \quad この解は \quad u=\cfrac{1 \pm \sqrt{1-ab}}{b}$
$これが \ \ s,\ \ t \ \ であり、s < t \quad だから$
$\qquad s=\cfrac{1 - \sqrt{1-ab}}{b},\qquad t=\cfrac{1 + \sqrt{1-ab}}{b}$
(2)
$点 \ P(a,\ b)\ は \ \ y=\cfrac{9}{4}-3x^2 \ \ 上にあるから \quad b=\cfrac{9}{4}-3a^2$
$a > 0,\ \ b > 0 \quad だから \quad \cfrac{9}{4}-3a^2> 0 \quad よって \quad 0 < a < \cfrac{\sqrt{3}}{2}$
\begin{eqnarray*} \cfrac{t}{s} &=&\cfrac{1 + \sqrt{1-ab}}{b} \times \cfrac{b}{1 - \sqrt{1-ab}}\\ \\ &=&\cfrac{1+\sqrt{1-a(\dfrac{9}{4}-3a^2)}}{1-\sqrt{1-a(\dfrac{9}{4}-3a^2)}}\\ \\ &=&\cfrac{2+\sqrt{4-9a+12a^3}}{2-\sqrt{4-9a+12a^3}}\\ \end{eqnarray*}
$\qquad f(a)=\cfrac{2+\sqrt{4-9a+12a^3}}{2-\sqrt{4-9a+12a^3}} \quad とおくと$
\begin{eqnarray*} f'(a) &=&\cfrac{\dfrac{-9+36a^2}{2\sqrt{4-9a+12a^3}} \times (2-\sqrt{4-9a+12a^3})- (2+\sqrt{4-9a+12a^3}) \times \dfrac{-9+36a^2}{-2\sqrt{4-9a+12a^3}}}{(2-\sqrt{4-9a+12a^3})^2}\\ \\ &=&\cfrac{(-9+36a^2)(2-\sqrt{4-9a+12a^3}) + (-9+36a^2)(2+\sqrt{4-9a+12a^3})}{2(2-\sqrt{4-9a+12a^3})^2 \sqrt{4-9a+12a^3}}\\ \\ &=&\cfrac{18(4a^2-1)}{(2-\sqrt{4-9a+12a^3})^2 \sqrt{4-9a+12a^3}}\\ \end{eqnarray*}
$\qquad f'(a)=0 \quad より \quad a=\cfrac{1}{2}$
\[ \begin{array}{c||c|c|c|c|c} \hline a& 0 & \cdots & \dfrac{1}{2} & \cdots & \dfrac{\sqrt{3}}{2}\\ \hline f'(a)& & - & 0 & + & \\ \hline f(a)& & \searrow & 極小 & \nearrow & \\ \hline \end{array} \]

$\qquad a \longrightarrow +0 \quad のとき \quad f(a) \longrightarrow +\infty$
$\qquad a \longrightarrow \cfrac{\sqrt{3}}{2} -0 \quad のとき \quad f(a) \longrightarrow +\infty$
$f(a)\ は \ a=\cfrac{1}{2}\ で極小かつ最小となり$
$最小値は \quad f(\cfrac{1}{2})=\cfrac{2+\sqrt{4-\dfrac{9}{2}+\dfrac{3}{2}}}{2-\sqrt{4-\dfrac{9}{2}+\dfrac{3}{2}}}=\dfrac{2+1}{2-1}=3$
$このとき \quad b=\cfrac{9}{4}-3 \times \cfrac{1}{4}=\cfrac{3}{2}$
$(別解)$
$\cfrac{t}{s}=\cfrac{2+\sqrt{4-9a+12a^3}}{2-\sqrt{4-9a+12a^3}} \quad において$
$\quad v(a)=4-9a+12a^3 , \qquad u=\sqrt{4-9a+12a^3} \quad とおくと $
$\quad v'(a)=-9+36a^2=9(4a^2-1)$
$\quad v'(a)=0 \quad より \quad a^2=\cfrac{1}{4} \quad \therefore \ \ a=\cfrac{1}{2}$
\[
\begin{array}{c||c|c|c|c|c}
\hline
a& 0 & \cdots & \dfrac{1}{2} & \cdots & \dfrac{\sqrt{3}}{2}\\
\hline
v'(a)& & - & 0 & + & \\
\hline
v(a)& 4 & \searrow & 極小 & \nearrow & 4\\
\hline
\end{array}
\]
$v(a) \ は \ \ a=\cfrac{1}{2}\ で極小かつ最小となり、最小値は \quad v(\cfrac{1}{2})=4-\cfrac{9}{2}+12 \times \cfrac{1}{8}=1$
$\quad v(0)=4,\qquad v(\cfrac{\sqrt{3}}{2})=4-\cfrac{9\sqrt{3}}{2}+12 \times \cfrac{3\sqrt{3}}{8}=4$
$よって \quad 1 \leqq v(a) < 4 \quad だから \quad 1 \leqq u <2$
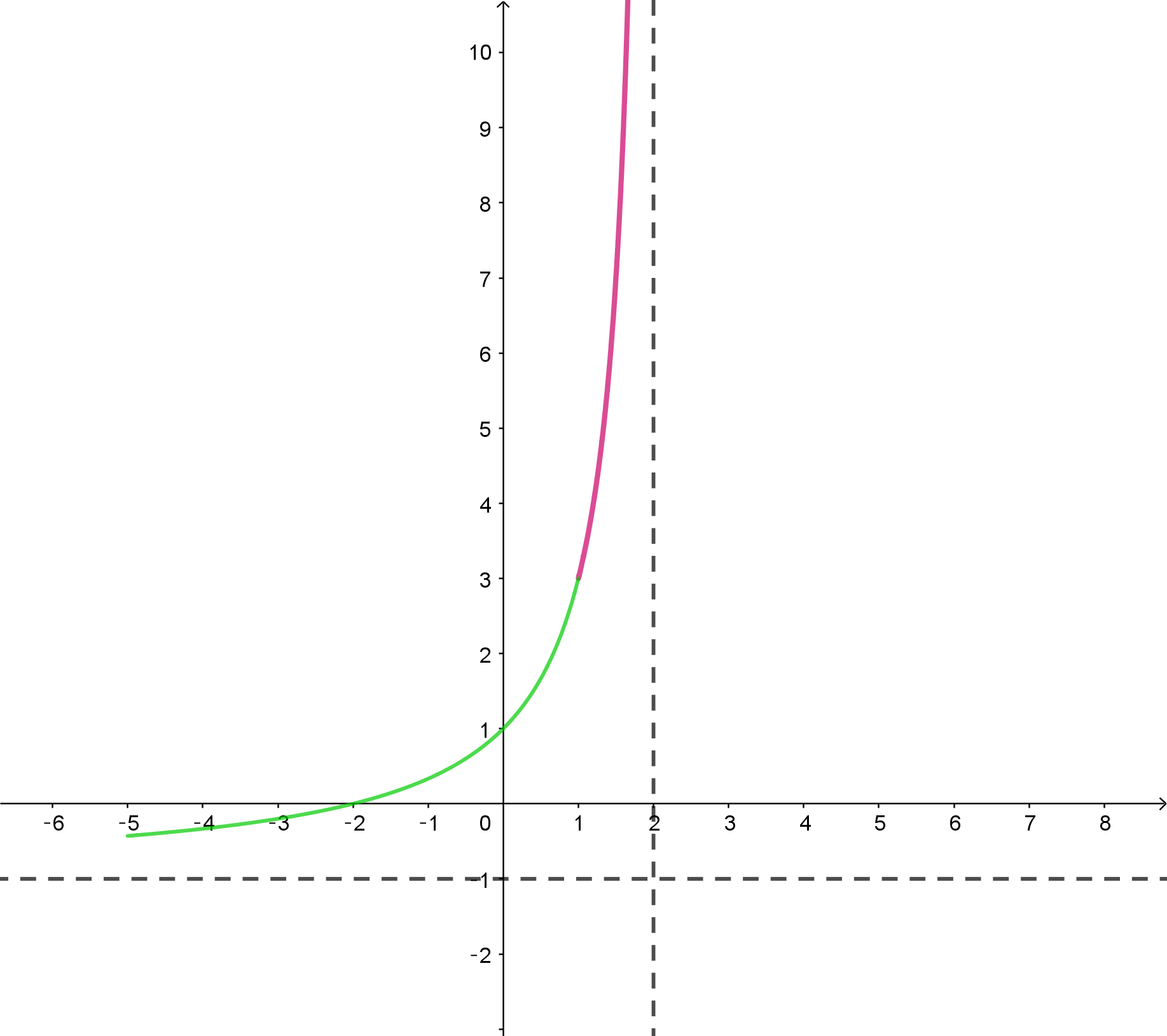
$\cfrac{t}{s}=\cfrac{2+u}{2-u}=g(u) \quad とおくと$
$\quad g(u)=-1-\cfrac{4}{u-2} $
$このグラフは右図のとおりで、u=1\ のとき \ \ 最小値 \ 3\ をとる。$
$このとき、a=\cfrac{1}{2} \quad である。$
メインメニュー に戻る