岡山大学(理系) 2023年 問題4
$0 < x < y \ \ とする。平行四辺形 \ ABCD\ において、辺 \ AB\ の長さを \ x、辺 \ BC\ の長さを \ y,\ \angle ABC=2\theta $
$( 0 < \theta < \cfrac{\pi}{2})\ \ とする。平行四辺形 \ ABCD\ の内角 \ A,\ B,\ C,\ D\ を \ 2\ 等分する直線をそれぞれ \ l_A,\ l_B,\ l_C,\ l_D$
$とし、l_A \ と \ l_B\ の交点を \ E,\ l_B\ と \ l_C\ の交点を \ F,\ l_C \ と \ l_D\ の交点を \ G,\ l_D \ と \ l_A\ の交点を \ H\ とする。$
$平行四辺形 \ ABCD\ と四角形 \ EFGH\ が重なる部分の面積を \ S\ とする。以下の問いに答えよ。$
$(1)\ \ \angle FEH \ を求めよ。$
$(2)\ \ 線分 \ AE\ および線分 \ AH\ の長さを求めよ。$
$(3)\ \ 点 \ H\ が平行四辺形 \ ABCD\ の外部にあるような、x,\ y\ の条件を求めよ。$
$(4)\ \ S\ を求めよ。$
(1)
$\hspace{8em}点 \ H\ が内部にある場合 \hspace{13em}点 \ H\ が外部にある場合$
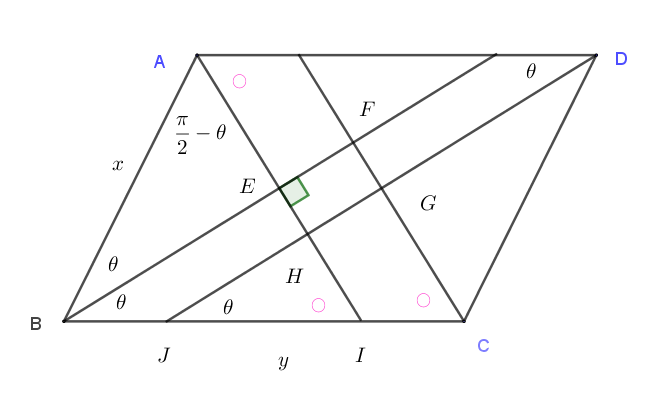
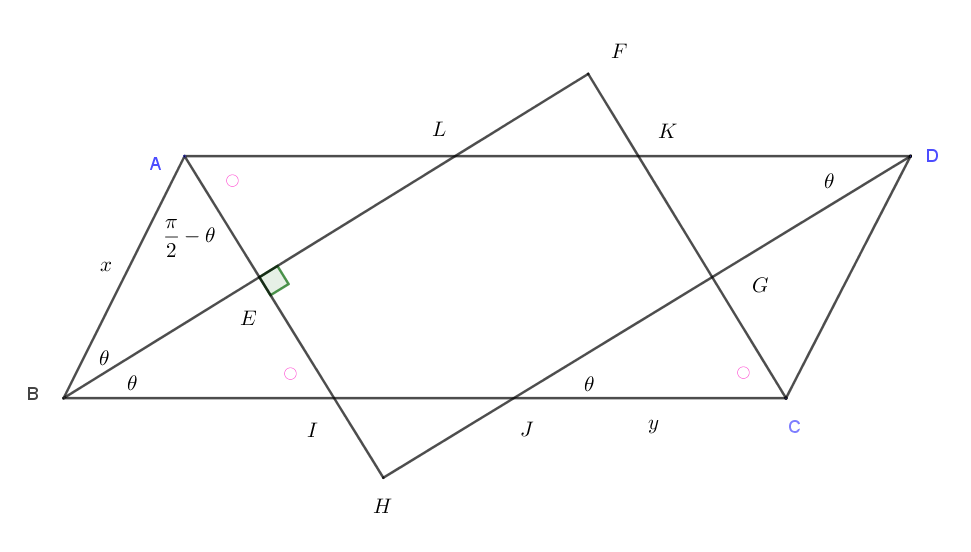
$上図のように、l_A,\ l_D\ と辺 \ BC\ の交点をそれぞれ \ I,\ J\ とおく。$
$\triangle ABE\ \ において \ \ \angle ABE=\theta,\quad \angle BAD=\pi -\angle ABC=\pi -2\theta \quad だから \quad \angle BAE=\cfrac{\pi}{2}-\theta$
$\quad \angle AEB=\pi -\angle ABE - \angle BAE=\pi - \theta - (\cfrac{\pi}{2} -\theta)=\cfrac{\pi}{2}$
$\quad よって \quad \angle FEH=\angle AEB=\cfrac{\pi}{2}$
(2)
$\triangle ADH \ \ において \ \ \angle ADH=\theta,\quad \angle DAH=\angle BAE=\cfrac{\pi}{2}-\theta$
$\quad よって \quad \angle AHD=\pi -\angle ADH - \angle DAH=\pi -\theta - (\cfrac{\pi}{2}-\theta) =\cfrac{\pi}{2}$
$\triangle CDG \ \ において \ \ \angle CDG=\theta, \quad \angle DCG=\angle BCG=\cfrac{\pi}{2}-\theta$
$\quad よって \quad \angle FGH=\angle DGC= \pi -\angle CDG - \angle DCG=\pi -\theta - (\cfrac{\pi}{2}-\theta) =\cfrac{\pi}{2}$
$これらのことから \ \ \angle EFG=\cfrac{\pi}{2} \ \ となり、四角形 \ EFGH\ は長方形である。$
$\triangle ABE \ \ において \quad AE=AB\sin \theta =x\sin \theta $
$\triangle ADH \ \ において \quad AH=AD\sin \theta =y\sin \theta$
(3)
$AD /\!/ BC \ \ だから \quad \angle AIB=\angle IAD=\cfrac{\pi}{2}-\theta$
$\triangle ABI \ \ において正弦定理をもちいて$
$\quad \cfrac{AI}{\sin 2\theta}=\cfrac{AB}{\sin(\cfrac{\pi}{2}-\theta)} \qquad AI=\cfrac{AB}{\sin(\cfrac{\pi}{2}-\theta)} \times \sin 2\theta =\cfrac{x \sin 2\theta}{\cos \theta}=2x\sin \theta$
$点 \ H\ が平行四辺形 \ ABCD\ の外部にあるときは \quad AH > AI \quad だから$
$\quad y\sin \theta > 2x\sin \theta \qquad \therefore \ \ y > 2x $
(4)
$\triangle ABE \ \ において \quad BE=AB\cos \theta =x\cos \theta$
$\triangle BCF \ \ において \quad BF=BC \cos \theta =y\cos \theta$
$\triangle ADH \ \ において \quad DH=AD \cos \theta =y\cos \theta$
$\triangle CDG \ \ において \quad DG=CD \cos \theta =x\cos \theta$
$BF /\!/ JD \ \ より \quad \angle CJD =\angle CBF=\theta$
$\triangle CDJ \ \ において正弦定理をもちいて$
$\quad \cfrac{DJ}{\sin (\pi -2\theta)}=\cfrac{CD}{\sin \theta} \qquad DJ=\cfrac{CD}{\sin \theta} \times \sin 2\theta =\cfrac{x \sin 2\theta}{\sin \theta}=2x\cos \theta$
$四角形 \ EFGH\ は長方形であるから$
(i)$\ \ y \leqq 2x \quad のとき$
$\quad 点 \ H\ が平行四辺形 \ ABCD\ の内部にあるから平行四辺形 \ ABCD\ と四角形 \ EFGH\ が$
$\quad 重なる部分は長方形\ EFGH$
\begin{eqnarray*} \quad S &=&長方形 \ EFGH\\ \\ &=&EH \times GH\\ \\ &=&(AH -AE) \times (DH -DG)\\ \\ &=&(y\sin \theta - x\sin \theta) \times (y\cos \theta - x\cos \theta)\\ \\ &=&(y-x)^2 \sin \theta \cos \theta\\ \\ &=&\cfrac{1}{2}(y-x)^2\sin 2 \theta \end{eqnarray*}
(ii)$\ \ y > 2x \quad のとき$
$\quad 点 \ H\ が平行四辺形 \ ABCD\ の外部にあるから平行四辺形 \ ABCD\ と四角形 \ EFGH\ が$
$\quad 重なる部分は六角形\ EIJGKL$
\begin{eqnarray*} \quad S &=&六角形 \ EIJGKL\\ \\ &=&長方形 \ EFGH - 2\triangle HIJ \\ \\ &=&長方形 \ EFGH - IH \times JH \\ \\ &=&長方形 \ EFGH - (AH-AI) \times (DH-DJ)\\ \\ &=&\cfrac{1}{2}(y-x)^2\sin 2 \theta - (y\sin \theta -2x\sin \theta)(y\cos \theta -2x\cos \theta)\\ \\ &=&\cfrac{1}{2}(y-x)^2\sin 2 \theta - (y-2x)^2\sin \theta \cos \theta \\ \\ &=&\cfrac{1}{2}(y-x)^2\sin 2 \theta - \cfrac{1}{2}(y-2x)^2\sin 2\theta \\ \\ &=&\cfrac{1}{2}x(2y-3x)\sin 2\theta \end{eqnarray*}
メインメニュー に戻る