岡山大学(理系) 2021年 問題4
$正の整数 \ n\ に対して、関数 \ f(x)=x^{2n}\ を考える。t > 0 \ に対して、曲線 \ y=f(x)\ 上の \ 3\ 点 \ A(-t,\ f(-t)),$
$O(0,\ 0),\ B(t, f(t))\ を通る円の中心を \ (p(t),\ q(t)),半径を \ r(t)\ とする。このとき、以下の問いに答えよ。$
\[(1)\ \ 極限 \ \ \lim _{t \rightarrow +0} p(t),\ \ \lim _{t \rightarrow +0} q(t),\ \ \lim _{t \rightarrow +0} r(t) \ がすべて収束するとき \ n=1\ であることを示せ。\]
\[\quad また、このとき \ a=\lim _{t \rightarrow +0} p(t),\ \ b=\lim _{t \rightarrow +0} q(t),\ \ c=\lim _{t \rightarrow +0} r(t) \ の値を求めよ。\]
$\qquad (2)\ \ a,\ b,\ c\ を(1)で求めたものとする。このとき、中心 \ (a,\ b),半径 \ c\ の円と放物線 \ y=x^2\ \ および$
$\hspace{3em} 直線 \ x=b \ で囲まれた図形を、x\ 軸の周りに \ 1\ 回転してできる回転体の体積 \ V\ を求めよ。$
$(解説)$
$(1)\ \ p,\ q,\ r\ は図形的に簡単に求められます。発散しないような \ n\ を求めればよいわけです。$
$(2)\ \ くり抜かれた回転体の体積を求めることになります。$
(1)
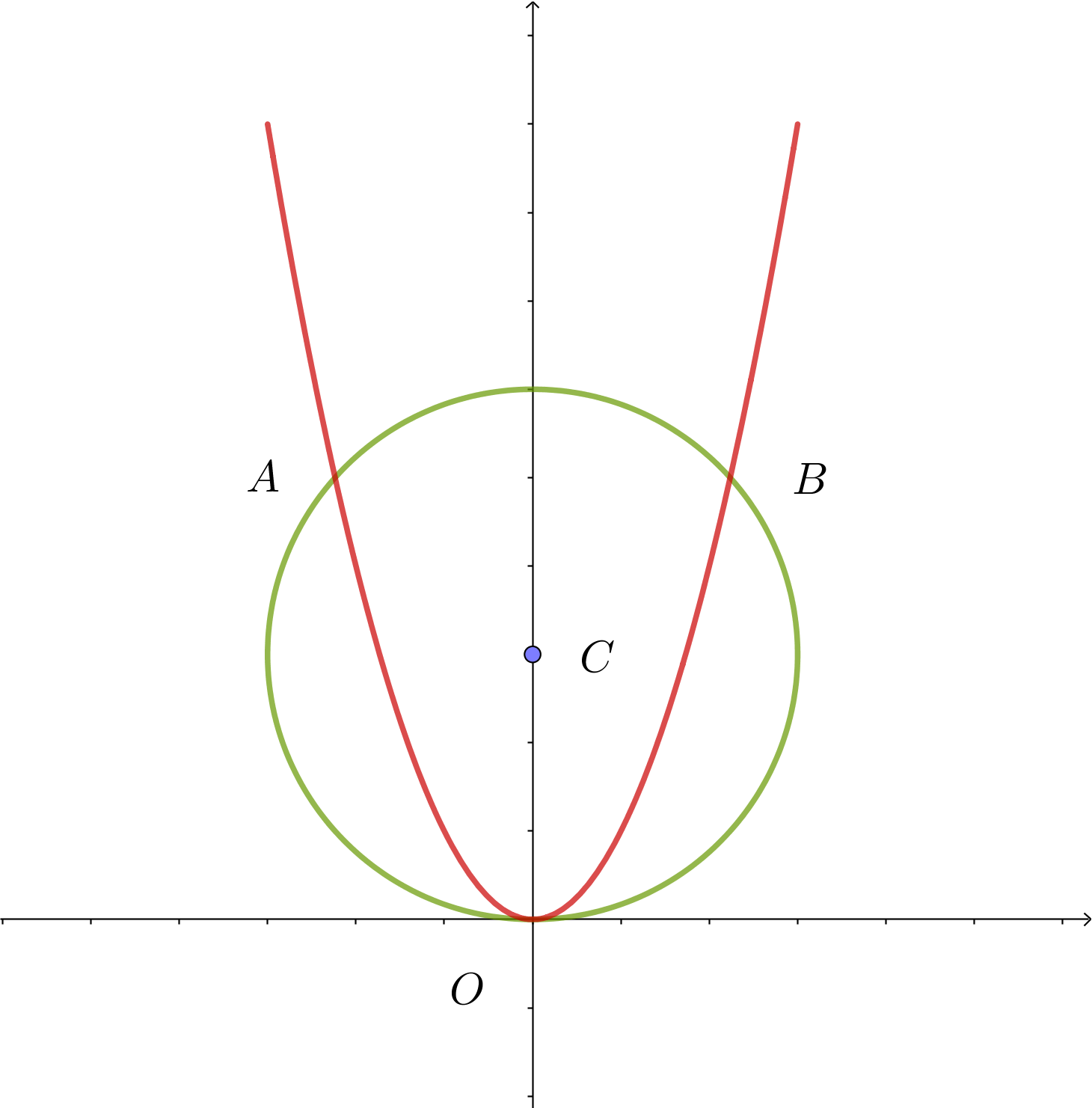
$p(t),\ q(t),\ r(t)\ を単に \ p,\ q,\ r\ と表す。$
$2\ 点 \ A,\ B\ は \ y\ 軸に関して対称だから、線分 \ AB\ の垂直二等分線上に$
$ある円の中心 \ C\ は\ y\ 軸上にある。$
$したがって \quad p(t)=0$
$AC=OC\ \ より \quad t^2+ (q-t^{2n})^2=q^2$
$\quad t^2-2qt^{2n}+t^{4n}=0 $
$\quad q=\cfrac{t^2+t^{4n}}{2t^{2n}}=\cfrac{1}{2}(t^{2-2n}+t^{2n})=\cfrac{1}{2}\big\{(t^2)^{1-n}+(t^2)^n\big\}$
$\quad n=2,\ 3,\ \cdots \ のとき \ \ 第 \ 1\ 項は \quad \cfrac{1}{t^2},\ \cfrac{1}{(t^2)^2},\ \cdots \quad となるから$
$\quad これらは \quad t \longrightarrow +0 \quad のとき \ \ +\infty \ \ に発散する。収束するのは \ \ n=1 \ のときである。$
$また、r=OC=q \quad だから \ \ q\ の条件が \ r\ の条件になる。$
$したがって、p,\ q,\ r\ がすべて収束するときは \quad n=1 \quad である。$
\[このとき、q=\cfrac{1}{2}(1+t^2) \quad だから \quad b=\lim _{t \rightarrow +0}q(t)=\cfrac{1}{2}\]
$\qquad p(t)=0 \quad より \quad a=0,\quad r(t)=q(t) \quad だから \quad c=\cfrac{1}{2}$
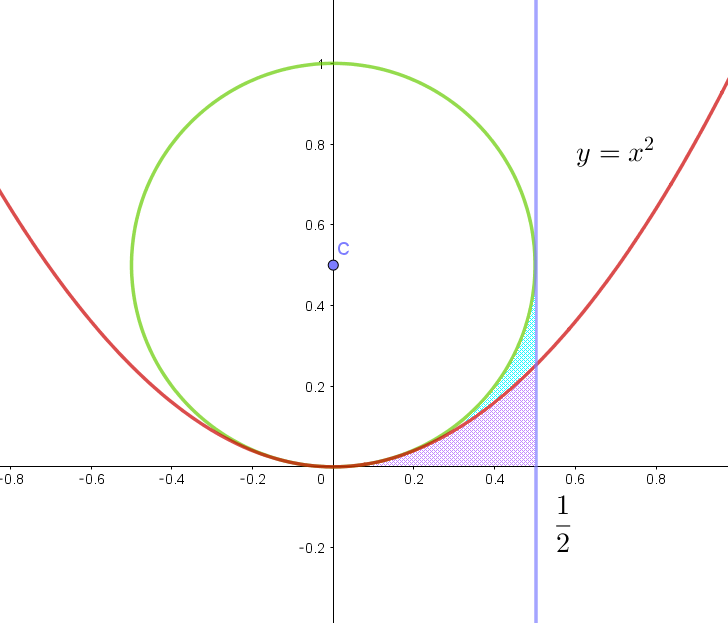
(2)
(i)$\ \ 0 \leqq x \leqq \cfrac{1}{2} \ \ の部分で、円 \ \ x^2+(y-\cfrac{1}{2})^2=\cfrac{1}{4}\ \ と \ x\ 軸で$
$\quad 挟まれた部分を回転して得られる体積 \ V_1\ は$
$\qquad (y-\cfrac{1}{2})^2=\cfrac{1}{4}-x^2 \ \ より$
$\quad 挟まれた部分は \quad y=\cfrac{1}{2}-\sqrt{\cfrac{1}{4}-x^2} \quad だから$
\begin{eqnarray*} V_1 &=&\pi \int _0^{\scriptsize{\cfrac{1}{2}}}\Big(\cfrac{1}{2}-\sqrt{\small{\cfrac{1}{4}}-x^2} \Big)^2dx\\ \\ &=&\pi \int _0^{\scriptsize{\cfrac{1}{2}}}\Big(\cfrac{1}{2}-x^2 - \sqrt{\small{\cfrac{1}{4}}-x^2} \Big)dx\\ \\ &=&\pi \big[\cfrac{1}{2}x -\cfrac{x^3}{3}\big]_0^{\scriptsize{\cfrac{1}{2}}} -\pi \int _0^{\scriptsize{\cfrac{1}{2}}} \sqrt{\small{\cfrac{1}{4}}-x^2} dx \hspace{3em} \big(第2項の積分は半径 \cfrac{1}{2}の円の面積の\cfrac{1}{4}\big)\\ \\ &=&\pi\big(\cfrac{1}{4}-\cfrac{1}{24}\big)-\pi \big(\pi \times \cfrac{1}{4} \times \cfrac{1}{4}\big)\\ \\ &=&\cfrac{5}{24}\pi-\cfrac{1}{16}\pi ^2 \end{eqnarray*} (ii)$\ \ 0 \leqq x \leqq \cfrac{1}{2}\ \ の部分で、放物線 \ \ y=x^2 \ \ と \ x\ 軸で挟まれた部分を回転して得られる体積 \ V_2\ は$
\[V_2=\pi \int _0^{\scriptsize{\cfrac{1}{2}}}x^4dx=\pi\big[\cfrac{x^5}{5}\big] _0^{\scriptsize{\cfrac{1}{2}}}=\cfrac{1}{160}\pi \]
$よって$
$\qquad V=V_1-V2=\big(\cfrac{5}{24}\pi-\cfrac{1}{16}\pi ^2\big) - \cfrac{1}{160}\pi=\cfrac{97}{480}\pi - \cfrac{1}{16}\pi ^2$
メインメニュー に戻る