岡山大学(理系) 2021年 問題2
$z\ は複素数で、z \ne 0,\ \ z \ne \pm 1 \ \ とする。このとき、以下の問いに答えよ。$
$(1)\ \ 複素数平面上の \ 3\ 点 \ A(1),\ B(z),\ C(z^2)\ が一直線上にあるための \ z\ についての必要十分条件を求めよ。$
$(2)\ \ 複素数平面上の \ 3\ 点 \ A(1),\ B(z),\ C(z^2)\ が \ \angle C\ を直角とする直角三角形の \ 3\ 頂点になるような \ z\ 全体の$
$\qquad 表す図形を複素数平面上に図示せよ。$
$(3)\ \ 複素数平面上の \ 3\ 点 \ A(1),\ B(z),\ C(z^2)\ が 直角三角形の \ 3\ 頂点になるような\ z\ 全体の表す図形を複素数$
$\qquad 平面上に図示せよ。$
$(解説)$
$(1)\ \ ベクトルをつかって、一直線上にある条件を表します。$
$(2)\ \ 三平方の定理を複素数で表現します。(1)の条件を忘れないこと。$
$(3)\ \ (2)と同様に残り \ 2\ パターンについて調べます。$
$なお、今年度の「東北大学(理系)の問題 \ 5」\ とほとんど一致してしています。全くの偶然でしょうが、$
$こんなこともあるのですね。$
(1)
$3\ 点 \ A,\ B,\ C\ が同一直線上にあるための条件は$
$\quad \vec{AC}=k\vec{AB}\ \ (kは実数)\ とおけるから \quad z^2 -1 =k(z-1) \qquad (z+1)(z-1)=k(z-1)$
$\quad z-1 \ne 0 \quad だから \quad z+1=k \qquad z=k-1$
$したがって \quad z\ は実数である。ただし、z \ne 0,\quad z \ne \pm 1$
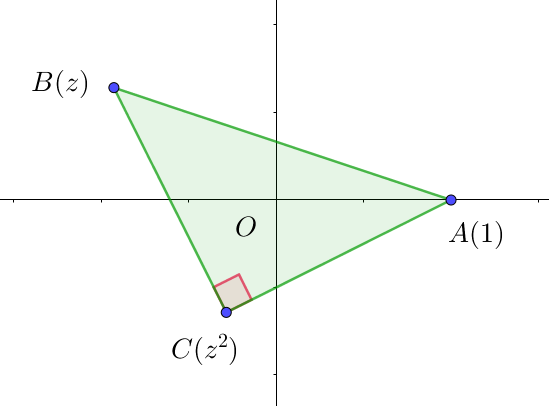
(2)
$\ \ \triangle ABC において$
$\quad AB^2=|z-1|^2$
$\quad BC^2=|z^2-z|^2=|z(z-1)|^2=|z|^2|z-1|^2$
$\quad AC=|z^2-1|=|(z+1)(z-1)|^2=|z+1|^2|z-1|^2$
$\quad \angle C=90° \quad より \quad AB^2=BC^2 + AC^2 \quad に代入して \quad |z-1|^2=|z|^2|z-1|^2+ |z+1|^2|z-1|^2$
$\quad |z-1| \ne 0 \quad だから 両辺を \ \ |z-1|^2 \ \ で割って \quad 1=|z|^2 + |z+1|^2 $
$\quad 1=z\overline{z}+(z+1)\overline{(z+1)} \qquad 1=z\overline{z}+(z+1)(\overline{z}+1)$
$\quad 2z\overline{z}+z+\overline{z}=0 \qquad z\overline{z}+\cfrac{1}{2}z+\cfrac{1}{2}\overline{z}=0$
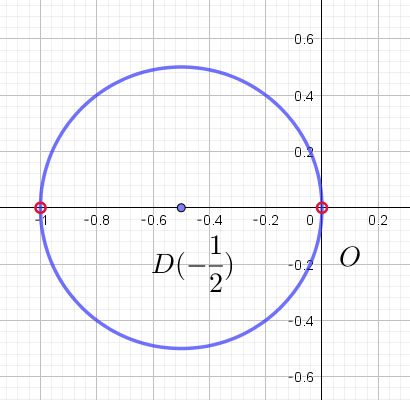
$\quad \big(z+\cfrac{1}{2}\big)\big(\overline{z}+\cfrac{1}{2}\big)=\cfrac{1}{4} \qquad |z+\cfrac{1}{2}|^2=\cfrac{1}{4} \qquad \therefore \ \ |z+\cfrac{1}{2}|=\cfrac{1}{2}$
$これは、D(-\cfrac{1}{2})\ \ を中心にもつ、半径 \ \ \cfrac{1}{2}\ \ の円を表す。$
$ただし、(1)より実軸上は、3\ 点 \ A,\ B,\ C\ が同一直線上にあるため除く$
(3)
(i)$\ \ \angle C=90°のときは(2)のとおり$
(ii)$\ \ \angle A=90°のとき$
$\quad BC^2=AB^2 + AC^2 \quad より \quad |z|^2|z-1|^2=|z-1|^2+ |z+1|^2|z-1|^2$
$\quad 両辺を \ \ |z-1|^2 \ \ で割って \quad |z|^2=1 + |z+1|^2 $
$\quad z\overline{z}=1+(z+1)\overline{(z+1)} \qquad z\overline{z}=1+(z+1)(\overline{z}+1)$
$\quad z+\overline{z}+2=0$
$\quad z=x+yi \quad とおくと \quad \overline{z}=x-yi \quad だから \quad (x+yi)+(x-yi)+2=0 \qquad \therefore \ \ x=-1$
(iii)$\ \ \angle B=90°\quad のとき$
$\quad AC^2=AB^2 + BC^2 \quad より \quad |z+1|^2|z-1|^2=|z-1|^2+ |z|^2|z-1|^2$
$\quad 両辺を \ \ |z-1|^2 \ \ で割って \quad |z+1|^2=1 + |z|^2 $
$\quad (z+1)\overline{(z+1)}=1+z\overline{z} \qquad (z+1)(\overline{z}+1)=1+z\overline{z}$
$\quad z+\overline{z}=0$
$\quad z=x+yi \quad とおくと \quad \overline{z}=x-yi \quad だから \quad (x+yi)+(x-yi)=0 \qquad \therefore \ \ x=0$
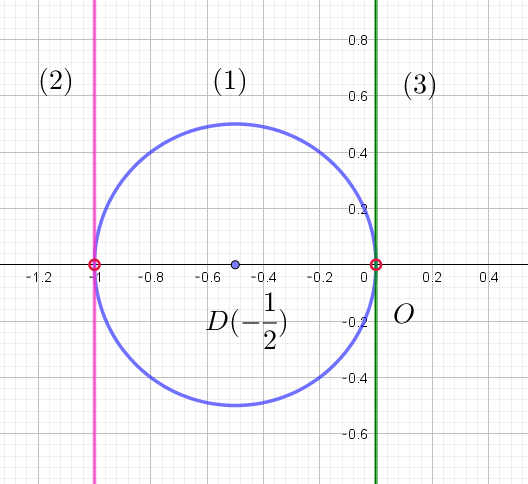
(i),(ii),(iii)$ \ の各場合の \ z\ を図示したものが右のグラフである。$
$ただし、(1)より \ z\ が実軸上にあるときは、3\ 点 \ O,\ A,\ B\ が同一直線上に$
$あるため、それらの点を除く。$
メインメニュー に戻る