お茶の水女子大学(数学専門) 2025年　問題1


$xy\ 平面において、実数 \ t\ に対し \ 2\ 点P(-4,\ 2t^2-4t-1),\ \ Q(4,\ 2t^2+4t-1)\ \ をとる。以下の問いに答えよ。$
$(1)\ \ 2\ 点P,\ Q\ を通る直線 \ \ell \ の方程式を求めよ。$
$(2)\ \ t\ が \ \ -1 \leqq t \leqq 1 \ \ の範囲を動くとき、線分PQ\ が通過する部分を \ D\ とする。ただし、その境界(境界線)$
$\quad も含むとする。$
(i)$\ \ 2\ 点A(1,\ -2),\ \ B(1,\ 3)\ \ は、それぞれ \ D\ に含まれないことを示せ。$
(ii)$\ \ D\ を図示し、その面積を求めよ。$


(1)


$\ell \ の傾き=\dfrac{(2t^2+4t-1)-(2t^2-4t-1)}{4-(-4)}=\dfrac{8t}{8}=t$

$\ell \ の方程式は \quad y=t(x+4)+2t^2-4t-1$

$\therefore \ \ y=tx+2t^2-1$


(2)


(i)$ $

$点A(0,\ -2)\ が線分PQ \ 上にあるとすると方程式 \ \ y=tx+2t^2-1\ \ をみたすから \quad -2=2t^2-1 $

$2t^2=-1 \quad となりこれをみたす実数 \ t\ は存在しない。$

$点B(1,\ 3) \ が線分PQ \ 上にあるとすると方程式 \ \ y=tx+2t^2-1 \ \ をみたすから \quad 3=t+2t^2-1$

$2t^2+t-4=0 \qquad t=\dfrac{-1 \pm\sqrt{33}}{4}$

$5 <\sqrt{33} <6 \quad だから \quad -6 <-\sqrt{33} < -5$

$\dfrac{-1-\sqrt{33}}{4} < -\dfrac{6}{4} <-1 ,\qquad \dfrac{-1+\sqrt{33}}{4} > \dfrac{4}{4}=1 $

$よって \quad t=\dfrac{-1 \pm\sqrt{33}}{4} \ \ は \quad -1 \leqq t \leqq 1 \ \ の範囲にない。$

$以上より\ \ 2\ 点A(1,\ -2),\ \ B(1,\ 3)\ \ は、それぞれ \ D\ に含まれない。$


(ii)$ $

$点P(-4,\ 2t^2-4t-1),\ \ Q(4,\ 2t^2+4t-1)\ \ に対して線分PQ \ が通過する部分とは、$

$-4 \leqq x \leqq 4 \quad で、y=tx+2t^2-1 \ \ (-1 \leqq t \leqq 1)\ \ をみたす実数 \ t\ が少なくとも \ 1\ つ$

$存在するような \ (x,\ y)\ のみたす条件である。$

$①\ \ 実数 \ t\ が2\ つ存在する場合$

$(ア) \ \ t\ は実数だから \ \ f(t)=0 \ \ の判別式 \ D\ について$

$\quad D=x^2-8(-y-1) \geqq 0$

$\quad y+1 \geqq -\dfrac{1}{8}x^2 $

$\quad y\geqq -\dfrac{1}{8}x^2-1$

$(イ) \ \ 端点について$

$f(-1)=2-x-y-1 \geqq 0 \qquad y \leqq -x+1 $

$f(1)=2+x-y-1 \geqq 0 \qquad y \leqq x+1 $

$なお$

$\quad y=-x+1 \ \ と \ \ y= -\dfrac{1}{8}x^2-1\ \ の交点は$

$\quad -\dfrac{1}{8}x^2-1=-x+1$

$\quad x^2-8x+16=0 \qquad (x-4)^2=0$

$\quad 重解 \ \ x=4\ をもつから点 C(4,\ -3)\ で接する。$

　

$\quad y=x+1 \ \ と \ \ y= -\dfrac{1}{8}x^2-1 \ \ の交点は$

$\quad -\dfrac{1}{8}x^2-1=x+1$

$\quad x^2+8x+16=0 \qquad (x+4)^2=0$

$\quad 重解 \ \ x=-4\ をもつから点 D(-4,\ -3)\ で接する。$

$(ウ) \ \ 軸について$

$\quad -1 \leqq -\dfrac{x}{4} \leqq 1 \qquad -4 \leqq x \leqq 4$

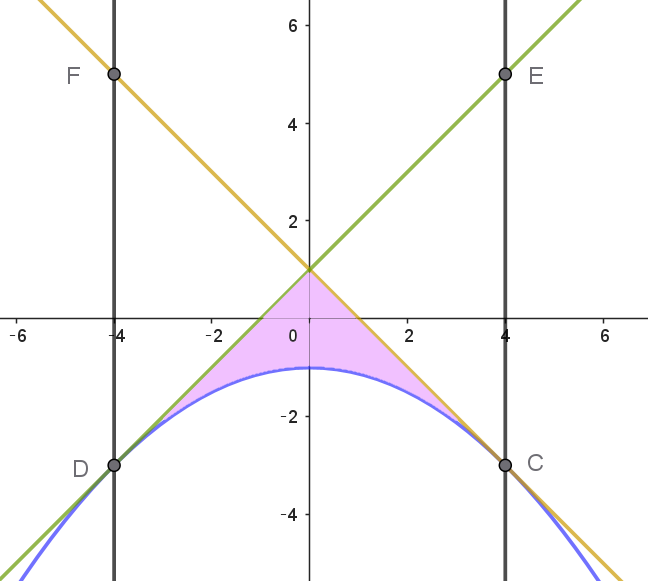
$①をみたす領域 は右図のとおり$

　

$②\ \ 実数 \ t\ が1\ つ存在する場合$

$f(-1)f(1) \leqq 0$

$(1-x-y)(1+x-y) \leqq 0$

$(y+x-1)(y-x-1) \leqq 0$

$②をみたす領域 は右図のとおり$


$よって、線分PQ\ が通過する部分は①または②\ をみたす領域Dで、$

$右図のとおり。なおグラフは \ y\ 軸について対称である。$

　

$D\ の面積 \ S\ は$
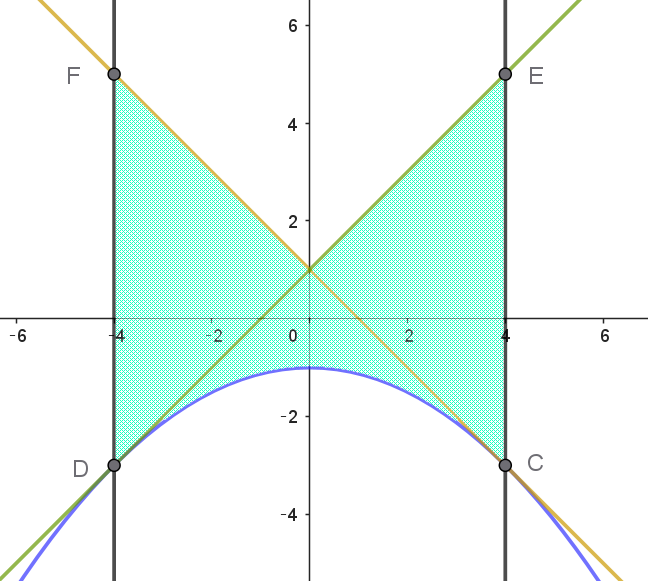
\begin{eqnarray*} S &=&2\int_0^4\{(x+1)-(-\dfrac{1}{8}x^2-1)\}dx\\ \\ &=&2\int_0^4 \big(\dfrac{1}{8}x^2+x+2\big)dx\\ \\ &=&2\big[\dfrac{x^3}{24}+\dfrac{x^2}{2}+2x\big]_0^4\\ \\ &=&2\big(\dfrac{16}{6}+8+8\big)\\ \\ &=&\dfrac{112}{3} \end{eqnarray*}

ページの先頭へ↑




メインメニュー　に戻る