お茶の水女子大学(数学A) 2023年 問題2
$下の図のように \ 1\ 辺の長さが \ 1\ の正八面体 \ ABCDEF\ とその \ 8\ つの面に接する球 \ S\ があり、$
$動点 \ P,\ Q\ は、それぞれ辺 \ AE,\ 辺 \ BC 上を \ AP=BQ\ \ を満たしながら動く。AP=BQ=t \ \ とし、$
$\vec{AB},\ \vec{AC},\ \vec{AD}\ \ をそれぞれ \ \ \vec{b},\ \vec{c},\ \vec{d}\ \ として、以下の問いに答えよ。$
$(1)\ \ 球Sの半径を求めよ。$
$(2)\ \ \vec{AP},\ \vec{AQ}\ を、それぞれ \ t,\ \vec{b},\ \vec{c},\ \vec{d}\ を用いて表せ。$
$(3)\ \ 線分 \ PQ\ が球 \ S\ と \ 1\ 点で接するときの \ t\ の値を求めよ。$
$\quad その接点を \ M\ とするとき、$
$\quad \vec{AM}\ を \ \vec{b},\ \vec{c},\ \vec{d}\ を用いて表せ。$
$(4)\ \ M\ は(3)で与えた点とし、R\ は辺 \ AB\ 上の動点とする。$
$\quad |\vec{MR}|+|\vec{RF}|\ \ が最小となるときの点 \ R\ に対する$
$\quad \vec{AR}\ を \ \vec{b}\ を用いて表せ。$
$\hspace{8em}$

(1)
$正方形 \ BCDE\ の対角線の交点を \ O\ とする。$
$面 \ ABC\ と球の接点を \ H\ 、AH\ の延長と辺 \ BC\ との交点を \ G\ とすると \quad OH \perp AG$
$正八面体と球の対称性から点 \ G\ は \ BC\ の中点である。$
$\triangle ABC\ は \ 1\ 辺 \ 1\ の正三角形 \ だから \quad AG \perp BC$
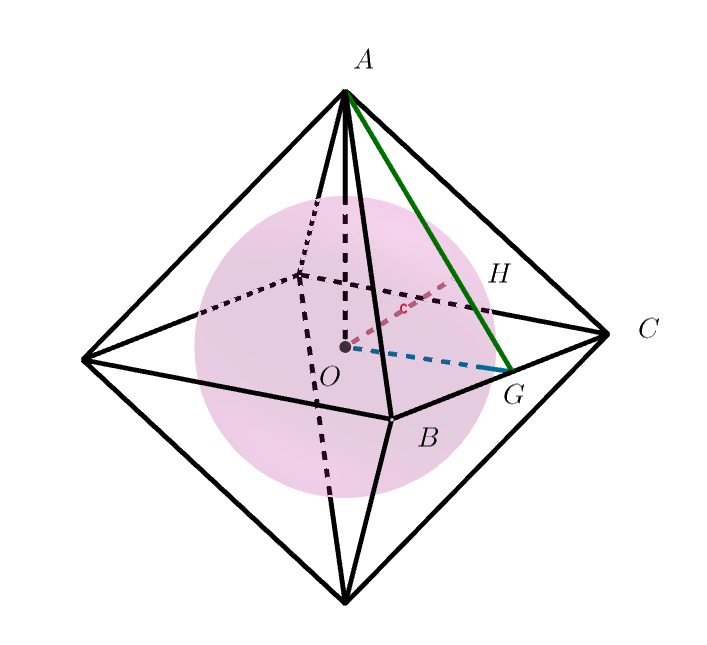
$\triangle OAG \ において $
$OG=\cfrac{1}{2}DC=\cfrac{1}{2},\quad OG \perp OA \quad だから$
$OA=\sqrt{AG^2-OG^2}=\sqrt{\cfrac{3}{4}-\cfrac{1}{4}}=\cfrac{\sqrt{2}}{2}$
$\triangle OAG=\cfrac{1}{2}OG\cdot OA=\cfrac{1}{2}AG\cdot OH \quad より$
$\cfrac{1}{2} \times \cfrac{\sqrt{2}}{2}=\cfrac{\sqrt{3}}{2} \times OH$
$OH=\cfrac{\sqrt{2}}{2\sqrt{3}}=\cfrac{\sqrt{6}}{6}$
$球Sの半径 \ r\ は \quad r=OH=\cfrac{\sqrt{6}}{6}$
(2)
\begin{eqnarray*} \vec{AE} &=&\vec{AB}+\vec{BE}\\ \\ &=&\vec{AB}+\vec{CD}\\ \\ &=&\vec{AB}+\vec{AD}-\vec{AC}\\ \\ &=&\vec{b}+\vec{d}-\vec{c}\\ \end{eqnarray*}
$よって \quad \vec{AP}=t\vec{AE}=t(\vec{b}-\vec{c}+\vec{d})$
$BC=1\ \ だから \ \ BQ:QC=t:1-t \qquad \therefore \ \ \vec{AQ}=(1-t)\vec{AB}+t\vec{AC}=(1-t)\vec{b}+t\vec{c}$
(3)
(i)$\ \ \vec{PM}=k\vec{PQ} \quad を満たす実数 \ k\ が存在する。$
$\quad \vec{PQ}=\vec{AQ}-\vec{AP}=(1-t)\vec{b}+t\vec{c} - t(\vec{b}-\vec{c}+\vec{d})=(1-2t)\vec{b}+2t\vec{c}-t\vec{d}$
$\quad \vec{AM}=p\vec{b}+q\vec{c}+r\vec{d}\ \ (p,\ q,\ r\ は実数)\ \ とおくと$
$\quad \vec{PM}=\vec{AM}-\vec{AP}=(p\vec{b}+q\vec{c}+r\vec{d})-t(\vec{b}-\vec{c}+\vec{d})=(p-t)\vec{b}+(q+t)\vec{c}+(r-t)\vec{d}$
$\quad (p-t)\vec{b}+(q+t)\vec{c}+(r-t)\vec{d}= k\{(1-2t)\vec{b}+2t\vec{c}-t\vec{d}\}$
\[ \hspace{1em} \left\{ \begin{array}{l} p-t=k(1-2t) \\ q+t=2kt \\ r-t=-kt \\ \end{array} \right. \]
$\quad \therefore \ \ p=(1-2k)t+k ,\quad q=(2k-1)t, \quad r=(1-k)t \hspace{5em}①$
(ii)$\ \ \vec{OM} \perp \vec{PQ} \quad より$
$\quad \vec{OM}=\vec{AM}-\vec{AO}=(p\vec{b}+q\vec{c}+r\vec{d})-\cfrac{1}{2}(\vec{b}+\vec{d})=(p-\cfrac{1}{2})\vec{b}+q\vec{c}+(r-\cfrac{1}{2})\vec{d}$
$\quad \{(p-\cfrac{1}{2})\vec{b}+q\vec{c}+(r-\cfrac{1}{2})\vec{d}\} \cdot \{(1-2t)\vec{b}+2t\vec{c}-t\vec{d}\}=0$
$\quad (p-\cfrac{1}{2})(1-2t)|\vec{b}|^2+(p-\cfrac{1}{2})(2t)\vec{b}\cdot \vec{c}+(p-\cfrac{1}{2})(-t)\vec{b}\cdot \vec{d}+q(1-2t)\vec{c} \cdot \vec{b} +2qt|\vec{c}|2-qt\vec{c}\cdot \vec{d}+$
$ \hspace{3em} +(r-\cfrac{1}{2})(1-2t)\vec{d} \cdot \vec{b}+(r-\cfrac{1}{2})(2t)\vec{d} \cdot \vec{c}-(r-\cfrac{1}{2})t|\vec{d}|^2\}=0$
$\quad ここで$
$\quad 正八面体 \ ABCDEF\ の\ 1\ 辺の長さは \ 1\ だから \quad |\vec{b}|= |\vec{c}|= |\vec{d}|=1$
$\quad 各面は正三角形だから \quad \vec{b}\cdot \vec{c}=|\vec{b}||\vec{c}|\cos 60°=\cfrac{1}{2}, \qquad \vec{c}\cdot \vec{d}=|\vec{c}||\vec{d}|\cos 60°=\cfrac{1}{2}$
$\quad 四角形BCDE\ は \ 1\ 辺 \ 1\ の正方形だから \quad BD=\sqrt{2}$
$\quad \triangle ABD \ において \quad AB=AD=1, \quad BD=\sqrt{2} \quad だから \quad BD^2=AB^2+AD^2 \quad となり$
$\quad \angle BAD=90°\quad したがって \quad \vec{b}\cdot \vec{d}=0$
$これらを使ってまとめると$
$\quad (p-\cfrac{1}{2})(1-2t)+(p-\cfrac{1}{2})t +\cfrac{1}{2}q(1-2t)+2qt-\cfrac{1}{2}qt+(r-\cfrac{1}{2})t-(r-\cfrac{1}{2})t=0$
$\quad p(1-t)+\cfrac{1}{2}t+\cfrac{1}{2}q(1+t)-\cfrac{1}{2}=0 $
$\quad ①を代入して$
$\quad \{(1-2k)t+k\}(1-t)+\cfrac{1}{2}t+\cfrac{1}{2}(2k-1)t(1+t)-\cfrac{1}{2}=0 $
$\quad (3k-\cfrac{3}{2})t^2+(1-2k)t+k-\cfrac{1}{2}=0$
$\quad 3(k-\cfrac{1}{2})t^2-2(k-\cfrac{1}{2})t+k-\cfrac{1}{2}=0$
$\quad (k-\cfrac{1}{2})(3t^2-2t+1)=0 \quad ここで \quad 3t^2-2t+1=3(t-\cfrac{1}{3})^2+\cfrac{2}{3} > 0 \quad だから$
$\quad k=\cfrac{1}{2}$
$\quad ①より \quad p=\cfrac{1}{2},\quad q=0,\quad r=\cfrac{1}{2}t$
$\quad このとき$
$\quad \vec{OM}=(p-\cfrac{1}{2})\vec{b}+q\vec{c}+(r-\cfrac{1}{2})\vec{d}=\cfrac{1}{2}(1-t)\vec{d}$
$\quad OM=r \quad より \quad |\vec{OM}|=\cfrac{\sqrt{6}}{6} \quad だから$
$\quad \cfrac{1}{2}(1-t)|\vec{d}|=\cfrac{\sqrt{6}}{6}$
$\quad \cfrac{1}{2}(1-t)=\cfrac{\sqrt{6}}{6}$
$\quad \therefore \ \ t=\cfrac{3-\sqrt{6}}{3}$
$\quad よって$
$\quad \vec{AM}=p\vec{b}+q\vec{c}+r\vec{d}=\cfrac{1}{2}\vec{b}+\cfrac{1}{2}t\vec{d}=\cfrac{1}{2}\vec{b}+\cfrac{1}{2}\times \cfrac{3-\sqrt{6}}{3}\vec{d}=\cfrac{1}{2}\vec{b}+\cfrac{3-\sqrt{6}}{6}\vec{d}$
(4)
$(3)より \quad \vec{AM}=\cfrac{1}{2}\vec{b}+\cfrac{3-\sqrt{6}}{6}\vec{d} \quad と表されるから$
$点 \ M\ は \ \vec{b}\ と \ \vec{d}\ のつくる平面、すなわち正方形 \ ABFD\ 上にある。$
$さらに、\cfrac{3-\sqrt{6}}{6} < 1 \ \ だから点 \ M\ は正方形 \ ABFD\ の内部にある。$

$\vec{b}\ 成分は同じで、\vec{d}\ 成分は逆向きだから \quad \vec{AN}=\cfrac{1}{2}\vec{b}-\cfrac{3-\sqrt{6}}{6}\vec{d}$
$|\vec{MR}|+|\vec{RF}|=|\vec{NR}|+|\vec{RF}|\ \ が最小となるのは、$
$3\ 点\ N,\ R,\ F\ が一直線上にあるときである。$
$よって、\vec{AR}=u\vec{AN}+(1-u)\vec{AF}\ \ を満たす実数 \ u\ が存在する。$
$一方、点 \ R\ は辺 \ AB\ 上の点だから \ \ \vec{AR}=v\vec{AB}\ \ を満たす実数 \ v\ が存在するから$
$v\vec{AB}=u\vec{AN}+(1-u)\vec{AF}$
$v\vec{b}=u\big(\cfrac{1}{2}\vec{b}-\cfrac{3-\sqrt{6}}{6}\vec{d}\big) + (1-u)(\vec{b}+\vec{d})$
$v\vec{b}=(1-\cfrac{u}{2})\vec{b}+\big(1-\cfrac{9-\sqrt{6}}{6}u\big)\vec{d}$
\[ \hspace{1em} \left\{ \begin{array}{l} v=1-\cfrac{u}{2} \hspace{8em}①\\ 1-\cfrac{9-\sqrt{6}}{6}u=0 \hspace{5em}②\\ \end{array} \right. \] $②より \quad u=\cfrac{6}{9-\sqrt{6}}=\cfrac{2(9+\sqrt{6})}{25}$
$①に代入して \quad v=1-\cfrac{9+\sqrt{6}}{25}=\cfrac{16-\sqrt{6}}{25}$
$よって \ \ |\vec{MR}|+|\vec{RF}|\ \ が最小となるのは \quad \vec{AR}=\cfrac{16-\sqrt{6}}{25}\vec{b} \quad のときである。$
メインメニュー に戻る