お茶の水女子大学(理学共通) 2025年　問題2


$平面において \ OA=3,\ \ OB=2,\ \ AB=\sqrt{7}\ \ である三角形OAB\ を考える。直線AB\ 上の点P\ を、線分OP\ と$
$直線AB\ が垂直となるようにとる。\vec{a}=\vec{OA},\ \ \vec{b}=\vec{OB}\ \ として以下の問いに答えよ。$
$(1)\ \ 内積\ \ \vec{a}\cdot \vec{b} \ \ の値を求めよ。$
$(2)\ \ ベクトル \ \vec{OP}\ を \ \vec{a},\ \ \vec{b}\ \ を用いて表せ。$
$(3)\ \ 線分AB\ 上に \ \angle POQ =\dfrac{\pi}{6} \ \ となる点Q\ がただ一つあることを示し、ベクトル \ \vec{OQ}\ を\ \vec{a},\ \ \vec{b} \ \ を用いて表せ。$


(1)

　

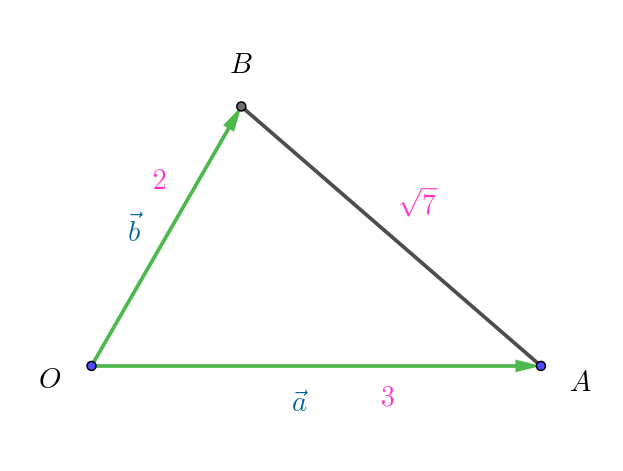
$OA=|\vec{a}|=3,\quad OB=|\vec{b}|=2,\quad AB=|\vec{AB}|=\sqrt{7} \quad より$

$|\vec{b}-\vec{a}|^2=7$

$|\vec{b}|^2+|\vec{a}|^2-2\vec{a}\cdot \vec{b}=7$

$4+9-2\vec{a}\cdot \vec{b}=7$

$\therefore \ \ \vec{a}\cdot \vec{b}=3$


(2)

　

$AP:PB=k:(1-k)\ \ とおくと$

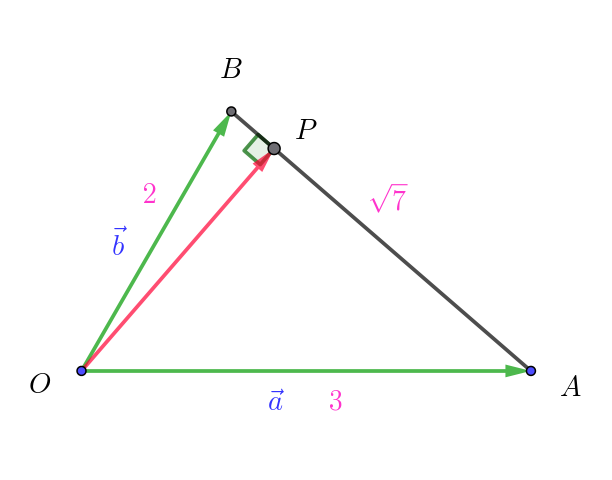
$\vec{OP}=(1-k)\vec{OA}+k\vec{OB}=(1-k)\vec{a}+k\vec{b}$

$OP \perp AB \quad より \quad \vec{OP} \cdot \vec{AB}=0$

$\{(1-k)\vec{a} + k\vec{b}\} \cdot (\vec{b} -\vec{a})=0$

$\{(1-2k)\vec{a}\cdot \vec{b}-(1-k)|\vec{a}|^2 +k|\vec{b}|^2=0$

$(1-2k) \times 3 -(1-k) \times 9 +k \times 4=0$

$7k-6=0 \qquad \therefore \ \ k=\dfrac{6}{7}$

$よって \quad \vec{OP}=\dfrac{1}{7}\vec{a}+\dfrac{6}{7}\vec{b}$


(3)

　

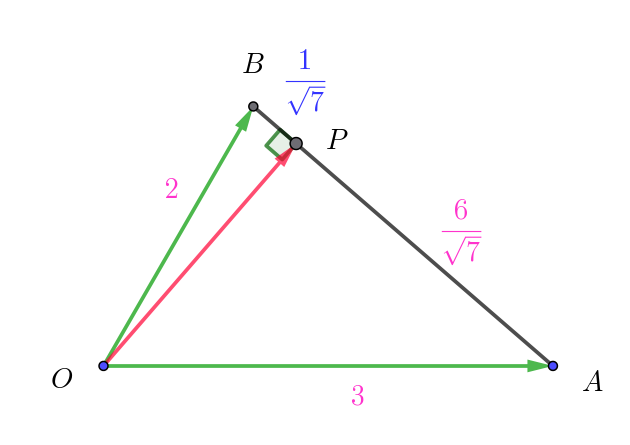
$(2)より \quad AP=\sqrt{7} \times \dfrac{6}{7}=\dfrac{6}{\sqrt{7}},\quad PB=\sqrt{7} \times \dfrac{1}{7}=\dfrac{1}{\sqrt{7}}$

(i)$\ \ 直角三角形OBP\ において$

$\quad OP=\sqrt{4-\dfrac{1}{7}}=\dfrac{3\sqrt{3}}{\sqrt{7}}$

$\quad \sin \angle BOP=\dfrac{BP}{OB}=\dfrac{\dfrac{1}{\sqrt{7}}}{2}=\dfrac{1}{2\sqrt{7} \quad }<\dfrac{1}{2}=\sin \dfrac{\pi}{6}$

$\quad \sin \theta \ \ は \quad 0 < \theta < \dfrac{\pi}{2} \quad で単調増加だから \quad \angle BOP < \dfrac{\pi}{6}$

$\quad したがって　線分BP\ 上に \ \angle POQ =\dfrac{\pi}{6} \ \ となる点Q\ はとれない$

(ii)$\ \ 直角三角形OAP \ において$

　

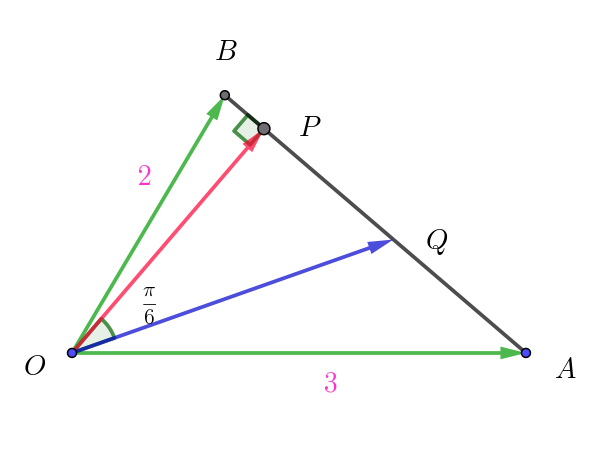
$\quad \sin \angle AOP=\dfrac{AP}{OA}=\dfrac{\dfrac{6}{\sqrt{7}}}{3}=\dfrac{2}{\sqrt{7}}$

$\quad \big(\dfrac{2}{\sqrt{7}}\big)^2=\dfrac{4}{7}=\dfrac{16}{28},\qquad \big(\dfrac{1}{2}\big)^2=\dfrac{1}{4}=\dfrac{7}{28}$

$よって \quad \sin \angle AOP=\dfrac{2}{\sqrt{7}} > \dfrac{1}{2}=\sin \dfrac{\pi}{6}$

$\quad \angle AOP > \dfrac{\pi}{6} \quad だから線分AP\ 上に \ \angle POQ =\dfrac{\pi}{6} \ \ となる点Q\ がとれる。$

(i),(ii)$\ \ より\ \ 線分AB\ 上に \ \angle POQ =\dfrac{\pi}{6} \ \ となる点Q\ がただ一つある。$

$直角三角形OPQにおいて$

$\quad PQ=OP\tan \dfrac{\pi}{6}=\dfrac{3\sqrt{3}}{\sqrt{7}} \times \dfrac{1}{\sqrt{3}}=\dfrac{3}{\sqrt{7}}$

$\quad AQ=AP-PQ=\dfrac{6}{\sqrt{7}}- \dfrac{3}{\sqrt{7}}=\dfrac{3}{\sqrt{7}}$

$よって、点Q\ は線分AP\ の中点だから$

$\vec{OQ}=\dfrac{1}{2}(\vec{OA}+\vec{OP})=\dfrac{1}{2}\big(\vec{a}+\big(\dfrac{1}{7}\vec{a}+\dfrac{6}{7}\vec{b}\big)\big)=\dfrac{4}{7}\vec{a}+\dfrac{3}{7}\vec{b}$


ページの先頭へ↑




メインメニュー　に戻る