お茶の水女子大学 2021年 B問題2
$共通の接線 \ l\ をもつ円 \ C_1,\ C_2,\ C_3\ の半径をそれぞれ \ r_1,\ r_2,\ r_3\ とする。これらの円のどの二つも互いに$
$外接しており、C_3\ は \ l,\ C_1,\ C_2\ に囲まれた領域に含まれているものとする。以下の問いに答えよ。$
$(1)\ \ \cfrac{1}{\sqrt{r_3}}=\cfrac{1}{\sqrt{r_1}}+\cfrac{1}{\sqrt{r_2}}\ \ となることを示せ。$
$(2)\ \ r_3=1 \ のとき、r_1 + r_2\ \ の取り得る値の最小値を求めよ。$
$(解説)$
$(1)\ \ 2\ 円の外接条件は、中心間距離=半径の和 \ \ です。$
$(2)\ \ 図形の問題から離れて、条件付きの不等式の証明問題ととらえます。いくつかの方法が考えられます。$
(1)
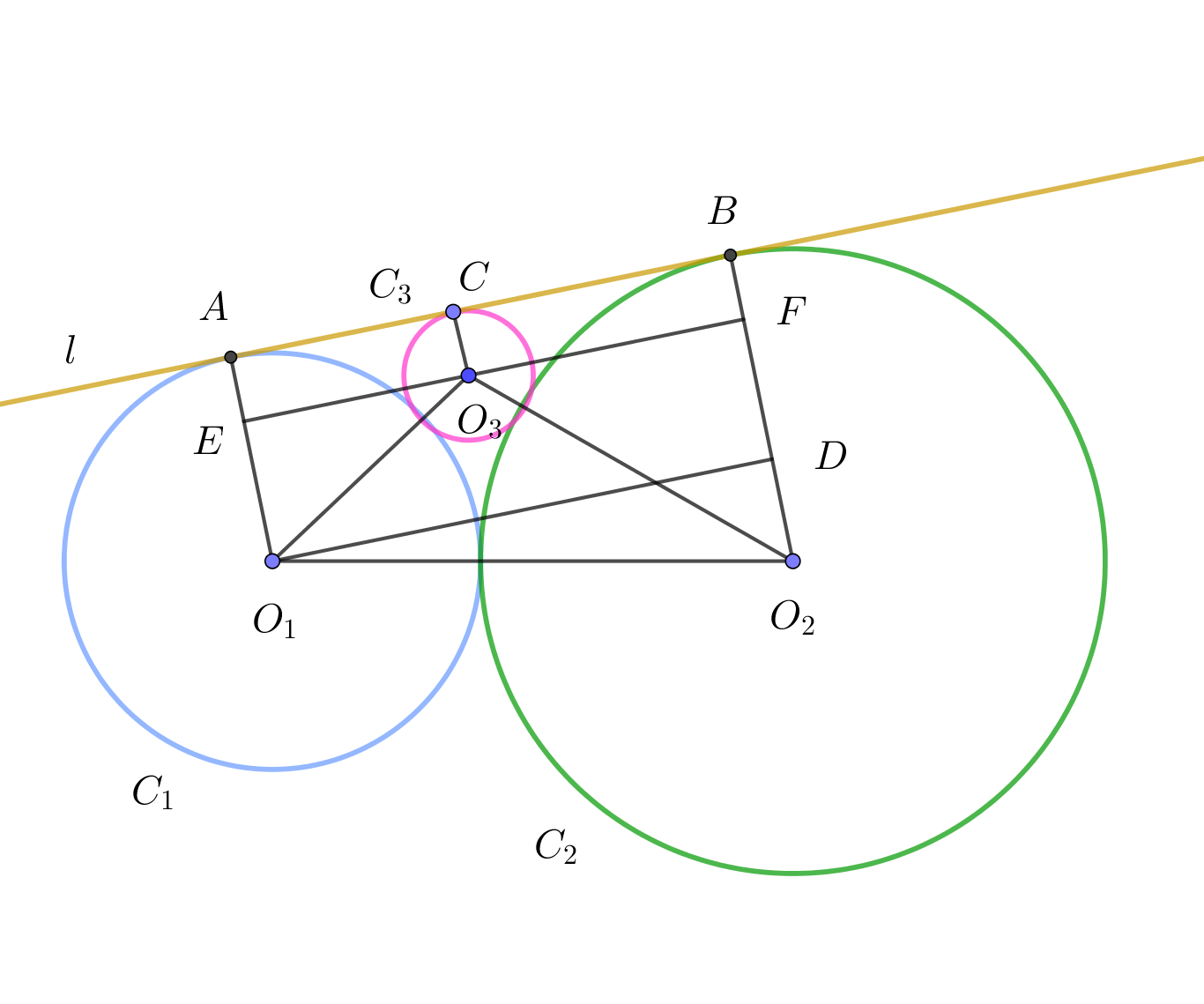
$r_1 < r_2 \ \ の場合を考える。題意を満たす図は右のとおりである。$
$\quad r_1 > r_2 \ \ の場合はこの図をひっくり返せばよい。$
$C_1,\ C_2,\ C_3\ と \ l\ との接点を \ A,\ B,\ C\ とすると$
$\quad O_1A \perp l,\quad O_2B \perp l ,\quad O_3C \perp l$
$O_1D \perp O_2B,\quad O_1D /\!/ EO_3 \quad とし、EO_3\ を延長し、O_2B \ との交点を$
$F\ とすると、四角形 \ O_1DBA と\ O_1DFE\ は長方形となる。$
$2\ 円が外接するときは、中心間距離=半径の和 \ \ である。$
(i)
$\quad O_2D=O_2B-DB=O_2B-O_1A=r_2-r_1 \quad だから$
$\quad EF=O_1D=\sqrt{O_1 O_2^2-O_2D^2}=\sqrt{(r_1+r_2)^2-(r_2-r_1)^2}=2\sqrt{r_1r_2}$
(ii)
$\quad O_1E=O_1A-EA=O_1A-O_3C=r_1-r_3,\qquad O_2F=O_2B-FB=O_2F-O_3C=r_2-r_3$
$\qquad EO_3=\sqrt{O_1 O_3^2-O_1E ^2}=\sqrt{(r_1+r_3)^2-(r_1-r_3)^2}=2\sqrt{r_1r_3}$
$\qquad FO_3=\sqrt{O_2O_3^2-O_2F^2}=\sqrt{(r_2+r_3)^2-(r_2-r_3)^2}=2\sqrt{r_2r_3}$
$\quad EF=EO_3+FO_3=2\sqrt{r_1r_3}+2\sqrt{r_2r_3}$
(i),(ii)$\ \ より$
$\quad EF=2\sqrt{r_1r_2}=2\sqrt{r_1r_3}+2\sqrt{r_2r_3}$
$\quad 両辺を \ \ 2\sqrt{r_1r_2r_3}\ \ で割って$
$\quad \cfrac{1}{\sqrt{r_3}}=\cfrac{1}{\sqrt{r_1}}+\cfrac{1}{\sqrt{r_2}} $
(2)
$\quad \cfrac{1}{\sqrt{r_1}}=s,\quad \cfrac{1}{\sqrt{r_2}}=t\quad とおくと \quad r_3=1 \quad より \quad s+t=1$
$\quad 相加・相乗平均の不等式より \quad s+t \geqq 2\sqrt{st} \quad だから \quad st \leqq \cfrac{(s+t)^2}{4}=\cfrac{1}{4}$
$\qquad ただし等号は \quad s=t=\cfrac{1}{2} \quad すなわち \quad r_1=r_2=4\ \ のとき$
$\qquad r_1+r_2=\cfrac{1}{s^2}+\cfrac{1}{t^2}=\cfrac{(s+t)^2-2st}{s^2t^2}=\cfrac{1-2st}{s^2t^2}$
$\quad ここから先は \ 3\ 通りの方法が考えられます。$
$解1$
$\quad -2st \geqq -\cfrac{1}{2}\quad より \quad 1-2st \geqq \cfrac{1}{2}$
$\quad 0 < s^2 t^2 \leqq \cfrac{1}{16} \quad より \quad \cfrac{1}{s^2t^2} \geqq 16$
$\quad 辺々かけて \qquad \cfrac{1-2st}{s^2t^2} \geqq \cfrac{1}{2} \times 16=8$
$\quad よって \quad r_1+r_2 \quad の最小値は \quad 8$
$解2$
$\quad st=u ,\quad R=r_1+r_2=\cfrac{1-2u}{u^2} \quad とおくと$
$\quad Ru^2+2u-1=0 \quad を解いて \quad u > 0 \quad だから \quad u=\cfrac{-1+\sqrt{1+R}}{R}$
$\quad \cfrac{-1+\sqrt{1+R}}{R} \leqq \cfrac{1}{4} \quad より \quad \sqrt{1+R} \leqq \cfrac{R}{4}+1 \qquad 1+R \leqq \big(\cfrac{R}{4}+1\big)^2$
$\quad \cfrac{R^2}{16}-\cfrac{R}{2} \geqq 0 \qquad R^2-8R \geqq 0$
$\quad R(R-8) \geqq 0 \qquad R > 0 \quad だから \quad R \geqq 8$
$解3$
$\quad st=u ,\quad R=\cfrac{1-2u}{u^2} \quad とおくと$
$\quad f(u)=Ru^2+2u-1=0 \ \ の判別式は \quad \cfrac{D}{4}=1+R > 0 \quad だから$
$\quad f(u)=0 \ \ は異なる2つの実数解\ \ u_1,\ \ u_2\ \ をもつ。$
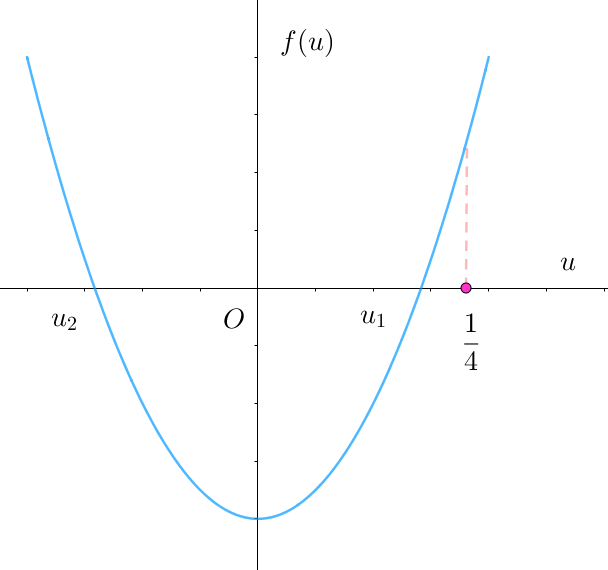
$\quad u_1u_2=-\cfrac{1}{R} < 0 \quad だから \quad u_1,\ u_2 \ \ は異符号 \qquad u_2 < 0 ,\ \ u_1 > 0 \ \ とすると$
$\quad u \leqq \cfrac{1}{4} \quad だから \quad f(\cfrac{1}{4}) \geqq 0$
$\quad \cfrac{R}{16} + \cfrac{1}{2}-1 \geqq 0 \qquad \cfrac{R}{16} \geqq \cfrac{1}{2} \qquad \therefore \ \ R \geqq 8 $
メインメニュー に戻る