お茶の水女子大学 2021年 A問題2
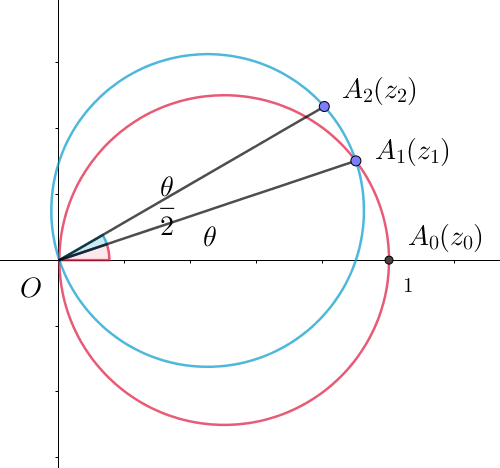
$0 < \theta < \cfrac{\pi}{2} , \ z_0=1\ とする。複素数平面の原点を \ O,\ z_0\ のあらわす点を \ A_0\ とする。線分 \ OA_0\ を直径と$
$する円上の点 \ A_1(z_1)\ で \ z_1 \ne 0 ,\ \ \angle A_0OA_1=\theta \ であり \ \ \cfrac{z_1}{z_0}\ \ の虚部が正であるものを考える。$
$同様に \ n=1,\ 2,\ \cdots \ に対して、線分 \ OA_n\ を直径とする円上の点 \ A_{n+1}(z_{n+1})\ で \ z_{n+1} \ne 0 ,$
$\angle A_nOA_{n+1}=\cfrac{\theta}{2^n} \ であり \ \cfrac{z_{n+1}}{z_n}\ の虚部が正であるものを考える。このとき、以下の問いに答えよ。$
$(1)\ \ すべての自然数 \ n\ について次が成り立つことを示せ。$
$\hspace{3em} |z_n|=\cfrac{\sin 2\theta}{2^n\sin \big(\dfrac{\theta}{2^{n-1}}\big)}$
$(2)\ \ 0 < x < \theta \ \ のとき、\cfrac{\sin \theta}{\theta} < \cfrac{\sin x}{x} < 1 \ \ が成り立つことを示せ。$
$(3)\ \ 三角形 \ A_nOA_{n+1}\ の面積を \ S_n \ とするとき、次が成り立つことを示せ。$
\[\hspace{3em} \cfrac{\sin ^2 2\theta}{8\theta} < \sum _{n=1}^{\infty} S_n < \cfrac{\sin ^2 2\theta}{8\sin \theta}\]
$(解説)$
$(1)\ \ |z_n|\ の漸化式を導き、\sin \theta \ \ の半角の公式をつかいます。$
$(2)\ \ 微分法を用いて、左右の不等号を別々に証明します。$
$(3)\ \ S_n \ は簡単に求まりますので、(1)と(2)をつかって示します。$
(1)
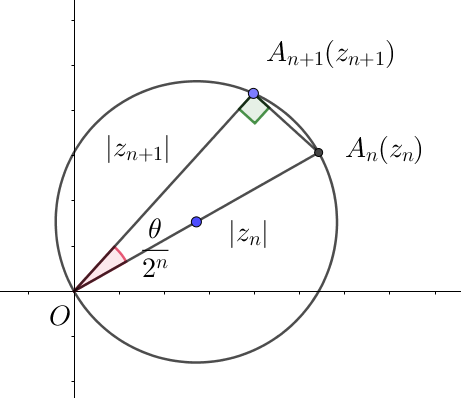
$点 \ A_{n+1}\ は \ OA_n\ を直径とする円周上にあるから、円周角の定理により$
$\angle OA_{n+1}A_n =90°\quad だから \quad \cfrac{|z_{n+1}|}{|z_n|}=\cos \cfrac{\theta}{2^n}$
$\cfrac{|z_n|}{|z_{n-1}|} \times \cfrac{|z_{n-1}|}{|z_{n-2}|} \times \cdots \times \cfrac{|z_1|}{|z_0|}=\cos \cfrac{\theta}{2^{n-1}} \cos \cfrac{\theta}{2^{n-2}} \cdots \cos \cfrac{\theta}{2^0}$
$\cfrac{|z_n|}{|z_0|}= \cos \cfrac{\theta}{2^{n-1}} \cos \cfrac{\theta}{2^{n-2}} \cdots \cos \cfrac{\theta}{2^0}$
$|z_0|=1 \quad だから \quad |z_n|= \cos \cfrac{\theta}{2^{n-1}} \cos \cfrac{\theta}{2^{n-2}} \cdots \cos \cfrac{\theta}{2} \cos \theta \hspace{5em}①$
$一方$
\begin{eqnarray*}
\sin \theta
&=&2\sin \cfrac{\theta}{2}\cos \cfrac{\theta}{2}\\
\\
&=&2^2\sin \cfrac{\theta}{2^2}\cos \cfrac{\theta}{2^2}\cos \cfrac{\theta}{2}\\
\end{eqnarray*}
$\hspace{5em} \vdots $
$\hspace{4em}\ =2^{n-1}\sin \cfrac{\theta}{2^{n-1}}\cos \cfrac{\theta}{2^{n-1}} \cdots \cos \cfrac{\theta}{2}$
$よって \qquad \cos \cfrac{\theta}{2} \cos \cfrac{\theta}{2^2} \cdots \cos \cfrac{\theta}{2^{n-1}}=
\cfrac{\sin \theta}{2^{n-1}\sin \cfrac{\theta}{2^{n-1}}}$
$①に代入して$
$\qquad |z_n|=\cfrac{\sin \theta \cos \theta}{2^{n-1}\sin \cfrac{\theta}{2^{n-1}}}=\cfrac{\sin 2\theta}{2^n\sin \dfrac{\theta}{2^{n-1}}}$
(2)
(i)$\ \ \cfrac{\sin \theta}{\theta} < \cfrac{\sin x}{x} \quad の証明$
$\quad f(x)=\cfrac{\sin x}{x} \quad とおくと \quad f'(x)=\cfrac{x\cos x - \sin x}{x^2}$
$\quad g(x)=x\cos x - \sin x \quad とおくと \quad g'(x)=\cos x -x\sin x -\cos x=-x\sin x$
$\quad 0 < x < \cfrac{\pi}{2} \quad だから \quad g'(x) < 0 $
$\quad g(x) は単調減少だから \quad g(x) < g(0)=0$
$\quad よって \quad f'(x) < 0 \quad となり、f(x)\ は単調減少$
$\quad \theta > x \quad だから \quad f(\theta) < f(x) \quad より \quad \cfrac{\sin \theta }{\theta} < \cfrac{\sin x}{x}$
(ii)$\ \ \cfrac{\sin x}{x} < 1 \quad の証明$
$\quad h(x)=x-\sin x \quad とおくと \qquad h'(x)=1-\cos x > 0$
$\quad h(x) は単調増加だから \quad h(x) > h(0)=0$
$\quad \sin x < x \quad より \quad \cfrac{\sin x}{x} < 1 $
(i),(ii)$\ より \quad \cfrac{\sin \theta}{\theta} < \cfrac{\sin x}{x} < 1 $
(3)
\begin{eqnarray*} S_n &=&\cfrac{1}{2}OA_{n+1}\cdot A_nA_{n+1}\\ \\ &=&\cfrac{1}{2}|z_n|^2 \cos \cfrac{\theta}{2^n} \sin \cfrac{\theta}{2^n}\\ \\ &=&\cfrac{|z_n|^2}{2^2} \sin \cfrac{\theta}{2^{n-1}}\\ \\ &=&\cfrac{\sin ^2 2\theta}{2^{2n+2}\sin ^2 \dfrac{\theta}{2^{n-1}}} \times \sin \cfrac{\theta}{2^{n-1}}\\ \\ &=&\cfrac{\sin ^2 2\theta}{2^{2n+2}\sin \dfrac{\theta}{2^{n-1}}}\\ \end{eqnarray*} (i)$\ \ 左の不等号の証明$
$\quad 0 < x < \cfrac{\pi}{2} \quad のとき \quad 0 < \cfrac{\sin x}{x} < 1 \quad より \quad \cfrac{x}{\sin x} > 1$
$\quad x=\cfrac{\theta}{2^{n-1}} \quad とおくと \quad 0 < \cfrac{\theta}{2^{n-1}} < \cfrac{\pi}{2} \quad だから \quad \cfrac{\dfrac{\theta}{2^{n-1}}}{\sin \dfrac{\theta}{2^{n-1}}} > 1$
\begin{eqnarray*} S_n &=&\cfrac{\sin ^2 2\theta}{2^{2n+2}}\cdot \cfrac{2^{n-1}}{\theta} \cdot \cfrac{\dfrac{\theta}{2^{n-1}}}{\sin \dfrac{\theta}{2^{n-1}}}\\ \\ &>&\cfrac{\sin ^2 2\theta}{2^{2n+2}}\cdot \cfrac{2^{n-1}}{\theta}\\ \\ &=&\cfrac{\sin ^2 2\theta}{\theta} \cdot \cfrac{1}{2^{n+3}}\\ \end{eqnarray*}
\begin{eqnarray*} \sum _{n=1}^\infty S_n &>&\sum _{n=1}^\infty \cfrac{\sin ^2 2\theta}{\theta} \cdot \cfrac{1}{2^{n+3}}\\ \\ &=& \cfrac{\sin ^2 2\theta}{\theta} \sum _{n=1}^\infty \cfrac{1}{2^{n+3}}\\ \\ &=& \cfrac{\sin ^2 2\theta}{\theta} \cfrac{\dfrac{1}{2^4}}{1-\dfrac{1}{2}}\\ \\ &=& \cfrac{\sin ^2 2\theta}{8\theta}\\ \end{eqnarray*}
(ii)$\ \ 右の不等号の証明$
$\quad (2)より \quad 0 < x < \theta \quad のとき \quad 0 < \cfrac{\sin \theta}{\theta} < \cfrac{\sin x}{x} < 1 \quad だから \quad \cfrac{\theta}{\sin \theta} > \cfrac{x}{\sin x} $
$\qquad x=\cfrac{\theta}{2^{n-1}} \quad とおくと \quad \cfrac{\theta}{\sin \theta} > \cfrac{\dfrac{\theta}{2^{n-1}}}{\sin \dfrac{\theta}{2^{n-1}}}$
\begin{eqnarray*} S_n &=&\cfrac{\sin ^2 2\theta}{2^{2n+2}}\cdot \cfrac{2^{n-1}}{\theta} \cdot \cfrac{\dfrac{\theta}{2^{n-1}}}{\sin \dfrac{\theta}{2^{n-1}}}\\ \\ &<&\cfrac{\sin ^2 2\theta}{2^{2n+2}}\cdot \cfrac{2^{n-1}}{\theta} \cdot \cfrac{\theta}{\sin \theta} \\ \\ &=&\cfrac{\sin ^2 2\theta}{\sin \theta} \cdot \cfrac{1}{2^{n+3}}\\ \end{eqnarray*}
\begin{eqnarray*} \sum _{n=1}^\infty S_n &<&\sum _{n=1}^\infty \cfrac{\sin ^2 2\theta}{\sin \theta} \cdot \cfrac{1}{2^{n+3}}\\ \\ &=& \cfrac{\sin ^2 2\theta}{\sin \theta} \sum _{n=1}^\infty \cfrac{1}{2^{n+3}}\\ \\ &=& \cfrac{\sin ^2 2\theta}{\sin \theta} \cfrac{\dfrac{1}{2^4}}{1-\dfrac{1}{2}}\\ \\ &=& \cfrac{\sin ^2 2\theta}{8\sin \theta}\\ \end{eqnarray*}
(i),(ii)$\ より$
\[\cfrac{\sin ^2 2\theta}{8\theta} < \sum _{n=1}^{\infty} S_n < \cfrac{\sin ^2 2\theta}{8\sin \theta}\]
メインメニュー に戻る