新潟大学(理系) 2023年 問題6
$座標空間の \ 2\ 点 \ A(1,\ -1,\ 1),\ B(1,\ -1,\ 5)\ を直径の両端とする球面を \ S\ とする。次の問いに答えよ。$
$(1)\ \ 球面 \ S\ の中心 \ C\ の座標と、S\ の方程式を求めよ。$
$(2)\ \ 点 \ P\ が \ S\ 上を動くとき、\triangle ABP\ の面積の最大値を求めよ。$
$(3)\ \ 点 \ Q(x,\ y,\ z) \ が \ \angle QCA=\cfrac{\pi}{3}\ \ かつ \ \ y \geqq 0\ \ を満たしながらS上を動く。点 \ R(1+\sqrt{2},\ 0,\ 4)\ に対して、$
$\quad 内積 \ \ \vec{CQ} \cdot \vec{CR} \ \ のとりうる値の範囲を求めよ。$
(1)
$中心 \ C(x,\ y,\ z)\ は直径 \ AB\ の中点だから$
$\quad x=\cfrac{1+1}{2}=1,\qquad y=\cfrac{-1-1}{2}=-1 ,\qquad z=\cfrac{1+5}{2}=3 \qquad \therefore \ \ C(1,\ -1,\ 3)$
$AB=4 \quad だから\ \ 半径\ \ AC=2 \quad よって \quad S:(x-1)^2+(y+1)^2+(z-3)^2=4$
(2)
$\triangle ABP \ \ の辺 \ AB\ は \ S\ の直径で \ AB=4\ \ は一定である。$
$したがって \ 点 \ P\ から辺 \ AB\ に下ろした垂線の長さが高さになるので、これが最大のとき \ S\ は最大になる。$
$それは、垂線が半径 \ PC\ のときだから \quad PC=2$
$よって、面積の最大は \quad \cfrac{1}{2} \times 4 \times 2=4$
(3)
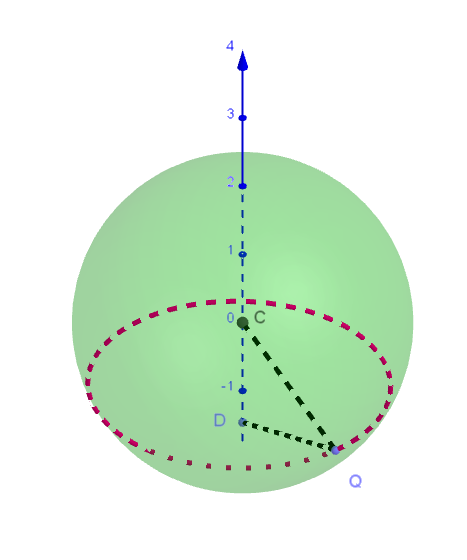
$点 \ Q\ から \ AC\ に下ろした垂線を \ QD\ とする。$
$点 \ Q\ は \ S\ 上の点だから \quad CQ=2\ \ で、\angle QCA=\cfrac{\pi}{3} \ \ だから \quad CD=1,\quad QD=\sqrt{3}$
$よって、点 \ Q\ は平面 \ z=2\ 上で、D(1,\ -1,\ 2)\ を中心に半径 \ \sqrt{3}\ の円周上にあるから$
$Q(x,\ y,\ z)\ は \quad (x-1)^2+(y+1)^2=3,\ \ z=2\ \ を満たす。$
$\quad \vec{CQ}=\vec{OQ}-\vec{OC}=(x,\ y,\ 2)-(1,\ -1,\ 3)=(x-1,\ y+1,\ -1)$
$\quad \vec{CR}=\vec{OR}-\vec{OC}=(1+\sqrt{2},\ 0,\ 4)-(1,\ -1,\ 3)=(\sqrt{2},\ 1,\ 1)$
$よって \quad \vec{CQ}\cdot \vec{CR}=\sqrt{2}(x-1)+(y+1)-1=\sqrt{2}x+y-\sqrt{2}$
$t= \vec{CQ}\cdot \vec{CR}=\sqrt{2}x+y-\sqrt{2} \quad とおくと$
\[
\hspace{1em}
\left\{ \begin{array}{l}
(x-1)^2+(y+1)^2=3 \quad (y \geqq 0) \hspace{7em}①\\
y=-\sqrt{2}x+t+\sqrt{2} \ \hspace{12em}②\\
\end{array} \right.
\]
$これを満たす \ t\ のとりうる値の範囲を求めればよいから、xy\ 平面座標で考える。$
$円①と \ x\ 軸の交点は \quad (x-1)^2+1^2=3 \quad より \quad x=1 \pm \sqrt{2}$
$\quad D(1+\sqrt{2},\ 0),\quad E(1-\sqrt{2},\ 0) \quad とおく。$
$(ア) \ \ ①と②の交点は、②を①に代入して$
$\quad (x-1)^2+(-\sqrt{2}x+t+\sqrt{2}+1)^2=3 $
$\quad 3x^2-2(1+\sqrt{2}(t+\sqrt{2}+1))x+(t+\sqrt{2}+1)^2-2=0$
$\quad 円と直線が接するとき重解をもつから$
$\quad \cfrac{D}{4}=\{1+\sqrt{2}(t+\sqrt{2}+1)\}^2 -3\{(t+\sqrt{2}+1)^2-2\}=0$
$\quad (t+\sqrt{2}+1)^2 -2\sqrt{2}(t+\sqrt{2}+1)-7=0$
$\quad t+\sqrt{2}+1 =\sqrt{2} \pm \sqrt{2+7}$
$\quad t+\sqrt{2}+1 =\sqrt{2} \pm 3$
$\quad \therefore \ \ t=2,\ \ -4$
$\quad このとき接点は \quad x=\cfrac{1+\sqrt{2}(t+\sqrt{2}+1)}{3} \quad だから$
$\quad $(i)$\ \ t=2\ \ のとき$
$\qquad x=\cfrac{1+\sqrt{2}(\sqrt{2}+3)}{3}=1+\sqrt{2}$
$\qquad y=-\sqrt{2}(1+\sqrt{2})+2+\sqrt{2}=0$
$\qquad よって \ \ 接点は \quad D(1+\sqrt{2},\ 0)\ に一致する。$
$\quad $(ii)$\ \ t=-4 \ \ のとき$
$\qquad x=\cfrac{1+\sqrt{2}(\sqrt{2}-3)}{3}=1-\sqrt{2}$
$\qquad y=-\sqrt{2}(1-\sqrt{2})-4+\sqrt{2}=-2 \quad y \geqq 0 \quad だから \ \ 不適$

$(イ) \ \ ②が点 \ E\ を通るとき$
$\quad E(1-\sqrt{2},\ 0)\ \ を②に代入して$
$\quad 0=-\sqrt{2}(1-\sqrt{2})+t+\sqrt{2} \qquad \therefore\ \ t=-2$
$以上より \quad ①と②が交点をもつのは \quad -2 \leqq t \leqq 2 \quad のとき$
$\quad したがって \quad -2 \leqq \vec{CQ}\cdot \vec{CR} \leqq 2$
メインメニュー に戻る