新潟大学(理系) 2021年 問題5
$複素数平面上の原点を中心とする単位円周上の4点 \ z_1,\ z_2,\ z_3,\ z_4\ は$
$\qquad \arg \cfrac{z_2}{z_1}=\theta _1 > 0, \quad \arg \cfrac{z_3}{z_2}=\theta _2 > 0, \quad \arg \cfrac{z_4}{z_3}=\theta _3 > 0, \quad \theta_1 + \theta_2 + \theta_3 < 2\pi $
$を満たすとする。次の問いに答えよ。$
$(1)\ \ |z_2-z_1|\ \ を \ \theta _1\ \ を用いて表せ。$
$(2)\ \ |z_3-z_1|,\quad |z_4-z_1| \ \ を \ \theta _1 ,\ \theta _2 ,\ \theta _3\ を用いて表せ。$
$(3)\ \ \cfrac{|z_4-z_1||z_2-z_1|+|z_3-z_2||z_4-z_3|}{|z_2-z_1||z_3-z_2|+|z_4-z_3||z_4-z_1|}=\cfrac{|z_3-z_1|}{|z_4-z_2|}\ \ を示せ。$
$(解説)$
$(1)\ \ \triangle OAB\ に余弦定理を用います。$
$(2)\ \ (1)と全く同様です。$
$(3)\ \ 残りの辺も(1)と同様に求めて代入しますが、三角関数の積和と和積の公式が必要になります。$
$\qquad (1),(2)とは無関係になりますが、三角形の面積公式を用いた証明を別解としました。$
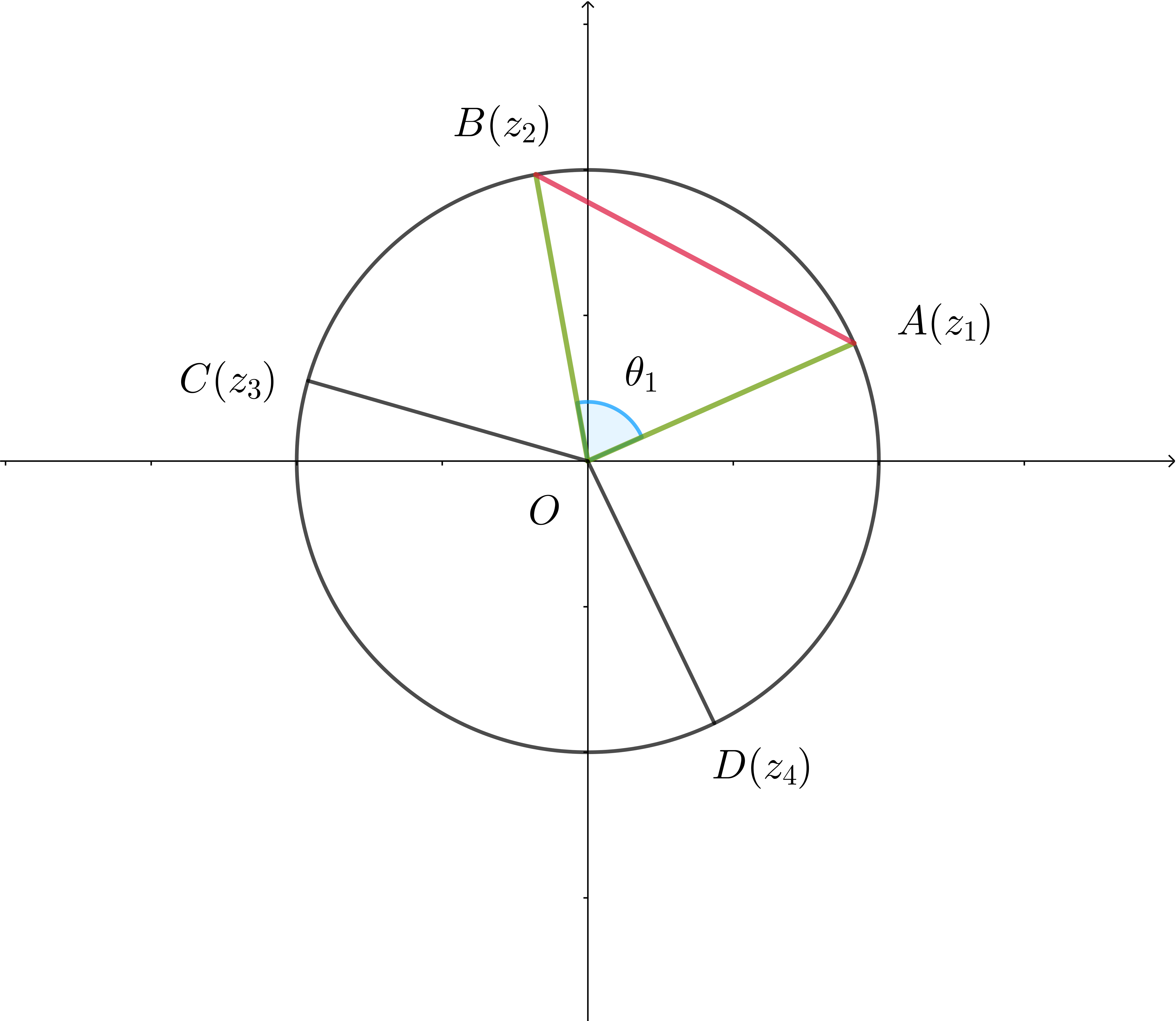
$4\ 点を \ A(z_1),\ \ B(z_2),\ \ C(z_3),\ \ D(z_4)\ とする。$
(1)
$\quad \triangle OAB\ に余弦定理を用いて$
\begin{eqnarray*} |z_2-z_1|^2 &=&AB^2\\ &=&OA^2+OB^2-2OA \cdot OB\cos \theta_1\\ &=&1^2+1^2-2 \times 1 \times 1 \times \cos \theta_1\\ &=&2(1-\cos \theta_1)\\ &=&2(1-(1-2\sin ^2\cfrac{\theta_1}{2}))\\ &=&4\sin ^2\cfrac{\theta_1}{2}\\ \end{eqnarray*} $\qquad 0 < \theta_1 < 2\pi \quad より \quad 0 < \cfrac{\theta_1}{2} < \pi \quad よって \quad \sin \cfrac{\theta_1}{2} > 0$
$\qquad \therefore \ \ |z_2-z_1|=2\sin \cfrac{\theta_1}{2}$
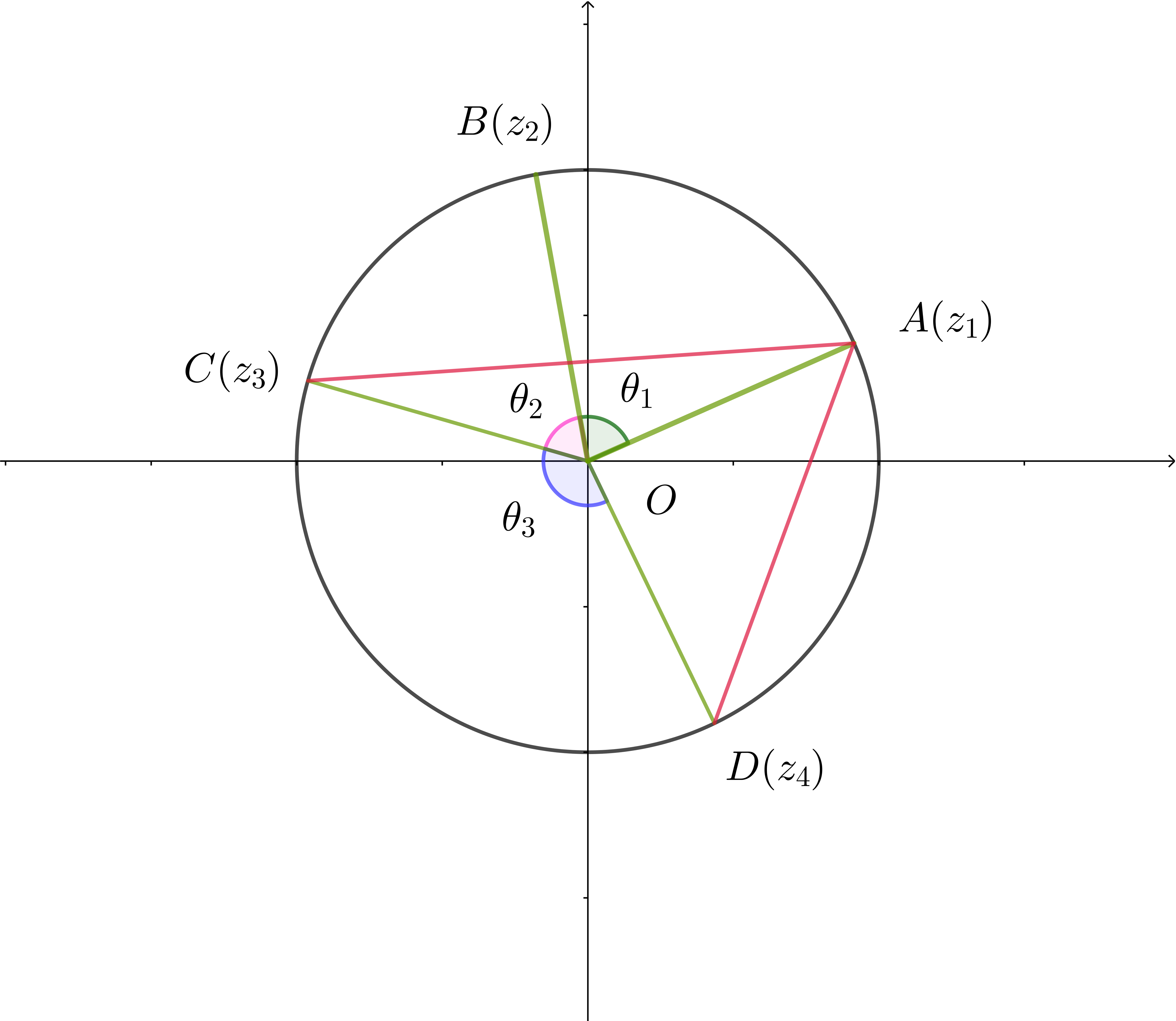
(2)
$\quad \triangle OAC\ に余弦定理を用いて$
\begin{eqnarray*} |z_3-z_1|^2 &=&AC^2\\ &=&OA^2+OC^2-2OA \cdot OC\cos (\theta_1 + \theta_2)\\ &=&1^2+1^2-2 \times 1 \times 1 \times \cos (\theta_1+\theta_2)\\ &=&2(1-\cos (\theta_1+\theta_2))\\ &=&2(1-(1-2\sin ^2\cfrac{\theta_1+\theta_2}{2}))\\ &=&4\sin ^2\cfrac{\theta_1+\theta_2}{2}\\ \end{eqnarray*} $\qquad 0 < \theta_1 +\theta_2 < 2\pi \quad より \quad 0 < \cfrac{\theta_1+\theta_2}{2} < \pi \quad よって \quad \sin \cfrac{\theta_1+\theta_2}{2} > 0$
$\qquad \therefore \ \ |z_3-z_1|=2\sin \cfrac{\theta_1+\theta_2}{2}$
$\quad \triangle OADに余弦定理を用いて$
\begin{eqnarray*} |z_4-z_1|^2 &=&AD^2\\ &=&OA^2+OD^2-2OA \cdot OD\cos (2\pi - \theta_1 - \theta_2 -\theta_3)\\ &=&1^2+1^2-2 \times 1 \times 1 \times \cos (\theta_1+\theta_2+\theta_3)\\ &=&2(1-\cos (\theta_1+\theta_2 + \theta_3))\\ &=&2(1-(1-2\sin ^2\cfrac{\theta_1+\theta_2+\theta_3}{2}))\\ &=&4\sin ^2\cfrac{\theta_1+\theta_2+\theta_3}{2}\\ \end{eqnarray*} $\qquad 0 < \theta_1 +\theta_2 +\theta_3 < 2\pi \quad より \quad 0 < \cfrac{\theta_1+\theta_2 +\theta_4}{2} < \pi \quad よって \quad \sin \cfrac{\theta_1+\theta_2+\theta_3}{2} > 0$
$\qquad \therefore \ \ |z_4-z_1|=2\sin \cfrac{\theta_1+\theta_2+\theta_3}{2}$
(3)
$(2)と全く同様にして$
$\qquad |z_3-z_2|=2\sin \cfrac{\theta_2}{2},\qquad |z_4-z_3|=2\sin \cfrac{\theta_3}{2} \quad だから$
\begin{eqnarray*} & &\cfrac{|z_4-z_1||z_2-z_1|+|z_3-z_2||z_4-z_3|}{|z_2-z_1||z_3-z_2|+|z_4-z_3||z_4-z_1|}\\ \\ &=&\cfrac{4\sin \cfrac{\theta_1+\theta_2+\theta_3}{2} \sin \cfrac{\theta_1}{2}+ 4\sin \cfrac{\theta_2}{2} \sin \cfrac{\theta_3}{2}}{ 4\sin \cfrac{\theta_1}{2} \sin \cfrac{\theta_2}{2} + 4\sin \cfrac{\theta_3}{2} \sin \cfrac{\theta_1+\theta_2+\theta_3}{2}}\\ \\ &=&\cfrac{-2\big(\cos \dfrac{2\theta_1+\theta_2+\theta_3}{2} - \cos \dfrac{\theta_2 +\theta_3}{2}\big) -2\big(\cos \dfrac{\theta_2+\theta_3}{2} -\cos \dfrac{\theta_2-\theta_3}{2}\big)}{ -2\big(\cos \dfrac{\theta_1+\theta_2}{2}- \cos \dfrac{\theta_1-\theta_2}{2}\big) - 2\big(\cos \dfrac{\theta_1+\theta_2+2\theta_3}{2}- \cos \dfrac{\theta_1+\theta_2}{2}\big) }\\ \\ &=&\cfrac{\cos \dfrac{\theta_2-\theta_3}{2} - \cos \dfrac{2\theta_1+\theta_2+\theta_3}{2}}{ \cos \dfrac{\theta_1-\theta_2}{2} - \cos \dfrac{\theta_1+\theta_2+2\theta_3}{2}}\\ \\ &=&\cfrac{-2\sin \dfrac{\theta_1+\theta_2}{2} \sin \dfrac{-\theta_1-\theta_3}{2}}{ -2\sin \dfrac{\theta_1+\theta_3}{2} \sin \dfrac{-\theta_2-\theta_3}{2}}\\ \\ &=&\cfrac{\sin \dfrac{\theta_1+\theta_2}{2}}{\sin \dfrac{\theta_2+\theta_3}{2}}\\ \end{eqnarray*} $また \quad |z_4-z_2|=2\sin \cfrac{\theta_2+\theta_3}{2} \quad だから$
$右辺=\cfrac{|z_3-z_1|}{|z_4-z_2|}=\cfrac{\sin \dfrac{\theta_1+\theta_2}{2}}{\sin \dfrac{\theta_2+\theta_3}{2}}$
$よって、右辺と左辺は一致するので等式が成りたつ。$
$(別解)$


$(1)や(2)の結果を使わない方法ですが、少しは計算が楽になります。$
$三角形の面積公式と円周角の定理を用いて$
$\quad \triangle ABD=\cfrac{1}{2}AD\cdot AB \sin \angle DAB=\cfrac{1}{2}AD\cdot AB \sin \cfrac{\angle DOB}{2}=\cfrac{1}{2}AD\cdot AB \sin \cfrac{\theta_2+\theta_3}{2} \quad より$
$\qquad AD\cdot AB =\cfrac{2}{\sin \dfrac{\theta_2+\theta_3}{2}} \triangle ABD$
$\quad \triangle BCD=\cfrac{1}{2}BC\cdot CD \sin \angle BCD=\cfrac{1}{2}BC\cdot CD \sin \cfrac{\angle BOD}{2}=\cfrac{1}{2}BC\cdot CD \sin \cfrac{2\pi-\theta_2-\theta_3}{2} \quad より$
$\qquad BC\cdot CD =\cfrac{2}{\sin \dfrac{\theta_2+\theta_3}{2}} \triangle BCD$
$\quad \triangle ABC=\cfrac{1}{2}AB\cdot BC \sin \angle ABC=\cfrac{1}{2}AB\cdot BC \sin \cfrac{\angle AOC}{2}=\cfrac{1}{2}AB\cdot BC \sin \cfrac{2\pi-\theta_1-\theta_2}{2} \quad より$
$\qquad AB\cdot BC =\cfrac{2}{\sin \dfrac{\theta_1+\theta_2}{2}} \triangle ABC$
$\quad \triangle ACD=\cfrac{1}{2}CD\cdot AD \sin \angle CDA=\cfrac{1}{2}CD\cdot AD \sin \cfrac{\angle COA}{2}=\cfrac{1}{2}CD\cdot AD \sin \cfrac{2\pi-\theta_1-\theta_2}{2} \quad より$
$\qquad CD\cdot AD =\cfrac{2}{\sin \dfrac{\theta_1+\theta_2}{2}} \triangle ACD$
$よって$
\begin{eqnarray*} & &\cfrac{|z_4-z_1||z_2-z_1|+|z_3-z_2||z_4-z_3|}{|z_2-z_1||z_3-z_2|+|z_4-z_3||z_4-z_1|}\\ \\ &=&\cfrac{AD \cdot AB + BC \cdot CD}{AB \cdot BC + CD \cdot AD}\\ \\ &=&\cfrac{\cfrac{2}{\sin \dfrac{\theta_2+\theta_3}{2}} \triangle ABD +\cfrac{2}{\sin \dfrac{\theta_2+\theta_3}{2}} \triangle BCD}{ \cfrac{2}{\sin \dfrac{\theta_1+\theta_2}{2}} \triangle ABC +\cfrac{2}{\sin \dfrac{\theta_1+\theta_2}{2}} \triangle ACD}\\ \\ &=&\cfrac{\cfrac{2}{\sin \dfrac{\theta_2+\theta_3}{2}} (\triangle ABD + \triangle BCD)}{\cfrac{2}{\sin \dfrac{\theta_1+\theta_2}{2}}(\triangle ABC + \triangle ACD)}\\ \\ &=&\cfrac{\cfrac{2}{\sin \dfrac{\theta_2+\theta_3}{2}}\square ABCD}{\cfrac{2}{\sin \dfrac{\theta_1+\theta_2}{2}}\square ABCD}\\ \\ &=&\cfrac{\sin \dfrac{\theta_1+\theta_2}{2}}{\sin \dfrac{\theta_2+\theta_3}{2}}\\ \end{eqnarray*}
メインメニュー に戻る