新潟大学(理系) 2021年 問題4
$実数 \ a\ と \ b\ に対して、関数 \ f(x)\ を \ f(x)=ax^2+bx+\cos x +2\cos \cfrac{x}{2}\ \ と定める。次の問いに答えよ。$
\[(1)\ \ \int _0^{2\pi}x\cos xdx,\quad \int _0^{2\pi}x\sin xdx \quad の値を求めよ。\]
\[(2)\ \ \int _0^{2\pi}x^2\cos xdx,\quad \int _0^{2\pi}x^2\sin xdx \quad の値を求めよ。\]
\[(3)\ \ f(x)\ が \ \ \int _0^{2\pi}f(x)\cos xdx=4+\pi,\quad \int _0^{2\pi}f(x)\sin xdx =\cfrac{4}{3}(4+\pi)\ \ を満たすとき、a\ と \ b\ の値を求めよ。\]
$\qquad (4)\ \ (3)で求めた \ a\ と \ b\ で定める \ f(x)\ に対して、f(x)\ の最小値とそのときの \ x\ の値を求めよ。$
$(解説)$
$(1)\ \ 部分積分法で求めます。$
$(2)\ \ 部分積分して、(1)をつかいます。$
$(3)\ \ (1),(2)の他、三角関数の積和の公式をつかって積分します。$
$(4)\ \ 2次式の部分と三角関数の部分に分けて、それぞれの導関数の符号をもとに \ f(x)\ の増減を調べます。$
$\qquad あるいは、それぞれの部分を平方完成する方法も考えられます。$
(1)
\[\int _0^{2\pi}x\cos xdx=\big[x\sin x \big]_0^{2\pi} -\int _0^{2\pi}\sin xdx=\big[\cos x \big]_0^{2\pi}=1-1=0\]
\[\int _0^{2\pi}x\sin xdx=\big[-x\cos x \big]_0^{2\pi} +\int _0^{2\pi}\cos xdx=-2\pi + \big[\sin x \big]_0^{2\pi}=-2\pi \]
(2)
\[\int _0^{2\pi}x^2\cos xdx=\big[x^2\sin x \big]_0^{2\pi} -\int _0^{2\pi}2x\sin xdx= -2\int _0^{2\pi}x\sin xdx=4\pi\]
\[\int _0^{2\pi}x^2\sin xdx=\big[-x^2\cos x \big]_0^{2\pi} +\int _0^{2\pi}2x\cos xdx=-4\pi^2 + 2\int _0^{2\pi}x\cos xdx=-4\pi^2\]
(3)
\begin{eqnarray*} & &\int _0^{2\pi}f(x)\cos xdx\\ \\ &=&\int _0^{2\pi}(ax^2+bx+\cos x +2\cos \cfrac{x}{2})\cos xdx\\ \\ &=&a\int _0^{2\pi}x^2\cos xdx + b\int _0^{2\pi}x\cos xdx +\int _0^{2\pi}\cos ^2x dx + 2\int _0^{2\pi} \cos \cfrac{x}{2}\cos xdx\\ \\ &=&4\pi a +\cfrac{1}{2}\int _0^{2\pi}(1+\cos 2x)dx + \int _0^{2\pi} (\cos \cfrac{3}{2}x+\cos \cfrac{1}{2}x)dx\\ \\ &=&4\pi a +\cfrac{1}{2}\big[x+\cfrac{1}{2}\sin 2x\big]_0^{2\pi} + \big[\cfrac{2}{3}\sin \cfrac{3}{2}x + 2\sin \cfrac{1}{2}x\big]_0^{2\pi} \\ \\ &=&4\pi a+ \pi \\ \end{eqnarray*}
$よって \quad 4\pi a+ \pi=4 + \pi \quad より \quad a=\cfrac{1}{\pi}$
\begin{eqnarray*} & &\int _0^{2\pi}f(x)\sin xdx\\ \\ &=&\int _0^{2\pi}(ax^2+bx+\cos x +2\cos \cfrac{x}{2})\sin xdx\\ \\ &=&a\int _0^{2\pi}x^2\sin xdx + b\int _0^{2\pi}x\sin xdx +\int _0^{2\pi}\cos x \sin x dx + 2\int _0^{2\pi} \cos \cfrac{x}{2}\sin xdx\\ \\ &=&-4\pi^2 a -2\pi b + \cfrac{1}{2}\int _0^{2\pi}\sin 2xdx + \int _0^{2\pi} (\sin \cfrac{3}{2}x+\sin \cfrac{1}{2}x)dx\\ \\ &=&-4\pi^2 a -2\pi b - \cfrac{1}{4}\big[\cos 2x\big]_0^{2\pi} + \big[-\cfrac{2}{3}\cos \cfrac{3}{2}x - 2\cos \cfrac{1}{2}x\big]_0^{2\pi} \\ \\ &=&-4\pi^2 a -2\pi b + \cfrac{16}{3} \\ \end{eqnarray*} $よって \quad -4\pi^2 a -2\pi b + \cfrac{16}{3}=\cfrac{4}{3}(4+\pi) \quad より \quad -4 \pi^2 \times \cfrac{1}{\pi} -2\pi b=\cfrac{4}{3}\pi \qquad \therefore \ \ b=-\cfrac{8}{3}$
(4)
$f(x)=\cfrac{1}{\pi}x^2 - \cfrac{8}{3}x+\cos x +2\cos \cfrac{x}{2}$
$\quad g(x)=\cfrac{1}{\pi}x^2 - \cfrac{8}{3}x ,\qquad h(x)=\cos x +2\cos \cfrac{x}{2} \quad とおくと$
$\quad g'(x)=\cfrac{2}{\pi}x - \cfrac{8}{3} ,\qquad h'(x)=-\sin x - \sin \cfrac{x}{2}=-2\sin \cfrac{3}{4}x \cos \cfrac{1}{4}x$
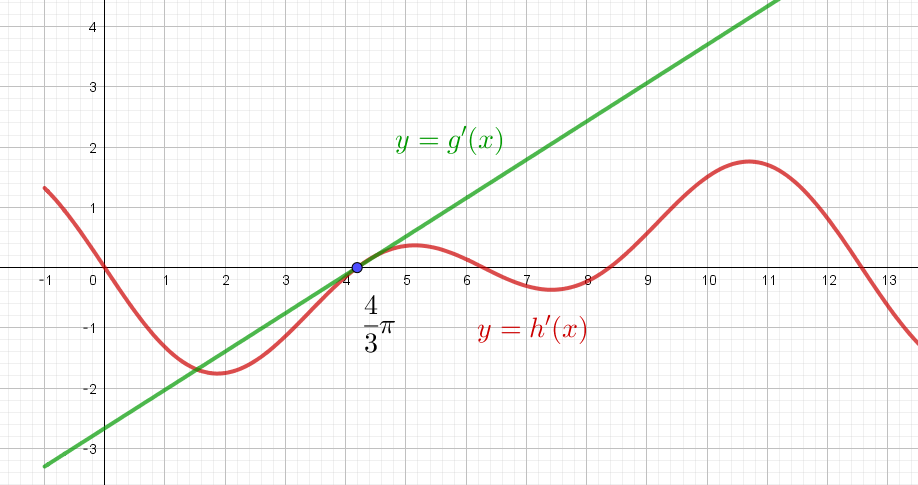
$g'(x)=0 \ の解は \quad x=\cfrac{4}{3}\pi$
$h'(x)=0 \ の解は$
$\quad \sin \cfrac{3}{4}x=0 \quad より \quad \cfrac{3}{4}x=0,\ \pi, \ 2\pi,\ 3\pi,\cdots \ \ だから$
$\qquad x=0,\ \ \cfrac{4}{3}\pi,\ \ \cfrac{8}{3}\pi,\ \ 4\pi,\ \ \cdots$
$\quad \cos \cfrac{x}{4}=0 \quad より \quad \cfrac{x}{4}=\cfrac{1}{2}\pi,\ \cfrac{3}{2}\pi, \ \cdots \ \ だから \quad x=2\pi,\ \ 6\pi, \ \ \cdots$
$y=g'(x)\ と \ y=h'(x)\ のグラフは右図のとおりで、(h'(x)\ のグラフは \ x\ 軸を切る点がわかれば概形はかける)$
$f'(x)=g'(x)+h'(x) \ \ であるから \ f'(x)\ の符号を調べた増減表は$
\[
\begin{array}{c||c|c|c|c|c}
\hline
x & \cdots & \cfrac{4}{3}\pi & \cdots \\
\hline
f'(x) & - & 0 & + \\
\hline
f(x) & \searrow & 極小 & \nearrow \\
\end{array}
\]
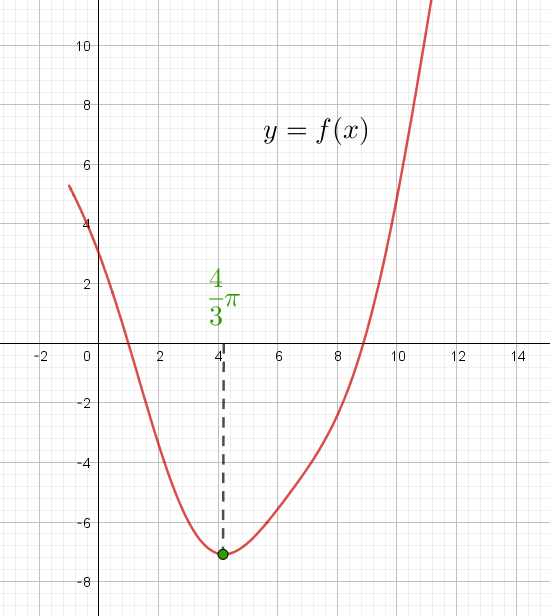
$f(x)\ は \ \ x =\cfrac{4}{3}\pi \ \ で極小かつ最小となる。$
$最小値は \quad f(\cfrac{4}{3}\pi)=\cfrac{1}{\pi}(\cfrac{4}{3}\pi)^2 - \cfrac{8}{3} \times \cfrac{4}{3}\pi +\cos \cfrac{4}{3}\pi +2\cos \cfrac{2}{3}\pi=-\cfrac{16}{9}\pi - \cfrac{3}{2}$
$なお、グラフは右のとおりです。$
$(別解)$
\begin{eqnarray*}
f(x)
&=&\cfrac{1}{\pi}x^2 - \cfrac{8}{3}x+\cos x +2\cos \cfrac{x}{2}\\
\\
&=&\cfrac{1}{\pi}(x^2 - \cfrac{8}{3}\pi x) + (2\cos ^2 \cfrac{x}{2} -1) + 2\cos \cfrac{x}{2}\\
\\
&=&\cfrac{1}{\pi}(x - \cfrac{4}{3}\pi)^2-\cfrac{16}{9}\pi + 2(\cos \cfrac{x}{2} +\cfrac{1}{2})^2 -\cfrac{3}{2}\\
\\
&=&\cfrac{1}{\pi}(x - \cfrac{4}{3}\pi)^2 + 2(\cos \cfrac{x}{2} +\cfrac{1}{2})^2 -\cfrac{16}{9}\pi -\cfrac{3}{2}\\
\\
\end{eqnarray*}
$ここで、第\ 1\ 項を \ 0\ とする \ \ x =\cfrac{4}{3}\pi \ \ は \ \ 第 \ 2\ 項=(\cos \cfrac{x}{2} +\cfrac{1}{2})^2=(\cos \cfrac{2}{3}\pi +\cfrac{1}{2})^2=0 \quad となるから$
$f(x)\ は \ \ x =\cfrac{4}{3}\pi\ \ で最小となり、最小値は \quad -\cfrac{16}{9}\pi -\cfrac{3}{2}$
$(注意)$
$(x - \cfrac{4}{3}\pi)^2 +(\cos \cfrac{x}{2} +\cfrac{1}{2})^2 \ \ のような同じ変数 \ x\ の \ 2\ 項の平方完成のこの方法は、たまたま同時に \ 0\ にする$
$xの値が存在したから使えましたが、本来は独立な \ 2\ 変数で使う手法です。$
メインメニュー に戻る