新潟大学(理系) 2021年 問題2
$座標平面上の \ 2\ 点 \ A(0,\ -1),\ B(1,\ 2)\ を通る直線を \ l\ とする。また、中心 \ (3,\ -2),半径 \ 3\ の円を \ C\ とする。$
$次の問いに答えよ。$
$(1)\ \ l\ の方程式を求めよ。$
$(2)\ \ l\ と \ C\ は共有点を持たないことを示せ。$
$(3)\ \ 点 \ Pが円 \ C\ 上を動くとき、三角形 \ ABP\ の重心の軌跡を \ T\ とする。T\ はどのような図形になるか答えよ。$
$(4)\ \ (3)で求めた 図形 \ T\ 上の点 \ (x,\ y)\ に対して、 \sqrt{x^2+y^2}\ \ の最大値と最小値を求めよ。$
$(解説)$
$(1)\ \ 確実に点がとれる問題です。逆にこの設問はいらないですね。$
$(2)\ \ 円と直線の位置関係の問題です。円の中心と直線との距離と円の半径の大小で調べます。$
$(3)\ \ P(a,\ b),\ 重心を \ G(x,\ y) \ \ とおいて、a,\ b\ を \ x,\ y\ の式で表します。点 \ P\ は円 \ C\ 上にあります。$
$(4)\ \ \sqrt{x^2+y^2}\ \ は原点と点 \ (x,\ y)\ の距離です。$
(1)
$\quad 傾き=\cfrac{2-(-1)}{1-0}=3,\qquad 点 \ A(0,\ -1)\ を通るから \qquad l:y=3x-1$
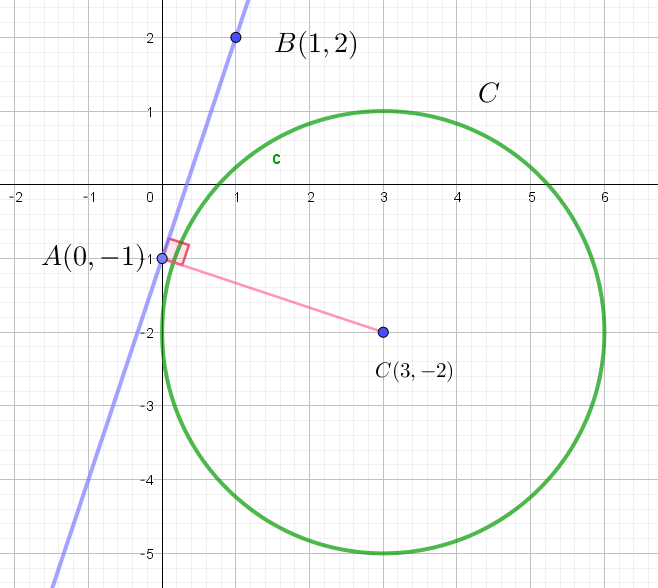
(2)
$\quad 直線 \ l :3x-y-1=0\ \ と \ 中心 \ C(3,\ -2)\ の距離 \ d\ は$
$\qquad d=\cfrac{|3 \times 3 -(-2)-1|}{\sqrt{3^2+(-1)^2}}=\cfrac{10}{\sqrt{10}}=\sqrt{10}$
$\quad 円 \ C\ の半径 \ r\ は \ \ r=3\ \ で、 d >r \ \ だから直線 \ l\ と円 \ C\ は$
$\quad 共有点を持たない。$
(3)
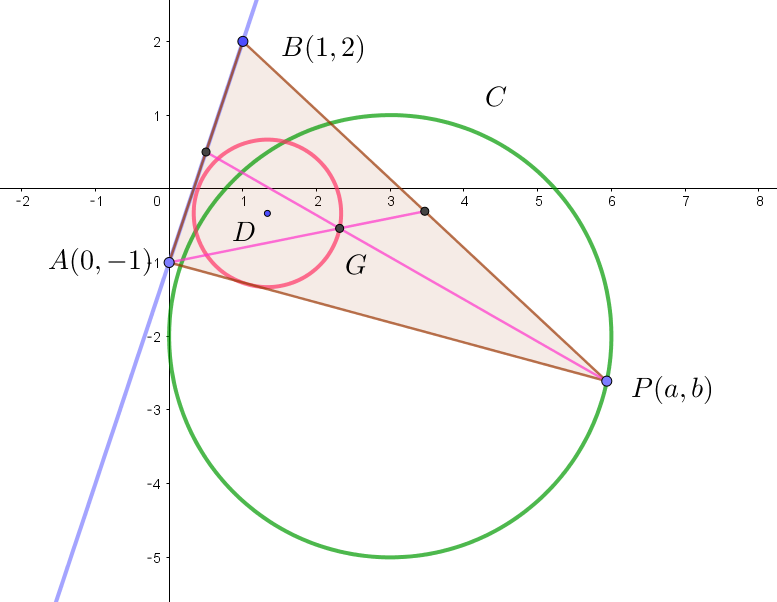
$P(a,\ b)\ \ とおくと \quad (a-3)^2+(b+2)^2=9 \hspace{5em}①$
$\triangle ABP \ \ の重心 \ G(x,\ y)は$
$\qquad x=\cfrac{0+1+a}{3}=\cfrac{a+1}{3}$
$\qquad y=\cfrac{-1+2+b}{3}=\cfrac{b+1}{3}$
$\quad a=3x-1,\quad b=3y-1 \quad を①に代入して$
$\quad (3x-4)^2+(3y+1)^2=9$
$\quad (x-\cfrac{4}{3})^2+(y+\cfrac{1}{3})^2=1$
$よって T\ は、中心 \ D(\cfrac{4}{3},\ -\cfrac{1}{3}),\ \ 半径 \ 1\ の円である。$
(4)
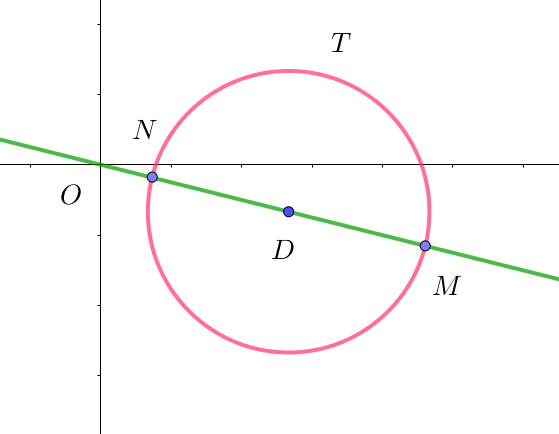
$t=\sqrt{x^2+y^2} \ \ は原点 \ O\ と \ T\ 上の点 \ (x,\ y)\ との距離だから$
$最大値、最小値をとる点 \ M,\ N \ は、直線 \ OD \ と円 \ T\ の交点である。$
$\qquad OD=\sqrt{(\cfrac{4}{3})^2+(-\cfrac{1}{3})^2}=\sqrt{\cfrac{17}{9}}=\cfrac{\sqrt{17}}{3}$
$\quad 最大値は \quad OM=OD+Tの半径=\cfrac{\sqrt{17}}{3}+1=\cfrac{\sqrt{17}+3}{3}$
$\quad 最小値は \quad ON=OD-Tの半径=\cfrac{\sqrt{17}}{3}-1=\cfrac{\sqrt{17}-3}{3}$
$なお、直線 \ OD\ のパラメータ表示は$
$\quad x=\cfrac{4}{3}k,\quad y=-\cfrac{1}{3}k \quad とおけるから円 \ T\ との交点は$
$\quad (\cfrac{4}{3}k-\cfrac{4}{3})^2+(-\cfrac{1}{3}k+\cfrac{1}{3})^2=1$
$\quad \cfrac{16}{9}(k-1)^2+\cfrac{1}{9}(k-1)^2=1$
$\quad \cfrac{17}{9}(k-1)^2 =1 \qquad \therefore \ \ k=1 \pm \cfrac{3}{\sqrt{17}}=\cfrac{17 \pm 3\sqrt{17}}{17}$
$よって$
$\quad 最大値をとる点 \ M\ は \quad x=\cfrac{4}{3} \times \cfrac{17 + 3\sqrt{17}}{17}=\cfrac{4(17 + 3\sqrt{17})}{51},\quad y=-\cfrac{1}{3} \times \cfrac{17 + 3\sqrt{17}}{17}=-\cfrac{17 + 3\sqrt{17}}{51}$
$\quad 最小値をとる点 \ N\ は \quad x=\cfrac{4}{3} \times \cfrac{17 - 3\sqrt{17}}{17}=\cfrac{4(17 - 3\sqrt{17})}{51},\quad y=-\cfrac{1}{3} \times \cfrac{17 - 3\sqrt{17}}{17}=-\cfrac{17 - 3\sqrt{17}}{51}$
メインメニュー に戻る