新潟大学(理系) 2021年 問題1
$正四面体 \ OABC\ において三角形 \ ABC\ の重心を \ D,\ 線分 \ AB\ を \ 2:1\ に内分する点を \ E,\ 線分 \ AC\ を$
$5:2\ に外分する点を \ F\ とする。\vec{OA}=\vec{a},\ \ \vec{OB}=\vec{b},\ \ \vec{OC}=\vec{c}\ \ として、次の問いに答えよ。$
$(1)\ \ ベクトル \ \vec{OE}\ および \ \vec{OF}\ を \ \vec{a},\ \vec{b},\ \vec{c}\ を用いて表せ。$
$(2)\ \ ベクトル \ \vec{OD}\ を \ \vec{a},\ \vec{b},\ \vec{c}\ を用いて表せ。$
$(3)\ \ 点 \ G\ は点 \ E\ を通り \ \ \vec{OA}\ に平行な直線上にある。点 \ H\ は点 \ F\ を通り \ \ \vec{OB}\ に平行な直線上にある。$
$\qquad 3\ 点D,\ G,\ H\ が一直線上にあるとき、ベクトル \ \ \vec{OG}\ および \ \vec{OH}\ を \ \vec{a},\ \vec{b},\ \vec{c}\ を用いて表せ。$
$(4)\ \ (3)で求めた \ \ \vec{OG},\ \vec{OH}\ に対して、\cfrac{|\vec{OH}|^2}{|\vec{OG}|^2}\ \ を求めよ。$
$(解説)$
$(1)\ \ 結論だけ書いても点数はもらえるでしょうか。不安ですね。$
$(2)\ \ 内分点、外分点の位置ベクトルを求める基本問題です。$
$(3)\ \ 直線のベクトル方程式と3点が一直線上にあるベクトル表現をつかいます。$
$(4)\ \ 正四面体の4つの面は正三角形です。$
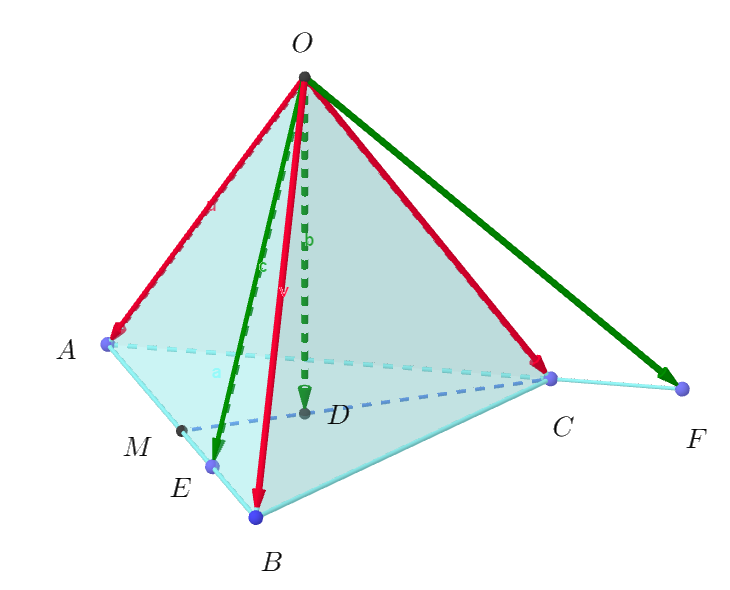
(1)
$辺 \ AB\ の中点を \ M\ とすると \qquad \vec{OM}=\cfrac{\vec{a}+\vec{b}}{2}$
$重心\ D\ は線分 \ CM\ を \ 2:1\ に内分する点だから$
$\quad \vec{OD}=\cfrac{\vec{OC}+2\vec{OM}}{3}=\cfrac{1}{3}\vec{a}+\cfrac{1}{3}\vec{b}+\cfrac{1}{3}\vec{c}$
(2)
(i)$\ \ 点 \ E\ は線分 \ AB\ を \ 2:1\ に内分する点だから$
$\qquad \vec{OE}=\cfrac{\vec{OA}+2\vec{OB}}{3}=\cfrac{1}{3}\vec{a}+\cfrac{2}{3}\vec{b}$
(ii)$\ \ 点 \ F\ は線分 \ AC\ を \ 5:2\ に外分する点だから$
$\qquad \vec{OF}=\cfrac{-2\vec{OA}+5\vec{OC}}{5-2}=-\cfrac{2}{3}\vec{a}+\cfrac{5}{3}\vec{c}$
(3)
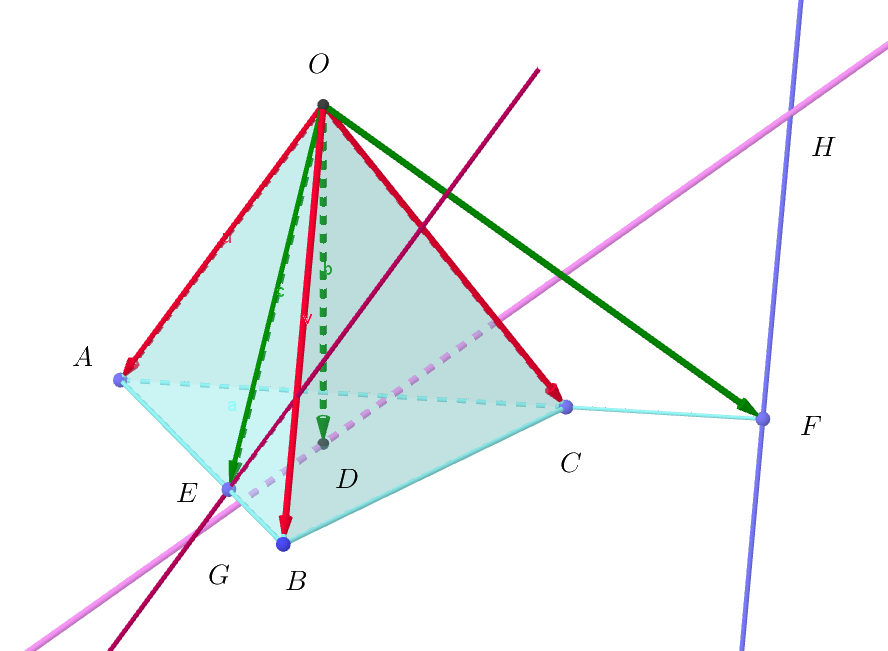
$点 \ G\ は点 \ E\ を通り \ \ \vec{OA}\ に平行な直線上にあるから$
$\quad \vec{OG}=\vec{OE}+s\vec{OA}=\cfrac{1}{3}\vec{a}+\cfrac{2}{3}\vec{b} + s\vec{a}=(\cfrac{1}{3}+s)\vec{a}+\cfrac{2}{3}\vec{b} \ \ (s は実数)$
$点 \ H\ は点 \ F\ を通り \ \ \vec{OB}\ に平行な直線上にあるから$
$\quad \vec{OH}=\vec{OF}+t\vec{OB}=-\cfrac{2}{3}\vec{a} +\cfrac{5}{3}\vec{c}+t\vec{b}=-\cfrac{2}{3}\vec{a}+t\vec{b}+\cfrac{5}{3}\vec{c}\ \ (tは実数)$
$3\ 点D,\ G,\ H\ が一直線上にあるから \quad \vec{DG}=u\vec{DH} \ \ (uは実数)とおける。$
$\quad \vec{OG}-\vec{OD}=u(\vec{OH}-\vec{OD})$
$\quad (\cfrac{1}{3}+s)\vec{a}+\cfrac{2}{3}\vec{b} -(\cfrac{1}{3}\vec{a}+\cfrac{1}{3}\vec{b}+\cfrac{1}{3}\vec{c})
=u(-\cfrac{2}{3}\vec{a}+t\vec{b}+\cfrac{5}{3}\vec{c}-(\cfrac{1}{3}\vec{a}+\cfrac{1}{3}\vec{b}+\cfrac{1}{3}\vec{c}) \big)$
$\quad s\vec{a}+\cfrac{1}{3}\vec{b} -\cfrac{1}{3}\vec{c}=-u\vec{a}+u(t-\cfrac{1}{3})\vec{b}+\cfrac{4}{3}u\vec{c}$
$\quad \vec{a},\ \ \vec{b},\ \ \vec{c}\ \ は \ \vec{0}\ でなく、互いに平行でない(一次独立)から$
\[
\hspace{1em}
\left\{ \begin{array}{l}
s=-u \\
\cfrac{1}{3}=u(t-\cfrac{1}{3}) \\
-\cfrac{1}{3}=\cfrac{4}{3}u \\
\end{array} \right.
\]
$これを解いて \qquad s=\cfrac{1}{4},\quad t=-1,\quad u=-\cfrac{1}{4}$
$よって \quad \vec{OG}=\cfrac{7}{12}\vec{a}+\cfrac{2}{3}\vec{b},\qquad \vec{OH}=-\cfrac{2}{3}\vec{a} -\vec{b}+\cfrac{5}{3}\vec{c}$
(4)
$正四面体 \ OABC\ の辺の長さを \ p\ とおくと、|\vec{a}|=|\vec{b}|=|\vec{c}|=p$
$4\ つの各面は正三角形だから、\quad \vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}|\cos 60°=\cfrac{1}{2}p^2$
$同様にして、\quad \vec{b} \cdot \vec{c}=\vec{c} \cdot \vec{a}=\cfrac{1}{2}p^2$
$したがって$
\begin{eqnarray*} |\vec{OG}|^2 &=&\big|\cfrac{7}{12}\vec{a}+\cfrac{2}{3}\vec{b}\big|^2\\ \\ &=&\cfrac{49}{144}|\vec{a}|^2+\cfrac{7}{9}\vec{a}\cdot \vec{b}+\cfrac{4}{9}|\vec{b}|^2\\ \\ &=&\cfrac{49}{144}p^2+\cfrac{7}{9} \times \cfrac{1}{2}p^2 +\cfrac{4}{9}p^2\\ \\ &=&\cfrac{169}{144}p^2 \end{eqnarray*}
\begin{eqnarray*} |\vec{OH}|^2 &=&\big|-\cfrac{2}{3}\vec{a}-\vec{b}+\cfrac{5}{3}\vec{c}\big|^2\\ \\ &=&\cfrac{4}{9}|\vec{a}|^2+|\vec{b}|^2+\cfrac{25}{9}|\vec{c}|^2+\cfrac{4}{3}\vec{a}\cdot \vec{b}-\cfrac{10}{3}\vec{b}\cdot \vec{c}-\cfrac{20}{9}\vec{c}\cdot \vec{a}\\ \\ &=&\cfrac{4}{9}p^2+p^2+\cfrac{25}{9}p^2+\cfrac{4}{3}\times \cfrac{1}{2}p^2 -\cfrac{10}{3} \times \cfrac{1}{2}p^2 -\cfrac{20}{9} \times \cfrac{1}{2}p^2\\ \\ &=&\cfrac{19}{9}p^2 \end{eqnarray*}
$\qquad \therefore \ \ \cfrac{|\vec{OH}|^2}{|\vec{OG}|^2}=\cfrac{\dfrac{19}{9}p^2}{\dfrac{169}{144}p^2}=\cfrac{304}{169}$
メインメニュー に戻る