名古屋大学(理系) 2024年 問題3
$座標空間の \ 3\ 点A(3,\ 1,\ 3),\ \ B(4,\ 2,\ 2),\ \ C(4,\ 0,\ 1)\ \ の定める平面を \ H\ とする。また、\vec{AP}=s\vec{AB}+t\vec{AC}$
$(s,\ t\ は非負の実数)を満たすすべての点 \ P\ からなる領域を \ K\ とする。$
$(1)\ \ 内積 \ \vec{AB}\cdot \vec{AB},\ \ \vec{AC}\cdot \vec{AC},\ \ \vec{AB}\cdot \vec{AC}\ \ を求めよ。$
$(2)\ \ 原点O(0,\ 0,\ 0)\ \ から平面 \ H\ に下ろした垂線の足を \ Q\ とする。\vec{AQ}\ を \ \vec{AB}\ と \ \vec{AC}\ で表せ。$
$(3)\ \ 領域 \ K\ 上の点P\ に対して、線分 \ QP\ 上の点で \ \vec{AR}=r\vec{AC}\ \ (r\ は非負の実数)を満たす点R\ が存在する$
$\quad ことを示せ。$
$(4)\ \ 領域 \ K\ において原点 \ O\ からの距離が最小となる点 \ S\ の座標を求めよ。$
(1)
$\vec{AB}=(4,\ 2,\ 2)-(3,\ 1,\ 3)=(1,\ 1,\ -1),\quad \vec{AC}=(4,\ 0,\ 1)-(3,\ 1,\ 3)=(1,\ -1,\ -2)\quad より$
$\vec{AB}\cdot \vec{AB}=(1,\ 1,\ -1) \cdot (1,\ 1,\ -1)=1+1+1=3$
$\vec{AC}\cdot \vec{AC}=(1,\ -1,\ -2) \cdot (1,\ -1,\ -2)=1+1+4=6$
$\vec{AB}\cdot \vec{AC}=(1,\ 1,\ -1) \cdot (1,\ -1,\ -2)=1-1+2=2$
(2)
$4\ 点 \ A,\ B,\ C,\ Q\ は平面 \ H\ 上にあるから $
$\vec{AQ}=k\vec{AB}+\ell \vec{AC} \ \ (k,\ l\ は実数)\ \ とおける。$
$\vec{AQ} \cdot \vec{AB}=(k\vec{AB}+\ell \vec{AC})\cdot \vec{AB}=k\vec{AB} \cdot \vec{AB} +\ell \vec{AC}\cdot \vec{AB}=3k+2\ell$
$\vec{AQ} \cdot \vec{AC}=(k\vec{AB}+\ell \vec{AC})\cdot \vec{AC}=k\vec{AB} \cdot \vec{AC} +\ell \vec{AC}\cdot \vec{AC}=2k+6\ell$
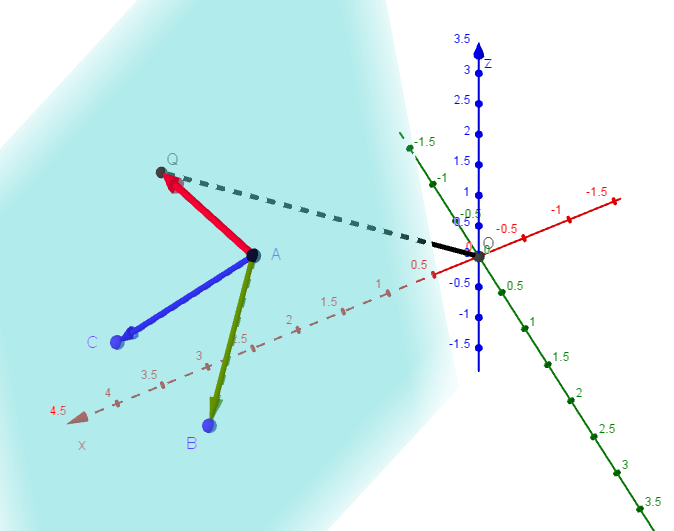
$\vec{OQ} \perp \ \ 平面 \ H \quad より$
(i)$\ \ \vec{OQ}\perp \vec{AB}$
$\quad \vec{OQ}\cdot \vec{AB}=0$
$\quad (\vec{AQ}-\vec{AO})\cdot \vec{AB}=0$
$\quad \vec{AQ}\cdot \vec{AB} + \vec{OA}\cdot \vec{AB}=0$
$\quad 3k+2\ell + (3,\ 1,\ 3)\cdot (1,\ 1,\ -1)=0$
$\quad 3k+2\ell =-1 \hspace{5em}①$
(ii)$\ \ \vec{OQ}\perp \vec{AC}$
$\quad \vec{OQ}\cdot \vec{AC}=0$
$\quad (\vec{AQ}-\vec{AO})\cdot \vec{AC}=0$
$\quad \vec{AQ}\cdot \vec{AC} + \vec{OA}\cdot \vec{AC}=0$
$\quad 2k+6\ell + (3,\ 1,\ 3)\cdot (1,\ -1,\ -2)=0$
$\quad 2k+6\ell =4$
$\quad k+3\ell =2 \hspace{5em}②$
$①②を解いて \quad k=-1,\quad \ell=1$
$したがって \quad \vec{AQ}=-\vec{AB}+ \vec{AC}$
(3)

$\vec{AP}=s\vec{AB}+t\vec{AC} \ \ (s,\ t\ は非負の実数)$
$(2)より \quad \vec{AQ}=-\vec{AB}+ \vec{AC}=\vec{BC}$
\begin{eqnarray*}
\vec{QP}
&=&\vec{AP}-\vec{AQ}\\
\\
&=&(s\vec{AB}+t\vec{AC})-(-\vec{AB}+\vec{AC})\\
\\
&=&(s+1)\vec{AB}+(t-1)\vec{AC}\\
\end{eqnarray*}
$点\ R\ は線分 \ QP\ 上の点だから、\vec{QR}=k\vec{QP}\ \ を満たす実数 \ k\ が存在する。$
$\vec{QR}=k\vec{QP}=k(s+1)\vec{AB}+k(t-1)\vec{AC}$
\begin{eqnarray*}
\vec{AR}
&=&\vec{QR}-\vec{QA}\\
\\
&=&k(s+1)\vec{AB}+k(t-1)\vec{AC}+\vec{AQ}\\
\\
&=&k(s+1)\vec{AB}+k(t-1)\vec{AC}+\vec{BC}\\
\\
&=&k(s+1)\vec{AB}+k(t-1)\vec{AC}+(\vec{AC}-\vec{AB})\\
\\
&=&(k(s+1)-1)\vec{AB}+(k(t-1)+1)\vec{AC}\\
\end{eqnarray*}
$ここで、k(s+1)=1 \qquad k=\cfrac{1}{s+1} \quad ととると$
$\vec{AR}=(k(t-1)+1)\vec{AC}=(\cfrac{t-1}{s+1}+1)\vec{AC} =\cfrac{s+t}{s+1}\vec{AC} \quad だから$
$r=\cfrac{s+t}{s+1} \quad とおくと \quad \vec{AR}=r\vec{AC}\ \ ただし \ r\ は非負の実数とおける。$
(4)
$直角三角形\ OQP \ \ において \ \ OP\ は斜辺だから \ \ QP \leqq OP$
$(3)の点 \ R\ の取り方から \quad QR \leqq QP $
$直線 \ AC\ 上の点で、QR\ が最小になる点は、点 \ Q\ から直線 \ AC\ に下ろした垂線との交点であるから$
$この点が求める点 \ S\ となる。$
$\vec{AS}=r\vec{AC} \quad とおけて \quad \vec{QS} \perp \vec{AC} \quad より$
$(\vec{AS}-\vec{AQ})\cdot \vec{AC}=0$
$(r\vec{AC}-\vec{BC})\cdot \vec{AC}=0$
$r\vec{AC} \cdot \vec{AC} -\vec{BC}\cdot \vec{AC}=0$
$6r-(0,\ -2,\ -1) \cdot (1,\ -1,\ -2)=0$
$6r-4=0$
$r=\cfrac{2}{3}$
$\vec{AS}=\cfrac{2}{3}\vec{AC}$
$\vec{OS}-\vec{OA}=\cfrac{2}{3}\vec{AC}$
$\vec{OS}=\vec{OA}+\cfrac{2}{3}\vec{AC}=(3,\ 1,\ 3)+\cfrac{2}{3}(1,\ -1,\ -2)=(\cfrac{11}{3},\ \cfrac{1}{3},\ \cfrac{5}{3})$
$\therefore \ \ S(\cfrac{11}{3},\ \cfrac{1}{3},\ \cfrac{5}{3})$
メインメニュー に戻る