名古屋大学(理系) 2021年 問題4
$0 \leqq a < 1 \ \ を満たす実数 \ a\ に対し、数列 \ \{a_n\}\ を \ \ a_1=a,\ \ a_{n+1}=3[a_n+\cfrac{1}{2}]-2a_n \ \ (n=1,\ 2,\ 3,\ \cdots )\ という$
$漸化式で定める。ただし、[x]\ は \ x\ 以下の最大の整数を表す。以下の問に答えよ。$
$(1)\ \ a\ が \ 0 \leqq a < 1 \ \ の範囲を動くとき、点\ (x,\ y)=(a_1,\ a_2)\ \ の軌跡を \ xy\ 平面上に図示せよ。$
$(2)\ \ a_n - [a_n] \geqq \cfrac{1}{2}\ \ ならば、a_n < a_{n+1}\ \ であることを示せ。$
$(3)\ \ a_n > a_{n+1} \ \ ならば、a_{n+1}=3[a_n]-2a_n \ \ かつ \ \ [a_{n+1}]=[a_n]-1\ \ であることを示せ。$
$(4)\ \ ある \ 2\ 以上の自然数 \ k\ に対して、a_1 > a_2 > \cdots > a_k \ \ が成り立つとする。このとき \ a_k \ を \ a\ の式で表せ。$
$(解説)$
$(1)\ \ ガウス記号は、場合分けして \ [ ]\ をはずします。$
$(2)\ \ a_n=b_n+r_n \ \ (b_n \ \ は整数、\ \ 0 \leqq r_n < 1) \ \ とおきます。$
$(3)\ \ (2)のようにおいて、場合分けして \ [ ]\ をはずします。$
$(4)\ \ (3)の2つの漸化式を解きます。$
(1)
$\quad a_2=3[a_1+\cfrac{1}{2}]-2a_1 \quad だから \quad y=3[x+\cfrac{1}{2}]-2x $
$\quad ただし、0 \leqq a <1 \ \ で \ \ x=a_1=a \quad だから \quad 0 \leqq x < 1$
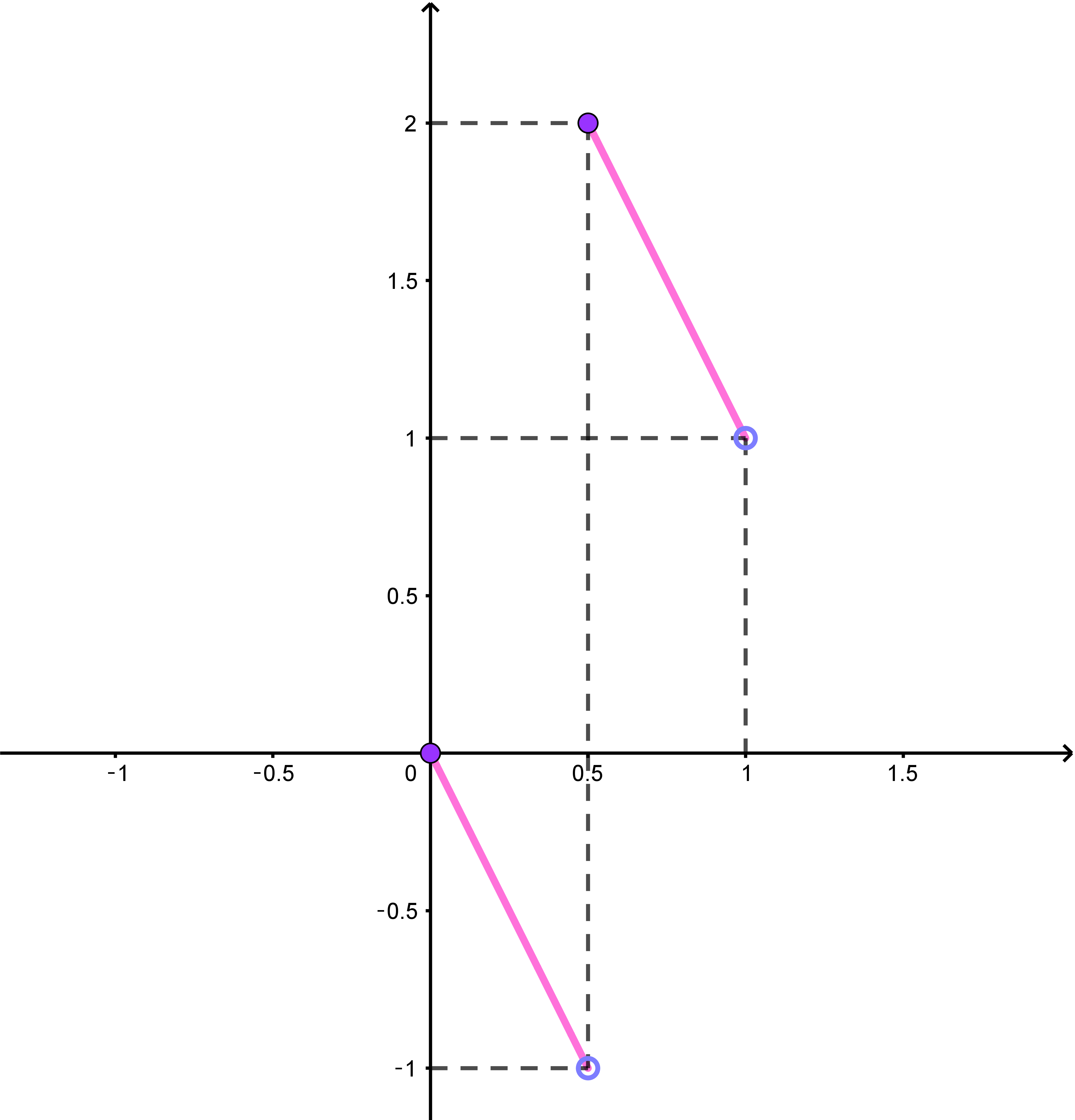
(i)$\ \ 0 \leqq x <\cfrac{1}{2} \quad のとき$
$\quad \cfrac{1}{2} \leqq x +\cfrac{1}{2} <1 \quad だから \quad [x+\cfrac{1}{2} ]=0$
$\quad \therefore \ \ y=-2x$
(ii)$\ \ \cfrac{1}{2} \leqq x < 1 \quad のとき$
$\quad 1 \leqq x +\cfrac{1}{2} < \cfrac{3}{2} \quad だから \quad [x+\cfrac{1}{2} ]=1$
$\quad \therefore \ \ y=3-2x$
(2)
$\quad a_n=b_n+r_n \ \ (b_n \ \ は整数、\ \ 0 \leqq r_n < 1) \ \ とおくと$
$\quad a_n - [a_n] \geqq \cfrac{1}{2} \quad より \quad b_n +r_n -[ b_n +r_n] \geqq \cfrac{1}{2}$
$\quad b_n +r_n - b_n \geqq \cfrac{1}{2} \qquad \therefore \ \ \cfrac{1}{2} \leqq r_n <1 $
$このとき$
\begin{eqnarray*} a_{n+1}-a_n &=&\big\{3[a_n + \cfrac{1}{2}]-2a_n\big\} -a_n\\ \\ &=&3\big\{[a_n + \cfrac{1}{2}]-a_n\big\} \\ \\ &=&3\big\{[b_n + r_n +\cfrac{1}{2}]- (b_n + r_n)\big\} \\ \\ &=&3\big\{[b_n +1+ r_n - \cfrac{1}{2}]- (b_n + r_n)\big\} \hspace{3em} \big(0 \leqq r_n -\cfrac{1}{2} < \cfrac{1}{2} \big)\\ \\ &=&3\{(b_n +1)- (b_n + r_n)\} \\ \\ &=&3(1- r_n)\\ \\ &>&0 \end{eqnarray*} $\quad よって \quad a_n < a_{n+1}$
(3)
$\quad a_n > a_{n+1} \quad ならば \quad a_n > 3[a_n+\cfrac{1}{2}]-2a_n \qquad \therefore \ \ a_n > [a_n+\cfrac{1}{2}]$
$\quad a_n=b_n+r_n \ \ (b_n \ \ は整数、\ \ 0 \leqq r_n < 1) \ \ とおくと \quad b_n+r_n > [b_n+r_n +\cfrac{1}{2}]$
(i)$\ \ 0 \leqq r_n <\cfrac{1}{2} \quad のとき$
$\quad \cfrac{1}{2} \leqq r_n +\cfrac{1}{2} <1 \quad だから \quad [b_n+r_n +\cfrac{1}{2} ]=b_n$
$\quad よって \qquad b_n+r_n > b_n \quad となり \quad r_n > 0$
(ii)$\ \ \cfrac{1}{2} \leqq r_n < 1 \quad のとき$
$\quad 0 \leqq r_n -\cfrac{1}{2} < \cfrac{1}{2} \quad だから \quad [b_n+r_n+\cfrac{1}{2} ]=[b_n+1+r_n-\cfrac{1}{2} ]=b_n+1$
$\quad よって \qquad b_n+r_n > b_n +1 \quad となり \quad r_n > 1 \quad これは矛盾である。$
$\quad したがって \quad $(i)$より 0 < r_n < \cfrac{1}{2} \qquad このとき \quad \cfrac{1}{2} < r_n +\cfrac{1}{2} < 1 \quad だから$
$\quad [a_n+\cfrac{1}{2}]=[b_n+r_n + \cfrac{1}{2}]=b_n=[a_n]$
$\quad よって \quad a_{n+1}=3[a_n+\cfrac{1}{2}]-2a_n=3[a_n]-2a_n$
$\quad さらに続けて$
\begin{eqnarray*} a_{n+1} &=&3[a_n]-2a_n\\ \\ &=&3b_n -2(b_n + r_n)\\ \\ &=&b_n -2r_n\\ \\ &=&b_n -1 +(1-2r_n) \qquad \big(0 < 1-2r_n <1 \big)\\ \end{eqnarray*} $\quad よって \quad [a_{n+1}]= b_n -1 =[a_n]-1$
(4)
$\quad a_1 > a_2 > \cdots > a_k \ \ が成り立つから、k \geqq 2 \ \ の \ k\ に対して(3)の \ 2\ つの漸化式が成りたつ。$
$\quad [a_{n+1}]= [a_n]-1 \quad より \quad [a_n]\ \ は初項 \ \ [a_1]=[a]=0,\quad 公差 \ \ -1 \ の等差数列だから$
$\qquad [a_n]=(n-1)(-1)=1-n$
$\quad a_{n+1}= 3[a_n]-2a_n \quad より \quad a_{n+1}= 3(1-n)-2a_n=-2a_n+3(1-n)$
$\quad 漸化式 \quad a_{n+1}= -2a_n+3(1-n) \quad を解くために \quad 両辺を \ \ (-2)^{n+1}\ \ で割って$
$\qquad \cfrac{a_{n+1}}{(-2)^{n+1}}= \cfrac{a_n}{(-2)^n} + \cfrac{3(1-n)}{(-2)^{n+1}}$
$\qquad c_n=\cfrac{a_n}{(-2)^n} ,\qquad f(n)=\cfrac{3(1-n)}{(-2)^{n+1}} \quad とおくと \qquad c_1=\cfrac{a_1}{-2}=-\cfrac{a}{2}$
$\qquad c_{n+1}=c_n+ f(n) \quad は階差数列が \ f(n)\ であるから$
\begin{eqnarray*} c_k &=&c_1 + \sum _{n=1}^{k-1}f(n)\\ \\ &=&-\cfrac{a}{2}+ \sum _{n=1}^{k-1}\cfrac{3(1-n)}{(-2)^{n+1}}\\ \\ &=&-\cfrac{a}{2} - \cfrac{3}{2}\sum _{n=1}^{k-1}\big(-\cfrac{1}{2}\big)^n + \cfrac{3}{2} \sum _{n=1}^{k-1} n \big(-\cfrac{1}{2}\big)^n \\ \end{eqnarray*}
$\quad 第2項の和=\cfrac{-\dfrac{1}{2}\big\{1-\big(-\dfrac{1}{2}\big)^{k-1}\big\} }{1+\dfrac{1}{2}}=-\cfrac{1}{3}\big\{1-\big(-\dfrac{1}{2}\big)^{k-1}\big\}$
$\quad 第3項の和を \ \ S_{k-1}\ \ とおくと$
$\qquad S_{k-1}=1 \times \big(-\cfrac{1}{2}\big) + 2 \times \big(-\cfrac{1}{2}\big)^2 + \cdots + (k-2) \times \big(-\cfrac{1}{2}\big)^{k-2} + (k-1) \times \big(-\cfrac{1}{2}\big)^{k-1}$
$\qquad -\cfrac{1}{2}S_{k-1}= \hspace{4em} 1 \times \big(-\cfrac{1}{2}\big)^2 + \cdots + (k-3) \times \big(-\cfrac{1}{2}\big)^{k-2} +(k-2) \times \big(-\cfrac{1}{2}\big)^{k-1} + (k-1) \times \big(-\cfrac{1}{2}\big)^k$
$\quad 辺々引いて$
\begin{eqnarray*} \cfrac{3}{2}S_{k-1} &=&\big(-\cfrac{1}{2}\big) + \big(-\cfrac{1}{2}\big)^2 + \cdots + \big(-\cfrac{1}{2}\big)^{k-1} - (k-1) \big(-\cfrac{1}{2}\big)^k\\ \\ &=&\cfrac{-\dfrac{1}{2}\big\{1-\big(-\dfrac{1}{2}\big)^{k-1}\big\} }{1+\dfrac{1}{2}}- (k-1) \big(-\cfrac{1}{2}\big)^k\\ \\ &=&-\cfrac{1}{3}\big\{1-\big(-\dfrac{1}{2}\big)^{k-1}\big\}- (k-1) \big(-\cfrac{1}{2}\big)^k\\ \end{eqnarray*} $\qquad S_{k-1}=\cfrac{2}{3} \times \Big\{-\cfrac{1}{3}\big\{1-\big(-\dfrac{1}{2}\big)^{k-1}\big\}- (k-1) \big(-\cfrac{1}{2}\big)^k \Big\}$
$\quad よって$
\begin{eqnarray*} c_k &=&-\cfrac{a}{2} + \cfrac{3}{2} \times \cfrac{1}{3}\big\{1-\big(-\dfrac{1}{2}\big)^{k-1}\big\} + \cfrac{3}{2} \times \cfrac{2}{3} \times \Big\{-\cfrac{1}{3}\big\{1-\big(-\dfrac{1}{2}\big)^{k-1}\big\}- (k-1) \big(-\cfrac{1}{2}\big)^k \Big\}\\ \\ &=&-\cfrac{a}{2} + \cfrac{1}{2}\big\{1-\big(-\dfrac{1}{2}\big)^{k-1}\big\} -\cfrac{1}{3}\big\{1-\big(-\dfrac{1}{2}\big)^{k-1}\big\}- (k-1) \big(-\cfrac{1}{2}\big)^k \\ \\ &=&-\cfrac{a}{2} + \cfrac{1}{6} -\cfrac{1}{6}\big(-\dfrac{1}{2}\big)^{k-1}- (k-1) \big(-\cfrac{1}{2}\big)^k \\ \\ &=&\cfrac{1-3a}{6} +\cfrac{1}{3}\big(-\dfrac{1}{2}\big)^k- (k-1) \big(-\cfrac{1}{2}\big)^k \\ \\ &=&\cfrac{1-3a}{6} +\cfrac{4-3k}{3}\big(-\dfrac{1}{2}\big)^k\\ \\ \end{eqnarray*} $\qquad a_k=(-2)^k c_k=(-2)^k \Big\{\cfrac{1-3a}{6} +\cfrac{4-3k}{3}\big(-\dfrac{1}{2}\big)^k \Big\}=\cfrac{1-3a}{6}(-2)^k +\cfrac{4-3k}{3}$
$\quad よって、2\ 以上の自然数 \ k\ 対して \qquad a_k=\cfrac{1-3a}{6}(-2)^k +\cfrac{4-3k}{3}$
メインメニュー に戻る