名古屋大学(理系)2019年前期 問題1
\[ 正の整数nに対し、I_n=\int _0^{\small{\dfrac{\pi}{3}}} \cfrac{d\theta}{\cos ^n \theta} \ \ とする。\]
$(1) \quad I_1を求めよ。必要ならば \ \ \cfrac{1}{\cos \theta}=\cfrac{1}{2}\bigl(\cfrac{\cos \theta}{1+\sin \theta}+\cfrac{\cos \theta}{1-\cos \theta} \bigr)\ \ を使ってよい。$
$(2) \quad n \geqq 3 \ \ のとき、I_n をI_{n-2} とnで表せ。$
$(3) \quad xyz空間においてxy平面内の原点を中心とする半径1の円板をDとする。Dを底面とし、点(0,0,1)を$
$\quad 頂点とする円錐をCとする。Cを平面 \ x=\dfrac{1}{2}\ で2つの部分に切断したとき、小さい方をSとする。$
$\quad z軸に垂直な平面による切り口を考えてSの体積を求めよ。$
$(1)で「等式をつかってよい」は「使わないとできない」と考える。$
$(2)でI_nとI_{n-2}の間の漸化式を導いたのは、(1)のI_1からI_3を求めるためと考える。$
$(3)積分の中にI_3が入ってくればありがたいのだが。$
$\quad でもこれを計算していたら、おそらく時間内に他の問題まで手がまわらないのではないか。$
(1)
\begin{eqnarray*} I_1 &=&\int _0^{\small{\dfrac{\pi}{3}}} \cfrac{d\theta}{\cos \theta}\\ &=&\int _0^{\small{\dfrac{\pi}{3}}} \cfrac{1}{2}\bigl(\cfrac{\cos \theta}{1+\sin \theta}+\cfrac{\cos \theta}{1-\sin \theta} \bigr)d\theta\\ &=&\cfrac{1}{2}\bigl[(\log (1+\sin \theta)-\log (1-\sin \theta ) \bigr]_0^{\small{\dfrac{\pi}{3}}}\\ &=&\cfrac{1}{2}\bigl\{\log (1+\cfrac{\sqrt{3}}{2})-\log (1-\cfrac{\sqrt{3}}{2}) \bigr\}\\ &=&\cfrac{1}{2}\log \cfrac{2+\sqrt{3}}{2-\sqrt{3}}\\ &=&\cfrac{1}{2}\log (2+\sqrt{3})^2\\ &=&\log (2+\sqrt{3})\\ \end{eqnarray*}
$(参考) \quad \cfrac{1}{\cos \theta}=\cfrac{1}{2}\bigl(\cfrac{\cos \theta}{1+\sin \theta}+\cfrac{\cos \theta}{1-\cos \theta} \bigr)\ \ を導いてみましょう。$
\begin{eqnarray*} \cfrac{1}{\cos \theta} &=&\cfrac{\cos \theta}{\cos ^2\theta}\\ &=&\cfrac{\cos \theta}{1-\sin ^2\theta}\\ &=&\cfrac{\cos \theta}{(1+\sin \theta)(1-\sin \theta)}\\ &=&\cfrac{1}{2}\bigl(\cfrac{\cos \theta}{1+\sin \theta}+\cfrac{\cos \theta}{1-\sin \theta} \bigr)\\ \end{eqnarray*} $最後の変形は、部分分数分解を行います。$
(2)
\begin{eqnarray*} I_n &=&\int _0^{\small{\dfrac{\pi}{3}}} \cfrac{d\theta}{\cos ^n \theta}\\ &=&\int _0^{\small{\dfrac{\pi}{3}}} \cfrac{\cos ^2 \theta +\sin ^2 \theta }{\cos ^n \theta}d\theta\\ &=&\int _0^{\small{\dfrac{\pi}{3}}} \cfrac{d\theta}{\cos ^{n-2} \theta} + \int _0^{\small{\dfrac{\pi}{3}}} \cfrac{\sin ^2 \theta }{\cos ^n \theta}d\theta\\ &=&I_{n-2}+ \int _0^{\small{\dfrac{\pi}{3}}} \cfrac{\sin ^2\theta }{\cos ^n \theta} d\theta\\ \end{eqnarray*} $積分項をJ_n とおくと$
\begin{eqnarray*} J_n &=&\int _0^{\small{\dfrac{\pi}{3}}} \cfrac{\sin ^2\theta }{\cos ^n \theta}\\ &=&\int _0^{\small{\dfrac{\pi}{3}}} \cfrac{\sin \theta }{\cos ^n \theta} \times \sin \theta \ d\theta \\ \end{eqnarray*} $\cfrac{\sin \theta }{\cos ^n \theta}\ を積分項として部分積分をおこなう$
\[K=\int \cfrac{\sin \theta }{\cos ^n \theta}d\theta \ \ において\] $\quad \cos \theta =u \ \ とおくと -\sin \theta d\theta=du$
\begin{eqnarray*} K &=&\int \cfrac{-du}{u^n}\\ &=&-\int u^{-n}du\\ &=&\cfrac{1}{n-1}u^{-n+1}\\ &=&\cfrac{1}{n-1}\cfrac{1}{u^{n-1}}\\ &=&\cfrac{1}{n-1}\cfrac{1}{\cos ^{n-1} \theta }\\ \end{eqnarray*} $よって$
\begin{eqnarray*} J_n &=&\bigl[\cfrac{1}{n-1}\cfrac{1}{\cos ^{n-1} \theta }\cdot \sin \theta \bigr]_0^{\small{\dfrac{\pi}{3}}} -\int _0^{\small{\dfrac{\pi}{3}}} \cfrac{1}{n-1}\cfrac{1}{\cos ^{n-1} \theta }\cdot \cos \theta d\theta \\ &=&\cfrac{1}{n-1}\times 2 ^{n-1} \times \cfrac{\sqrt{3}}{2} -\int _0^{\small{\dfrac{\pi}{3}}} \cfrac{1}{n-1}\cfrac{1}{\cos ^{n-2} \theta } d\theta \\ &=&\cfrac{2^{n-2}\sqrt{3}}{n-1}-\cfrac{1}{n-1}I_{n-2}\\ \end{eqnarray*} $したがって$
\begin{eqnarray*} I_n &=&I_{n-2}+J_n\\ \\ &=&I_{n-2}+\cfrac{2^{n-2}\sqrt{3}}{n-1}-\cfrac{1}{n-1}I_{n-2}\\ \\ &=&\cfrac{n-2}{n-1}I_{n-2}+\cfrac{2^{n-2}\sqrt{3}}{n-1}\\ \end{eqnarray*}
(3)
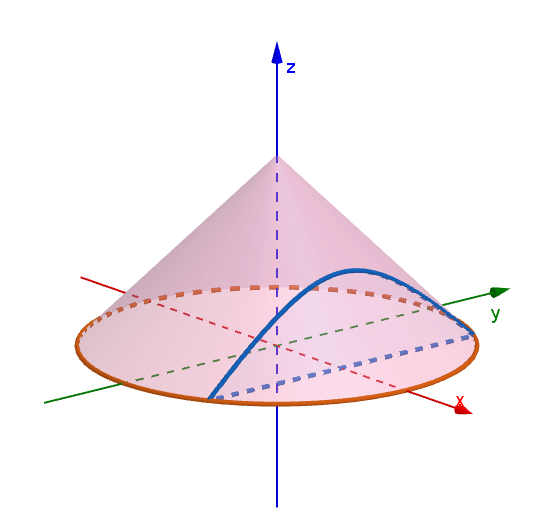
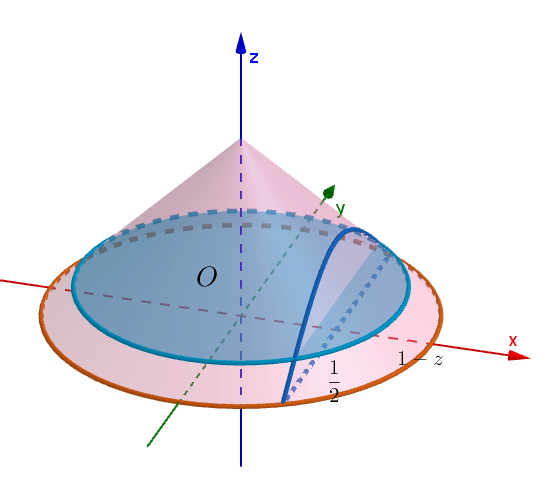
$この円錐Cをz軸に垂直な平面で切った切り口は半径1-zの円で、その方程式は \ \ x^2+y^2=(1-z)^2$
$この円を平面x=\cfrac{1}{2}で切ると断面は、図のような三日月形となる。この面積をTとすると$
\[T=2\int _{\small{\dfrac{1}{2}}}^{1-z} \sqrt{(1-z)^2-x^2}dx\]
$\qquad x=(1-z)\cos \theta \ \ と変換すると$
\[dx=-(1-z)\sin \theta d \theta \qquad
\begin{array}{c|c}
x& \ \small{\dfrac{1}{2}} \rightarrow 1-z\\
\hline
\theta &t \rightarrow 0\ \\
\end{array}
\qquad ただし、(1-z)\cos t=\cfrac{1}{2} \]
\begin{eqnarray*}
T
&=&2\int _t^0 (1-z)\sqrt{1-\cos ^2\theta}\ (-(1-z)\sin \theta d\theta )\\
&=&2\int _0^t (1-z)^2\sin ^2\theta d\theta \\
&=&2(1-z)^2\int _0^t \cfrac{1-\cos 2\theta}{2} d\theta \\
&=&(1-z)^2\bigl[\theta -\cfrac{1}{2}\sin 2\theta \bigr]_0^t \\
&=&(1-z)^2\bigl(t -\cfrac{1}{2}\sin 2t \bigr) \\
\end{eqnarray*}
$よって、Sの体積Vは$
\begin{eqnarray*}
V
&=&\int _0^{\small{\dfrac{1}{2}}} Tdz \\
&=&\int _0^{\small{\dfrac{1}{2}}} (1-z)^2 \bigl(t -\cfrac{1}{2}\sin 2t \bigr)dz \\
\end{eqnarray*}
\[1-z=\cfrac{1}{2\cos t} \ \ より \qquad -dz=\cfrac{1}{2}\cfrac{\sin t}{\cos ^2 t}dt \qquad
\begin{array}{c|c}
z& 0 \rightarrow \small{\dfrac{1}{2}} \\
\hline
t &\small{\dfrac{\pi}{3}} \rightarrow 0\ \\
\end{array}
\]
\begin{eqnarray*}
V
&=&\int _{\small{\dfrac{\pi}{3}}}^0 \cfrac{1}{4\cos ^2 t}\bigl(t -\cfrac{1}{2}\sin 2t \bigr) \bigl(-\cfrac{1}{2}\cfrac{\sin t}{\cos ^2 t}dt \bigr)\\
&=&\cfrac{1}{8}\int _0^{\small{\dfrac{\pi}{3}}} \cfrac{\sin t}{\cos ^4 t}\bigl(t -\cfrac{1}{2}\sin 2t \bigr)dt \\
&=&\cfrac{1}{8}\Bigl(\int _0^{\small{\dfrac{\pi}{3}}} \cfrac{t\sin t}{\cos ^4 t}dt -
\int _0^{\small{\dfrac{\pi}{3}}} \cfrac{\sin t}{\cos ^4 t}\cfrac{\sin 2t}{2}dt \Bigr) \\
\end{eqnarray*}
$この積分の第1項をL_1,第2項をL_2とおく$
(i)$L_1は部分積分法で求める$
\[\int \cfrac{\sin t}{\cos ^4 t}dt=\int (-\cos t)'\cos ^{-4} t dt=\cfrac{1}{3}\cos ^{-3}t=\cfrac{1}{3\cos ^3 t} \ \ だから\]
\begin{eqnarray*}
L_1
&=&\bigl[\cfrac{t}{3\cos ^3 t} \bigr]_0^{\small{\dfrac{\pi}{3}}}
-\int _0^{\small{\dfrac{\pi}{3}}} \cfrac{dt}{3\cos ^3 t}\\
&=&\cfrac{8}{9}\pi -\cfrac{1}{3}\int _0^{\small{\dfrac{\pi}{3}}} \cfrac{dt}{\cos ^3 t}\\
&=&\cfrac{8}{9}\pi -\cfrac{1}{3}I_3\\
\end{eqnarray*}
$ここで、(1)(2)で求めたI_3が使われます。$
(ii)
\begin{eqnarray*}
L_2
&=&\int _0^{\small{\dfrac{\pi}{3}}} \cfrac{\sin t}{\cos ^4 t}\cfrac{\sin 2t}{2}dt\\
&=&\int _0^{\small{\dfrac{\pi}{3}}} \cfrac{\sin t}{\cos ^4 t}\times \sin t \cos tdt\\
&=&\int _0^{\small{\dfrac{\pi}{3}}} \cfrac{\sin ^2t}{\cos ^3 t}dt\\
&=&\int _0^{\small{\dfrac{\pi}{3}}} \cfrac{1-\cos ^2 t}{\cos ^3 t}dt\\
&=&\int _0^{\small{\dfrac{\pi}{3}}} \cfrac{1}{\cos ^3 t}dt-\int _0^{\small{\dfrac{\pi}{3}}} \cfrac{1}{\cos t}dt\\
&=&I_3-I_1\\
\end{eqnarray*}
$まず、(1)(2)よりI_3を求めておきます。$
$I_3=\cfrac{1}{2}I_1+\cfrac{2\sqrt{3}}{2}=\cfrac{1}{2}I_1+\sqrt{3}$
(i)(ii)$より$
\begin{eqnarray*}
V
&=&\cfrac{1}{8}(L_1-L_2)\\
&=&\cfrac{1}{8}\big\{\bigl(\cfrac{8}{9}\pi -\cfrac{1}{3}I_3\bigr)-(I_3-I_1)\bigr\}\\
&=&\cfrac{\pi}{9}-\cfrac{1}{6}I_3+\cfrac{1}{8}I_1\\
&=&\cfrac{\pi}{9}-\cfrac{1}{6}(\cfrac{1}{2}I_1+\sqrt{3})+\cfrac{1}{8}I_1\\
&=&\cfrac{\pi}{9}-\cfrac{\sqrt{3}}{6}+\cfrac{1}{24}I_1\\
&=&\cfrac{\pi}{9}-\cfrac{\sqrt{3}}{6}+\cfrac{1}{24}\log(2+\sqrt{3})\\
\end{eqnarray*}
$これで解けましたが、解答欄のスペースはどの位あったのでしょうか。$
$なお、$x軸に垂直な平面による切り口$を考えてもSの体積を求めることができますので、$
名古屋大学(理系)2019年前期 問題1別解$を参照してください。$
メインメニュー に戻る