名古屋大学(文系)2018年前期 問題3

$を考える。2点P,Qが6個の頂点A,B,C,D,E,Fを以下の$
$規則(a),(b)に従って移動する。$
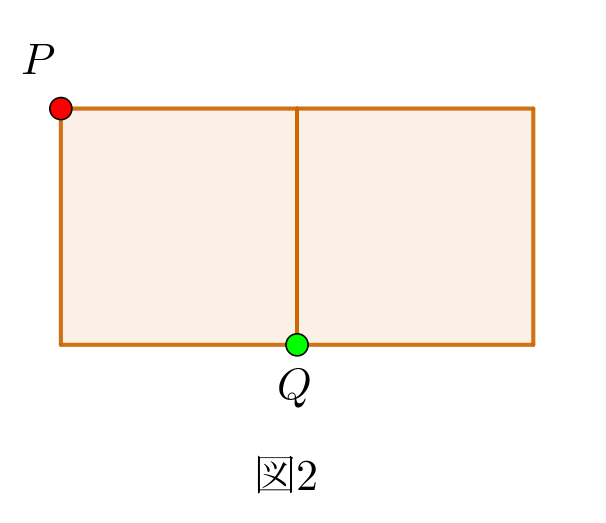
$\quad (a)\ \ 時刻0では図2のように点Pは頂点Aに、点Qは$
$\hspace{2em}頂点Cにいる。$
$\quad (b)\ \ 点P,Qは時刻が1増えるごとに独立に、今いる頂点$
$\hspace{2em}と辺で結ばれている頂点に等確率で移動する。$
$確率をp_nと表す。また時刻nまでに2点P,Qが同時に同じ頂点$
$にいることが一度もなく、かつ時刻nに2点P,Qがともに同じ$
$正方形上にいる確率をa_nと表し、b_n=p_n-a_n と定める。$
$このとき、次の問いに答えよ。$
$(1)\ 時刻1での点P,Qの可能な配置を、図2にならってすべて図示せよ。$
$(2)\ a_1,b_1,a_2,b_2を求めよ。$
$(3)\ a_{n+1},b_{n+1} をa_n,b_nで表せ。$
$(4)\ p_n \leqq \big(\cfrac{3}{4}\big)^n を示せ$
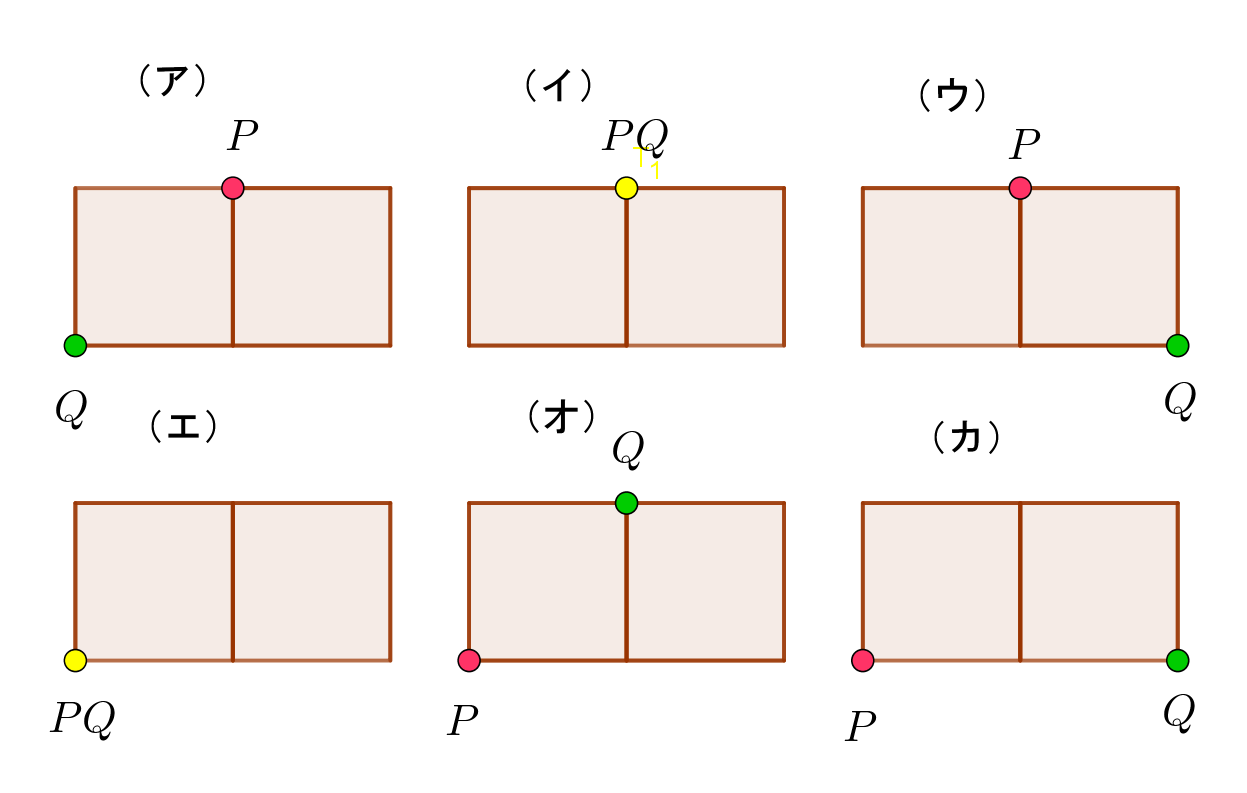
(1)
$右図のとおり、全部で6通りある。$
(2)
$問い(1)から$
$\quad p_1=\cfrac{4}{6}=\cfrac{2}{3}$
$\quad a_1=\cfrac{3}{6}=\cfrac{1}{2}$
$\quad b_1=p_1-a_1=\cfrac{4}{6}-\cfrac{3}{6}=\cfrac{1}{6}$
$次の問いに進む前に、規則(a),(b)を整理しましょう。$
$ある時刻nにおいて、$
(i)$\ \ 2点P,Qが同じ頂点にいることを「消滅」とし、この事象をGとしましょう。$
$\qquad 事象Gが起きたときは、その後の移動はありません。$
(ii)$\ \ 2点P,Qが同じ正方形上にいる事象をHとしましょう。$
$\qquad 事象Hが起こる確率がP(H)=a_n です。$
(iii)$\ \ 2点P,Qが異なる正方形の上の辺、あるいは下辺にいる事象をIとしましょう。$
$\qquad 事象Iが起こる確率がP(I)=b_n です。$
$問い(1)の配置図の$
(i)$\ \ (イ),(エ)は事象Gの根元事象で、この時刻で消滅しました。$
(ii)$\ \ (ア),(ウ),(オ)は事象Hの根元事象ですが、次の時刻での移動は$
$\quad (ア)の状態は、始めの図2でP,Qを交換し、さらに上下を入れ換えたものだから、(ア)からの$
$\qquad 移動も(ア)~(カ)にこの変換を行った6通りとなる。$
$\quad (ウ)の状態は、始めの図2でP,Qを交換し、さらに上下左右を入れ換えたものだから、(ウ)からの$
$\qquad 移動も(ア)~(カ)にこの変換を行った6通りとなる。$
$\quad( オ)の状態は、始めの図2で上下を入れ換えたものだから、(オ)からの移動も(ア)~(カ)に$
$\qquad この変換を行った6通りとなる。$
$\quad したがって(ア),(ウ),(オ)からの移動で、事象G,H,Iの個数は図2からの移動の個数に同じです。$
(iii)$\ \ (カ)は事象Iの根元事象で、次の時刻に移動できるのは次の4通りがあります。$
$\hspace{3em}$
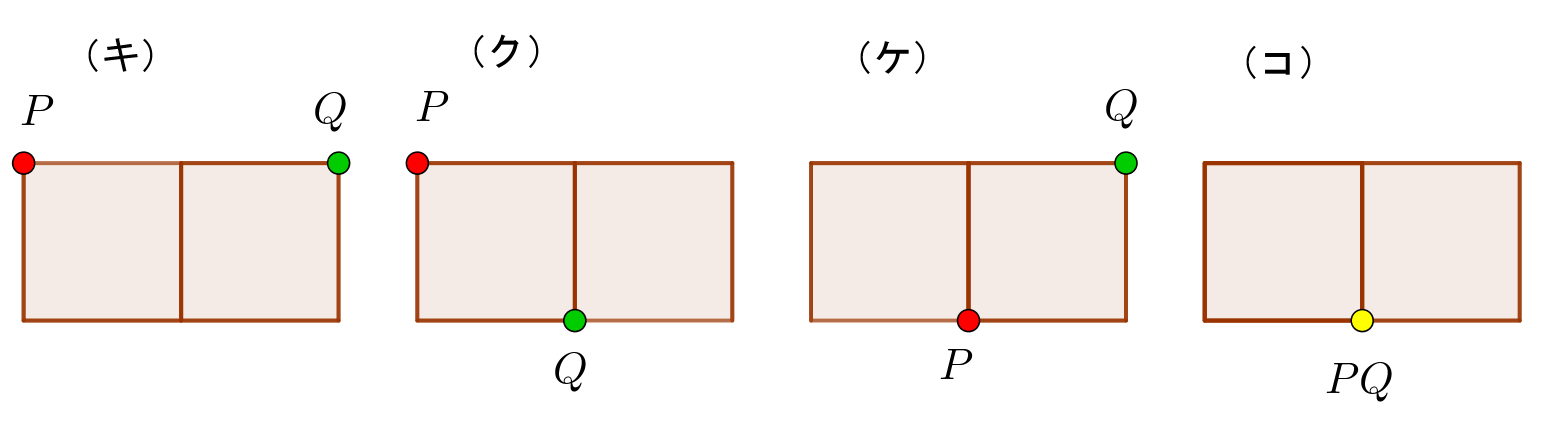
$①\ \ (コ)は事象Gの根元事象で、この時刻で消滅しました。$
$②\ \ (ク),(ケ)は事象Hの根元事象ですが、次の時刻での移動は$
$\quad (ク)の状態は、始めの図2と同じだから、(ク)からの移動は、上の(ア)~(カ)の6通りとなる。$
$\quad (ケ)の状態は、(オ)でP,Qを交換し、さらに上下左右を入れ換えたものだから、(ケ)からの$
$\qquad 移動も(オ)からの移動にこの変換を行った6通りとなる。$
$③\ \ (キ)は事象Iの根元事象で、(カ)で上下を入れ換えたものだから、(キ)からの移動も$
$\qquad (キ)~(コ)の移動にこの変換を行った4通りとなる。$
$すなわち、任意の時刻nでの事象H,Iの各要素の状態から、時刻n+1への移動による$
$事象G,H,Iの要素の個数は$
$\qquad $(i)$\ \ 事象Hについては 2個,3個,1個$
$\qquad $(ii)$\ \ 事象Iについては 1個,2個,1個$
$となる。$
$これらをまとめて樹形図で表すと$
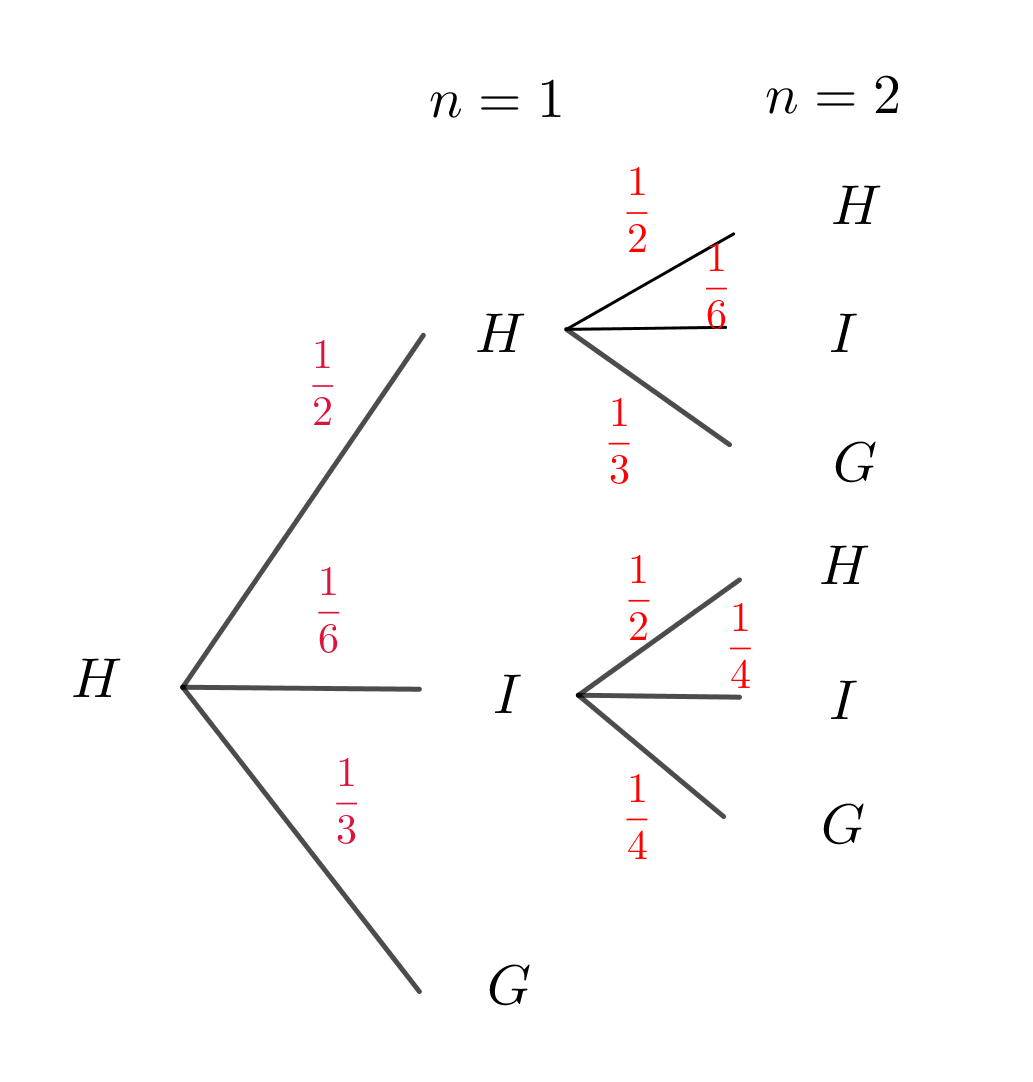
$\hspace{2em}この樹形図から$
$\hspace{3em}a_2=\cfrac{1}{2} \times \cfrac{1}{2} + \cfrac{1}{6} \times \cfrac{1}{2}=\cfrac{1}{3}$
$\hspace{3em}b_2=\cfrac{1}{2} \times \cfrac{1}{6} + \cfrac{1}{6} \times \cfrac{1}{4}=\cfrac{1}{8}$
(3)
$\hspace{3em}$ 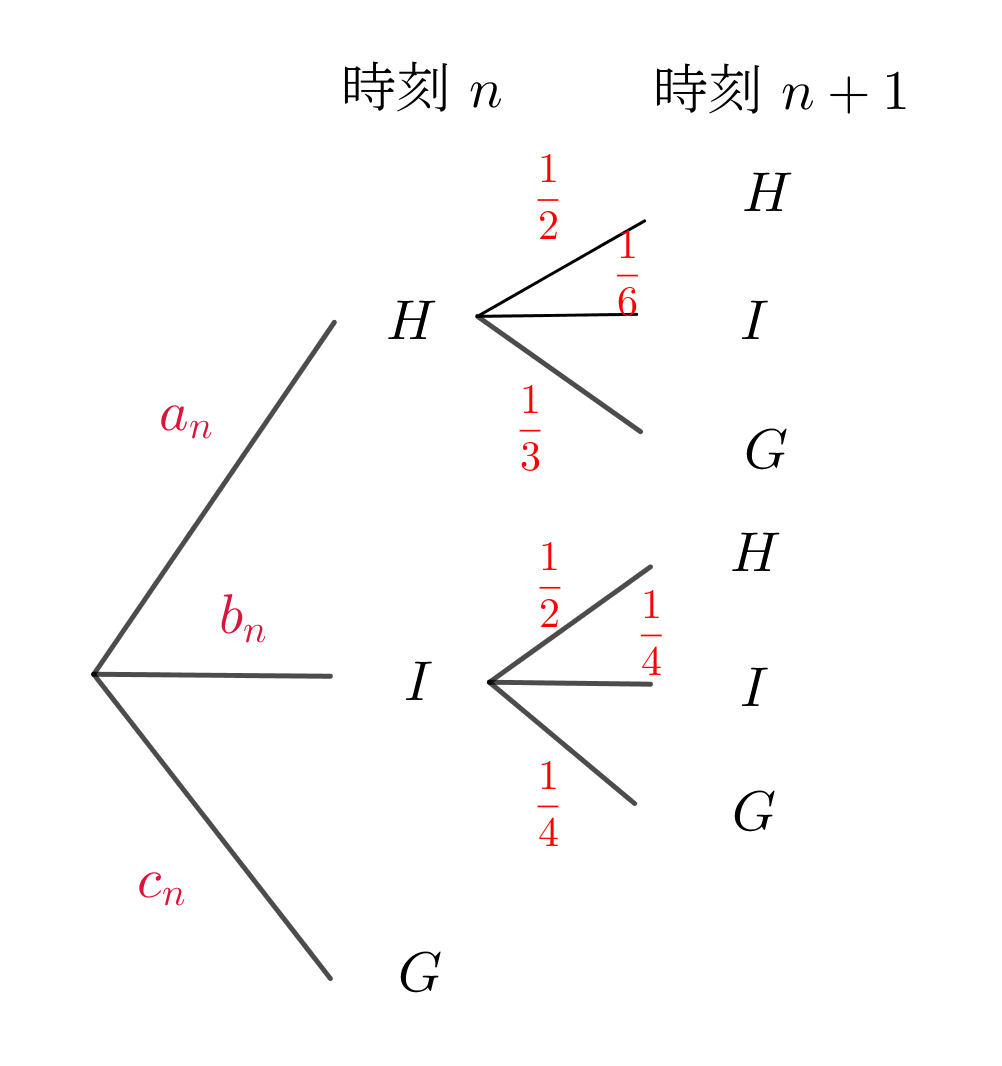
$\hspace{2em}この樹形図から$
$\hspace{3em}a_{n+1}=\cfrac{1}{2}a_n+\cfrac{1}{2}b_n$
$\hspace{3em}b_{n+1}=\cfrac{1}{6}a_n+\cfrac{1}{4}b_n$
(4)
$\qquad p_n=a_n+b_n だから(3)の2式を加えて$
\begin{eqnarray*} p_{n+1}&=&a_{n+1}+b_{n+1}\\ &=&\cfrac{1}{2}a_n + \cfrac{1}{2}b_n + \cfrac{1}{6}a_n + \cfrac{1}{4}b_n\\ &=&\cfrac{2}{3}a_n + \cfrac{3}{4}b_n\\ &=&\cfrac{3}{4}(a_n+b_n)-\cfrac{1}{12}a_n\\ & \leqq & \cfrac{3}{4}p_n\\ \end{eqnarray*} $\qquad \therefore p_n \leqq \cfrac{3}{4}p_{n-1} \leqq \big(\cfrac{3}{4}\big)^2p_{n-2} \leqq \cdots \leqq \big(\cfrac{3}{4} \big)^{n-1}p_1$
$\quad p_1=\cfrac{2}{3} \ \ だから$
$p_n \leqq \cfrac{2}{3}\big(\cfrac{3}{4}\big)^{n-1} \leqq \cfrac{3}{4}\big(\cfrac{3}{4}\big)^{n-1} =\big(\cfrac{3}{4}\big) ^n$
$(注)実際には等号は成りたちません。$
$(別解)$
$数学的帰納法で示します。$
(i)$\ \ n=1 \ \ のとき p_1=\cfrac{2}{3} \leqq \cfrac{3}{4} \ \ で成りたちます。$
(ii)$\ \ n=k \ \ のとき成りたつとすると p_k \leqq \big(\cfrac{3}{4}\big)^n$
$このとき$
\begin{eqnarray*} p_{k+1}&=&a_{k+1}+b_{k+1}\\ &=&\cfrac{2}{3}a_k+\cfrac{3}{4}b_k\\ & \leqq & a_k +b_k\\ &=&p_k\\ & \leqq & \big(\cfrac{3}{4}\big)^k \\ \end{eqnarray*}
$となって n=k+1 \ \ のときも成りたつ。$
$このことから$
$n \rightarrow \infty \ \ のとき p_n \rightarrow 0 \ \ だから$
$0 \leqq a_n \leqq p_n \ \ より a_n \rightarrow 0 $
$0 \leqq b_n \leqq p_n \ \ より b_n \rightarrow 0 $
$これは時間が経つにつれて$
$P,Qが消滅してしまうこと$
$を意味しています。$
$したがってこの問題のポイント$
$は、P,Qが消滅するまでどの位$
$の時間生存できるかということ$
$になります。$
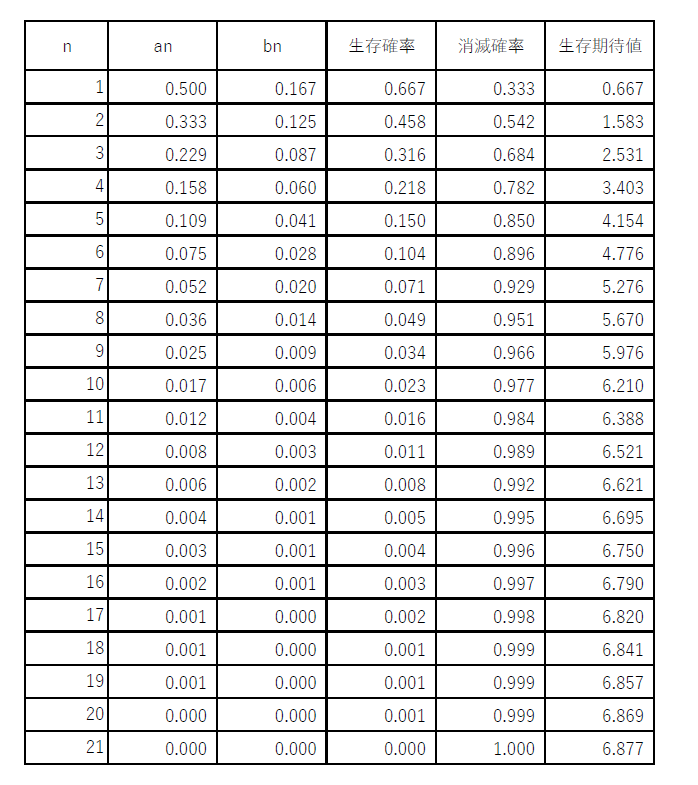
$(3)の漸化式をつかって計算した$
$のが右の表です。$
$n=6で9割方消滅してしまい、$
$n=21で完全消滅(絶滅)して$
$しまうことがわかります。$
$そこで、絶滅するまでの時間の$
$期待値をもとめてみたところ、6.8時間ほどであることがわかりました。$
$入試問題も時間があれば、このように考察できておもしろいですね。$
メインメニュー に戻る