複素数平面上の直線と円
$z=x+yi \ \ とおくと \quad \overline{z}=x-yi\quad より \quad x=\cfrac{z+\overline{z}}{2},\quad y=\cfrac{z-\overline{z}}{2i}=-i\cfrac{z-\overline{z}}{2}$
$(1)\ \ 直線$
$\quad ax+by+c=0 \ \ に代入して$
$\quad a\big(\cfrac{z+\overline{z}}{2}\big)+b\big(-i\cfrac{z-\overline{z}}{2}\big)+c=0$
$\quad \cfrac{1}{2}(a-bi)z+\cfrac{1}{2}(a+bi)\overline{z} +c=0$
$\quad \alpha =\cfrac{1}{2}(a-bi)\quad とおくと \quad \overline{\alpha}=\cfrac{1}{2}(a+bi)\quad だから$
$\quad \alpha \ z+\overline{\alpha}\ \overline{z}+c=0 \quad (cは実数)$
$(2)\ \ 円$
(i)$\ \ x^2+y^2+ax+by+c=0 \quad に代入して$
$\quad z\ \overline{z}+a\big(\cfrac{z+\overline{z}}{2}\big)+b\big(-i\cfrac{z-\overline{z}}{2}\big)+c=0$
$\quad z\ \overline{z}+\cfrac{1}{2}(a-bi)z+\cfrac{1}{2}(a+bi)\overline{z} +c=0$
$\quad \alpha =\cfrac{1}{2}(a-bi)\quad とおくと \quad \overline{\alpha}=\cfrac{1}{2}(a+bi)\quad だから$
$\quad z\ \overline{z}+\alpha z+ \overline{\alpha }\ \overline{z} +c=0$
$ただし (x+\cfrac{a}{2})^2+(y+\cfrac{b}{2})^2=\cfrac{a^2+b^2}{4}-c\quad と平方完成すると$
$\qquad \cfrac{a^2+b^2}{4}-c>0 \quad だから \quad \alpha \ \overline{\alpha}-c>0 \qquad \therefore \ |\alpha|^2> c$
(ii)$\ \ 複素数平面上で、中心\alpha,半径rの円の方程式は$
$\quad |z-\alpha |=r \quad だから$
$\quad |z-\alpha |^2=r^2 $
$\quad (z-\alpha )(\overline{z-\alpha })=r^2$
$\quad (z-\alpha )(\overline{z}-\overline{\alpha })=r^2$
$\quad z\ \overline{z}-\overline{\alpha}\ z- \alpha \ \overline{z}=r^2-|\alpha |^2$
$例 \quad |z+1|=|2\overline{z}-i|\quad をみたす複素数 \ z\ がえがく図形$
$解1$
$z=x+yi\ \ (x,yは実数)\ \ とおくと \quad \overline{z}=x-yi$
$|z+1|^2=|x+1+yi|^2=(x+1)^2+y^2$
$|2\overline{z}-i|^2=|2x-(2y+1)i|^2=4x^2+(2y+1)^2$
$よって (x+1)^2+y^2=4x^2+(2y+1)^2$
$3x^2+3y^2-2x+4y=0$
$(x-\cfrac{1}{3})^2+(y+\cfrac{2}{3})^2=\cfrac{5}{9}$
$よって \ \ z\ は、中心 \ \ \cfrac{1-2i}{3},\quad 半径 \ \ \cfrac{\sqrt{5}}{3} \ \ の円をえがく。$
$解2$
$|z+1|^2=|2\overline{z}-i|^2 \quad より \quad (z+1)(\overline{z}+1)=(2\overline{z}-i)(2z+i)$
$z\overline{z}+z+\overline{z}+1=4z\overline{z}+2i\overline{z}-2iz+1$
$3z\overline{z}-(1+2i)z-(1-2i)\overline{z}=0$
$z\overline{z}-\cfrac{1+2i}{3}z-\cfrac{1-2i}{3}\overline{z}=0$
$(z-\cfrac{1-2i}{3})(\overline{z}-\cfrac{1+2i}{3})=\cfrac{5}{9}$
$|z-\cfrac{1-2i}{3}|^2=\cfrac{5}{9}$
$|z-\cfrac{1-2i}{3}|=\cfrac{\sqrt{5}}{3}$
$よって \ \ z\ は、中心\ \ \cfrac{1-2i}{3}、半径 \ \ \cfrac{\sqrt{5}}{3} \ \ の円をえがく。$
$解3$
$\quad |z+1|=2|\overline{z}-\cfrac{i}{2}|$
$|\overline{z}-\cfrac{i}{2}|=\big|\overline{z+\small{\cfrac{i}{2}}}\big|=|z+\cfrac{i}{2}|\quad だから$
$\quad |z+1|=2|z+\cfrac{i}{2}|$
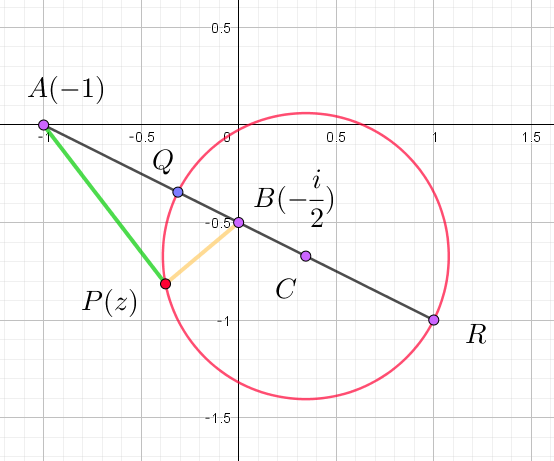
$これは、A(-1),B(-\cfrac{i}{2})からの距離の比が \ 2:1\ であることを$
$示しているので、アポロニウスの円である。$
$内分点 Q:\cfrac{-1+2 \times (-\cfrac{i}{2})}{2+1}=\cfrac{-1-i}{3} \hspace{3em} 外分点 R:\cfrac{(-1)\times (-1)+2 \times (-\cfrac{i}{2})}{2-1}=1-i$
$中点は \cfrac{1}{2}\big(\cfrac{-1-i}{3}+1-i\big)=\cfrac{1-2i}{3} \qquad よって\quad 中心は \ \ C(\cfrac{1-2i}{3})$
$直径はQR=|(1-i)-\cfrac{-1-i}{3}|=|\cfrac{4-2i}{3}|=\cfrac{2\sqrt{5}}{3} \qquad よって \quad 半径は \ \ \cfrac{\sqrt{5}}{3}$
メインメニュー に戻る