MY MATH NOTE

九州大学(理系) 2022年　問題1

$座標空間内の \ 5\ 点 \ O(0,\ 0,\ 0),\ A(1,\ 1,\ 0),\ B(2,\ 1,\ 2),\ P(4,\ 0,\ -1),\ Q(4,\ 0,\ 5)\ を考える。$
$3\ 点 \ O,\ A,\ B\ を通る平面を \ \alpha \ とし、\vec{a}=\vec{OA},\ \ \vec{b}=\vec{OB}\ \ とおく。以下の問いに答えよ。$
$(1)\ \ ベクトル \ \vec{a},\ \vec{b}\ の両方に垂直であり、x\ 成分が正であるような、大きさが \ 1\ のベクトル \ \vec{n}\ を求めよ。$
$(2)\ \ 平面 \ \alpha \ に関して点 \ P\ と対称な点 \ P'\ の座標を求めよ。$
$(3)\ \ 点 \ R\ が平面 \ \alpha \ 上を動くとき、|\vec{PR}|+|\vec{RQ}|\ が最小となるような点 \ R\ の座標を求めよ。$

(1)

　
$\quad \vec{n}=(l,m,n) \quad とおく$
$\qquad \vec{a} \perp \vec{n} \quad より \quad \vec{a}\cdot \vec{n}=l+m=0 \hspace{6em}①$
$\qquad \vec{b} \perp \vec{n} \quad より \quad \vec{b}\cdot \vec{n}=2l+m+n=0 \hspace{4em}②$
$\qquad |\vec{n}|=1 \quad より \quad l^2+m^2+n^2=1 \hspace{5em}\ \ ③$

$\quad ①より \quad m=-l$
$\quad ②に代入して \quad 2l-l+2n=0 \qquad l=-2n \quad よって \quad m=2n$

$\quad これらを③に代入して \quad (-2n)^2+(2n)^2+n^2=1 $

$\qquad 9n^2=1 \qquad l > 0 \quad より \quad n < 0 \qquad \therefore \ \ n=-\cfrac{1}{3}$

$\qquad よって \quad l=\cfrac{2}{3},\quad m=-\cfrac{2}{3} \qquad \therefore \ \ \vec{n}=(\cfrac{2}{3},\ -\cfrac{2}{3},\ -\cfrac{1}{3})$

$(別解)$

$\quad 平面 \ \ \alpha \ を \ \ ax+by+cz=d \quad とおくと$
$\qquad 点 \ O\ を通るから \hspace{5em} d=0$
$\qquad 点 \ A(1,\ 1,\ 0)\ を通るから \quad a+b=0 \qquad b=-a \hspace{5em}④$
$\qquad 点 \ B(2,\ 1,\ 2)\ を通るから \quad 2a+b+2c=0$
$\qquad ④を代入して \quad 2a-a+2c=0 \qquad a=-2c \quad よって \quad b=2c$

$\quad したがって \ \ \alpha \ \ は \quad -2cx+2cy+cz=0 \quad すなわち \quad 2x-2y-z=0$

$\qquad \alpha \ \ の法線ベクトルは \ (2,\ -2,\ -1) \ で、この大きさは \ \ \sqrt{2^2+(-2)^2+(-1)^2}=3 \quad だから$

$\quad 大きさ \ 1\ の法線ベクトルは \ \ \vec{n}=(\cfrac{2}{3},\ -\cfrac{2}{3},\ -\cfrac{1}{3})$

(2)

　
$\quad \vec{PP'} /\!/ \vec{n} \quad より \quad \vec{PP'}=k\vec{n}\ \ (kは実数で \ \ k \ne 0)\ とおけるから$

$\quad \vec{OP'}-\vec{OP}=k\vec{n}$

$\quad \vec{OP'}=\vec{OP}+k\vec{n}=(4,\ 0,\ -1)+ k(\cfrac{2}{3},\ -\cfrac{2}{3},\ -\cfrac{1}{3})=(4+\cfrac{2}{3}k,\ -\cfrac{2}{3}k,\ -1-\cfrac{1}{3}k)$

$\quad 2\ 点 \ P,\ P'の中点を \ M\ とすると$

$\quad \vec{OM}=\cfrac{1}{2}(\vec{OP}+\vec{OP'})=(4+\cfrac{k}{3},\ -\cfrac{k}{3},\ -1-\cfrac{k}{6})$

$\quad M\ は \ \alpha \ 上にあるから \quad 2(4+\cfrac{k}{3})-2 \times (-\cfrac{k}{3})-(-1-\cfrac{k}{6})=0 \qquad \therefore \ \ k=-6$

$\quad よって \quad \vec{OP'}=(4+\cfrac{2}{3} \times (-6),\ -\cfrac{2}{3} \times (-6),\ -1-\cfrac{1}{3} \times (-6))=(0,\ 4,\ 1) \qquad P'(0,\ 4,\ 1)$

(3)

　
$\quad f(x,\ y,\ z)=2x-2y-z \quad とおくと$

$\quad f(4,\ 0,\ -1)=9,\quad f(4,\ 0,\ 5)=3 \quad だから \ 2\ 点 \ P,\ Q\ は$
$\quad 平面 \ \alpha \ の同じ正の領域にある。$

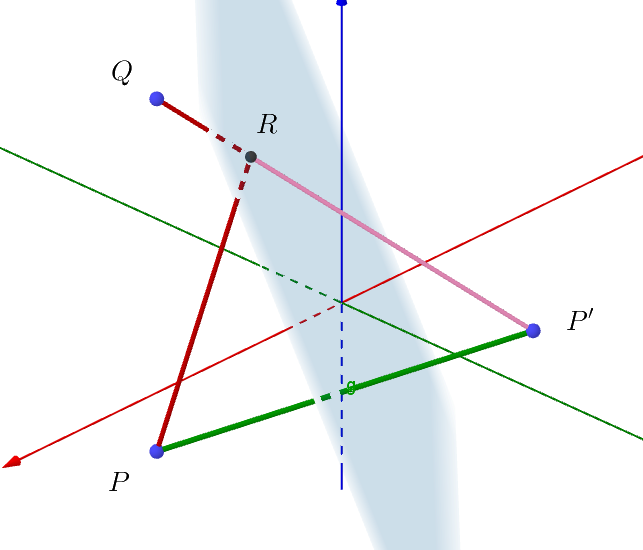
$\quad 点 \ P\ の平面 \ \alpha \ に関する対称な点 \ P'\ は(2)より \ \ P'(0,4,1)$

$\quad |\vec{PR}|+|\vec{RQ}|=PR+RQ =P'R+RQ \ \ が最小となるのは$
$\quad 3\ 点 \ P',\ R,\ Q \ が一直線上にあるときだから \quad P'R:RQ=(1-t):t \quad とおくと$

$\quad \vec{OR}=t\vec{OP'}+(1-t)\vec{OQ}=t(0,\ 4,\ 1)+ (1-t)(4,\ 0,\ 5)=(4-4t,\ 4t,\ 5-4t)$

$\quad 点 \ R\ は \ \ \alpha \ \ 上にあるから \quad 2(4-4t)-2 \times 4t-(5-4t)=0 \qquad t=\cfrac{1}{4}$

$\quad よって \quad \vec{OR}=(3,\ 1,\ 4) \qquad \therefore \ \ R(3,\ 1,\ 4)$


$(研究)$

$(1)\ \ の\ \vec{a},\ \vec{b}\ の両方に垂直なベクトルは外積を用いて$
\[\vec{a} \times \vec{b}= \left| \begin{array}{rr} \vec{i} & \vec{j} & \vec{k}\\ 1 & 1 & 0\\ 2 & 1 & 2\\ \end{array} \right| =2\vec{i} -2\vec{j} -\vec{k} =(2,-2,-1) \] $と簡単に求められます。$

ページの先頭へ↑