九州大学(理系) 2021年 問題2
$\theta \ \ を \ \ 0 < \theta < \cfrac{\pi}{4}\ \ をみたす定数とし、x\ の \ 2\ 次方程式 \quad x^2-(4\cos \theta )x + \cfrac{1}{\tan \theta }=0 \qquad \cdots \ \ (*)$
$を考える。以下の問いに答えよ。$
$(1)\ \ 2\ 次方程式 \ (*)\ が実数解をもたないような \ \theta\ の値の範囲を求めよ。$
$(2)\ \ \theta \ が(1)で求めた範囲にあるとし、(*)\ の2つの虚数解を \ \alpha,\ \beta \ とする。ただし、\alpha \ の虚部は \ \beta \ の虚部$
$\qquad より大きいとする。複素数平面上の \ 3\ 点 \ A(\alpha),\ B(\beta),\ O(0)\ を通る円の中心を \ C(\gamma)\ とするとき、$
$\qquad \theta \ を用いて \ \gamma \ を表せ。$
$(3)\ \ 点 \ O,\ A,\ C\ を(2)のように定めるとき、三角形 \ OAC\ が直角三角形になるような \ \theta \ に対する \ \tan \theta \ の値$
$\qquad を求めよ。$
$(解説)$
$(1)\ \ 判別式で \ \ 1+\tan ^2 \theta =\cfrac{1}{\cos ^2 \theta}\ \ をつかって \ \ \tan \theta \ の \ 2\ 次不等式に直すと \ \theta \ の値の範囲を求めるのは困難です。$
$(2)\ \ A(\alpha)\ と \ B(\beta) \ は実軸に関して対称で、円の中心は弦 \ AB\ の垂直二等分線上にあることから \ \gamma \ は実数となります。$
$(3)\ \ \triangle \ AOC \ が直角三角形になるのは、\angle C=90°\ のときだけです。$
(1)
$x^2-(4\cos \theta )x + \cfrac{1}{\tan \theta }=0 \ \ が実数解をもたない条件は$
$\quad \cfrac{D}{4}=(2\cos \theta)^2- \cfrac{1}{\tan \theta } < 0 \qquad 0 < \theta < \cfrac{\pi}{4} \quad より \quad \tan \theta > 0 \quad だから 両辺に \ \ \tan \theta \ \ をかけて$
$\quad 4\cos ^2\theta \tan \theta -1 <0 \qquad 4\sin \theta \cos \theta -1 <0$
$\quad 2\sin 2\theta -1 < 0 \qquad 0 < 2\theta < \cfrac{\pi}{2} \quad より \quad 0 < \sin 2\theta < \cfrac{1}{2}$
$\quad 0 < 2\theta < \cfrac{\pi}{6} \qquad \therefore \ \ 0 < \theta < \cfrac{\pi}{12}$
(2)
$x^2-(4\cos \theta )x + \cfrac{1}{\tan \theta }=0 \quad の虚数解は$
$\quad x=2\cos \theta \pm \sqrt{4\cos ^2\theta -\cfrac{1}{\tan \theta }}=2\cos \theta \pm i\sqrt{\cfrac{1}{\tan \theta }-4\cos ^2\theta }$
$\alpha \ の虚部は \ \beta \ の虚部より大きいから$
$\quad \alpha =2\cos \theta + i\sqrt{\cfrac{1}{\tan \theta }-4\cos ^2\theta },\qquad \beta =2\cos \theta - i\sqrt{\cfrac{1}{\tan \theta }-4\cos ^2\theta }$
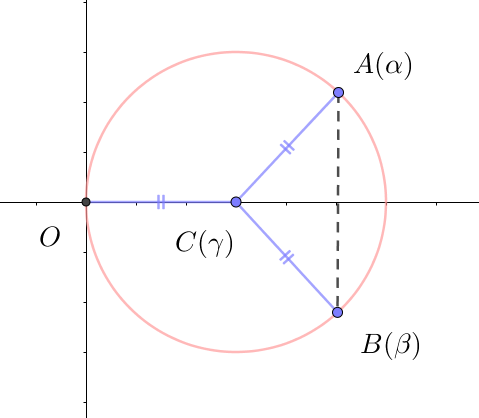
$円は原点 \ O\ を通り、Re(\alpha)=Re(\beta) =2\cos \theta > 0 \quad で \quad A(\alpha) \ と \ B(\beta)\ は$
$実軸に関して対称だから、円の中心 \ C(\gamma)\ は実軸上の正の部分にある。$
$OC=AC \quad より \quad |\gamma|=|\gamma - \alpha|$
$\gamma =\Big|\gamma -2\cos \theta - i\sqrt{\cfrac{1}{\tan \theta }-4\cos ^2\theta }\Big|$
$\gamma ^2=(\gamma -2\cos \theta)^2+\big(\cfrac{1}{\tan \theta }-4\cos ^2\theta \big)$
$\gamma ^2=\gamma ^2 -4\gamma \cos \theta +4cos ^2\theta + \cfrac{1}{\tan \theta }-4\cos ^2\theta $
$4\gamma \cos \theta =\cfrac{1}{\tan \theta } \qquad \therefore \ \ \gamma=\cfrac{1}{\tan \theta } \times \cfrac{1}{4\cos \theta}=\cfrac{1}{4\sin \theta}$
(3)
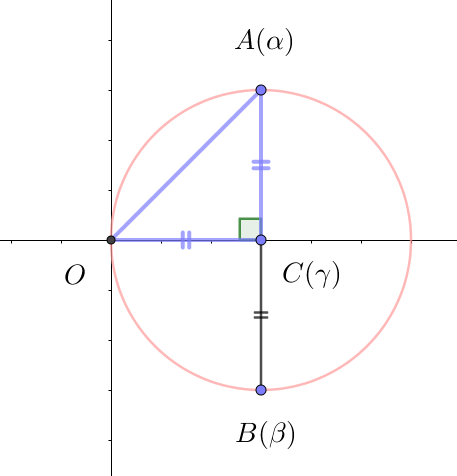
$\triangle OAC\ が直角三角形になるのは、右図のように \ \angle C=90°\ の場合しかない。$
$このとき、Re(\alpha)=\gamma \quad だから \quad 2\cos \theta=\cfrac{1}{4\sin \theta}$
$2\sin \theta \cos \theta=\cfrac{1}{4} \qquad \sin 2\theta=\cfrac{1}{4}$
$ところで、t=\tan \theta \quad とおくと$
$\quad \sin 2\theta =2\sin \theta \cos \theta=\cfrac{2\sin \theta \cos \theta}{\sin ^2\theta + \cos ^2\theta}=\cfrac{2\tan \theta}{\tan ^2\theta +1}=\cfrac{2t}{1+t^2}$
$よって \quad \cfrac{2t}{1+t^2}=\cfrac{1}{4} \quad より \quad t^2-8t+1=0 \qquad t=4 \pm \sqrt{15}$
$0 < \theta < \cfrac{\pi}{4} \quad だから \quad 0 < \tan \theta <1 \quad よって \quad t=\tan \theta=4-\sqrt{15}$
メインメニュー に戻る