球面三角形の面積
1 球面三角形の面積
$(1)\ \ 月形の面積$
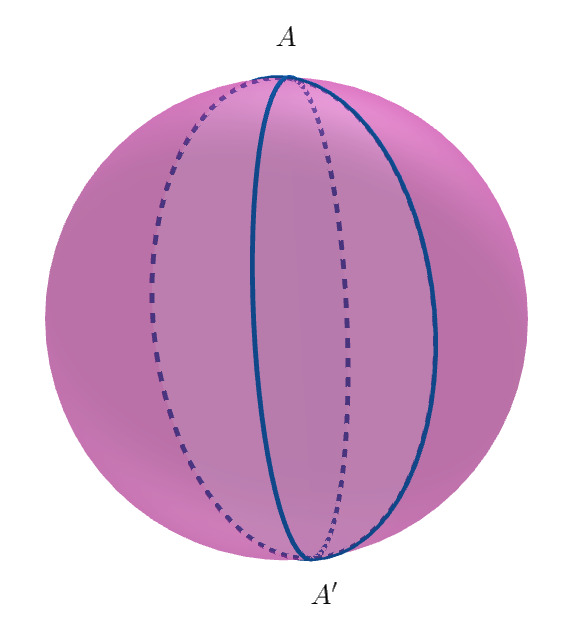
$右図のように、球面上の2点Aと、中心Oにおける対称点A'を通る2つの大円で$
$囲まれた図形を月形といいます。$
$この月形の面積Sは、\angle A\ (今後単にAとかきます)\ に比例するから$
$球の半径をRとすると$
$\qquad S=\cfrac{A}{2\pi} \times 4\pi R^2=2R^2A$
$(2)\ \ 球面三角形ABCの面積$
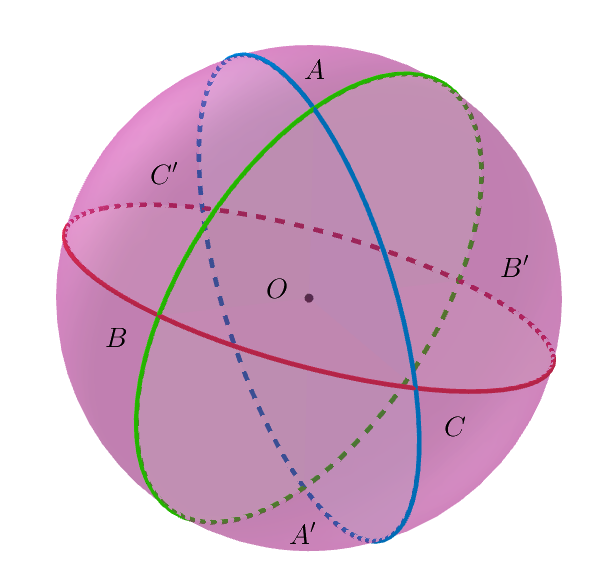
$右図のように、球面三角形ABCの各頂点の中心Oにおける対称点を$
$A',B',C'とする。$
$\triangle ABCと\triangle A'BC の和は大円ABA'と大円ACA'で囲まれた月形となるので、$
$その面積は(1)より$
$\qquad \triangle ABC + \triangle A'BC=2R^2A$
$同様にして$
$\qquad \triangle BCA + \triangle B'CA=2R^2B$
$\qquad \triangle CAB + \triangle C'AB=2R^2C$
$\triangle ABC=\triangle BCA=\triangle CAB \ \ に注意してこれらを加えると$
$\qquad 3\triangle ABC+ \triangle A'BC + \triangle B'CA + \triangle C'AB=2R^2(A+B+C)$
$\triangle C'AB と \triangle CA'B' は中心Oについて対称だから$
$\qquad \triangle C'AB=\triangle CA'B' $
$よって$
$\qquad \triangle ABC+ \triangle A'BC + \triangle B'CA + \triangle C'AB=\triangle ABC+ \triangle A'BC + \triangle B'CA + \triangle CA'B'$
$右辺は図では、緑の右半球となるからその面積は\ \ 2\pi R^2$
$したがって$
$\qquad 2\triangle ABC+ 2\pi R^2=2R^2(A+B+C)$
$\qquad \therefore \triangle ABC =R^2(A+B+C-\pi)$
$\qquad 球面三角形ABCの面積$
$\hspace{3em} \triangle ABC =R^2(A+B+C-\pi)$
2 球面三角形の内角の和
$球面三角形の面積 \ \ \triangle ABC =R^2(A+B+C-\pi) \ \ は正であることから$
$\qquad \pi < A+B+C$
$となります。$
$平面三角形では A+B+C=\pi \ \ ですからこれは驚くべき内容です。$
$また、A <\pi,\ B <\pi,\ C <\pi \ \ だからこれらを加えて$
$\qquad A+B+C < 3\pi$
$したがって$
$\qquad \pi < A+B+C < 3\pi $
$\qquad 球面三角形ABCの内角の和$
$\hspace{3em} \pi < A+B+C < 3\pi$
3 球面幾何
$(1)球面三角形の内角の和は2直角より大きい。$
$(2)球面三角形では、大円を辺と見なしたが、これを直線とすると有限となる。$
$(3)2つの大円は北半球と南半球で必ず交わるので、直線 \ l \ 外の点を通り、l \ に平行な直線は1本もない。$
$このように、球面上で展開される幾何は、平面上のユークリッド幾何とはだいぶ様子を異にするもので$
$リーマンの非ユークリッド幾何のモデルです。$
メインメニュー に戻る