京都大学(理系) 2025年　問題5


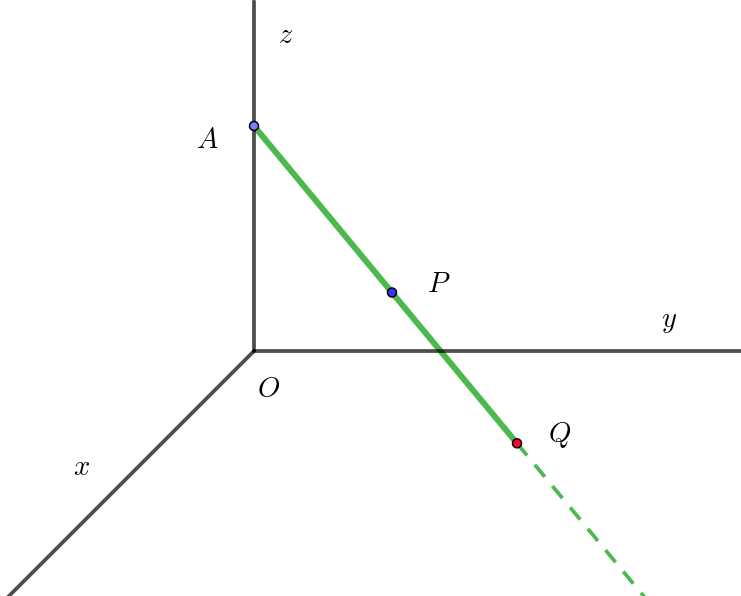
$\theta \ は実数とする。xyz\ 空間の \ 2\ 点A(0,\ 0,\dfrac{\sqrt{2}}{4}),\ \ P(\cos \theta,\ \sin \theta,\ \dfrac{1}{2}\cos \theta)\ \ を通る直線 \ AP\ がxy\ 平面と$
$交わるとき、その交点を \ Q\ とする。\theta \ が \ \ -\dfrac{\pi}{4} < \theta < \dfrac{\pi}{4}\ \ の範囲を動くときの点 \ Q\ の軌跡を求め、$
$その軌跡を \ xy\ 平面上に図示せよ。$

　

$\dfrac{1}{2}\cos \theta=\dfrac{\sqrt{2}}{4}\ \ となるのは \quad \cos \theta=\dfrac{\sqrt{2}}{2}\ \ のとき$

$すなわち \quad \theta=\pm \dfrac{\pi}{4}\ \ だから \quad -\dfrac{\pi}{4} < \theta < \dfrac{\pi}{4}\ \ の範囲では\ \ AP /\!/ xy 平面 $

$になることはない。したがって AP\ は必ず \ xy\ 平面と交わる。$

$Q(x,\ y,\ 0)\ \ とおく。$

$3\ 点A,\ P,\ Q\ は一直線上にあるから \quad \vec{AQ}=t\vec{AP}\ \ (t\ は実数)\ \ とおける。$

$\vec{OQ}-\vec{OA}=t(\vec{OP}-\vec{OA})$

$(x,\ y,\ 0)-(0,\ 0,\ \dfrac{\sqrt{2}}{4})=t\{(\cos \theta,\ \sin \theta, \ \dfrac{1}{2}\cos \theta)-(0,\ 0,\ \dfrac{\sqrt{2}}{4})\}$

$(x,\ y,\ -\dfrac{\sqrt{2}}{4})=t(\cos \theta,\ \sin \theta, \ \dfrac{1}{2}\cos \theta -\dfrac{\sqrt{2}}{4})$

\[ \hspace{1em} \left\{ \begin{array}{l} x= t\cos \theta \hspace{10.5em}(1)\\ y=t\sin \theta \hspace{11em}(2)\\ -\dfrac{\sqrt{2}}{4}=t(\dfrac{1}{2}\cos \theta -\dfrac{\sqrt{2}}{4}) \hspace{4.5em}(3)\\ \end{array} \right. \]
$(3)より \quad -\sqrt{2}=t(2\cos \theta -\sqrt{2})$

$ -\dfrac{\pi}{4} < \theta < \dfrac{\pi}{4}\ \ だから \quad \cos \theta \ne \dfrac{\sqrt{2}}{2}$

$t=-\dfrac{\sqrt{2}}{2\cos \theta -\sqrt{2}}=\dfrac{1}{1-\sqrt{2}\cos \theta }$

$(1),\ (2)に代入して$

\[ \hspace{1em} \left\{ \begin{array}{l} x=\dfrac{\cos \theta}{1-\sqrt{2}\cos \theta } \hspace{5em}(4)\\ y=\dfrac{\sin \theta}{1-\sqrt{2}\cos \theta } \hspace{5em}(5)\\ \end{array} \right. \]
$(4)より \quad x(1-\sqrt{2}\cos \theta)=\cos \theta$

$(\sqrt{2}x +1)\cos \theta=x$

$ここで\ \ \sqrt{2}x+1 =0 \ \ ならば \quad x=-\dfrac{1}{\sqrt{2}} \quad このとき右辺は \ \ x=0\ \ だから不合理$

$よって \quad \sqrt{2}x +1 \ne 0\ \ だから \quad \cos \theta =\dfrac{x}{\sqrt{2}x +1} \hspace{9em}(6)\\ $

$(5)に代入して$

$\sin \theta =(1-\sqrt{2}\cos \theta)y=\big(1-\sqrt{2} \times \dfrac{x}{\sqrt{2}x +1} \big)y=\dfrac{y}{\sqrt{2}x+1} \hspace{5em}(7)$

$(6),(7) より$

$\cos ^2 \theta + \sin ^2\theta=\big(\dfrac{x}{\sqrt{2}x +1}\big)^2+\big(\dfrac{y}{\sqrt{2}x+1}\big)^2=1$

$x^2+y^2=(\sqrt{2}x+1)^2$

$x^2+2\sqrt{2}x-y^2=-1$

$(x+\sqrt{2})^2-y^2=1 \quad これは双曲線である。$

$ただし \ \ -\dfrac{\pi}{4} < \theta < \dfrac{\pi}{4}\ \ より \quad \dfrac{1}{\sqrt{2}} < \cos \theta \leqq 1$

$(6)に代入して \quad \dfrac{1}{\sqrt{2}} < \dfrac{x}{\sqrt{2}x +1}\leqq 1$

(i)$\ \ \dfrac{1}{\sqrt{2}}　< \dfrac{x}{\sqrt{2}x +1} \quad を解くと$

$\quad \dfrac{x}{\sqrt{2}x +1} - \dfrac{1}{\sqrt{2}}>0$

$\quad \dfrac{\sqrt{2}x-(\sqrt{2}x+1)}{\sqrt{2}x +1} >0$

$\quad \dfrac{-1}{\sqrt{2}x +1} >0$

$\quad \sqrt{2}x +1 <0$

$\quad x < -\dfrac{1}{\sqrt{2}}$

　

(ii)$\ \ \dfrac{x}{\sqrt{2}x +1}\leqq 1 \quad を解くと$

$\quad 1-\dfrac{x}{\sqrt{2}x +1} \geqq 0$

$\quad \dfrac{(\sqrt{2}-1)x+1}{\sqrt{2}x +1} \geqq 0$

$\quad (\sqrt{2}x +1)(\sqrt{2}-1)x+1) \geqq 0$

$\quad (\sqrt{2}x +1)(x + \sqrt{2}+1) \geqq 0$

$\quad x \leqq -(\sqrt{2}+1) , \quad x > -\dfrac{1}{\sqrt{2}}$

(i),(ii)$ \ \ より \quad x \leqq -(\sqrt{2}+1) $

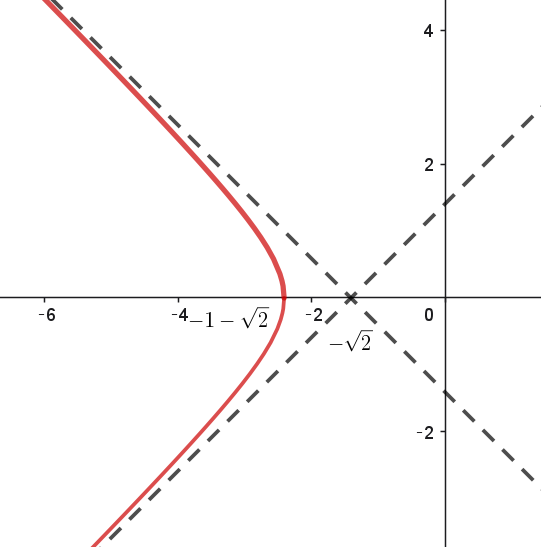
$点 \ Q\ の軌跡は右図のとおり$


ページの先頭へ↑




メインメニュー　に戻る