京都大学(理系) 2025年　問題3


$e\ は自然対数の底とする。x > \dfrac{1}{\sqrt{e}} \ \ において定義された次の関数 \ f(x),\ \ g(x)\ \ を考える。$
$\qquad f(x)=x^2\log x , \qquad g(x)=x^2\log x -\dfrac{1}{1+2\log x}$
$実数 \ t\ は \ \ t > \dfrac{1}{\sqrt{e}}\ \ を満たすとする。曲線 \ y=f(x)\ 上の点(t,\ f(t))\ \ における接線に垂直で、点(t,\ g(t))\ \ を通る$
$直線を \ \ell_1 \ とする。直線 \ \ell_1 \ が \ x\ 軸と交わる点の \ x\ 座標を \ p(t)\ とする。t\ が \ \ \dfrac{1}{\sqrt{e}} < t \leqq e \ \ の範囲を動くとき、$
$p(t)\ の取りうる値の範囲を求めよ。$


$f(x)=x^2\log x \quad より$

$f'(x)=2x\log x+x=x(1+2\log x)$

$x > \dfrac{1}{\sqrt{e}} \ \ だから \quad 1+2\log x > 1+2\log \dfrac{1}{\sqrt{e}}=1-2 \times \dfrac{1}{2}=0$

$よって \quad f'(x) >0 $

$f(\dfrac{1}{\sqrt{e}})=\dfrac{1}{e}\log \dfrac{1}{\sqrt{e}}=-\dfrac{1}{2e}$

$f''(x)=(1+2\log x) +2 > 0 $

$よって \ \ f(x)\ は下に凸な単調増加関数$

　

$g(x)=x^2\log x -\dfrac{1}{1+2\log x} \quad より$

$g'(x)=x(1+2\log x)+\dfrac{2}{x(1+\log x)^2} > 0$

$よって \ \ g(x)\ は単調増加関数$

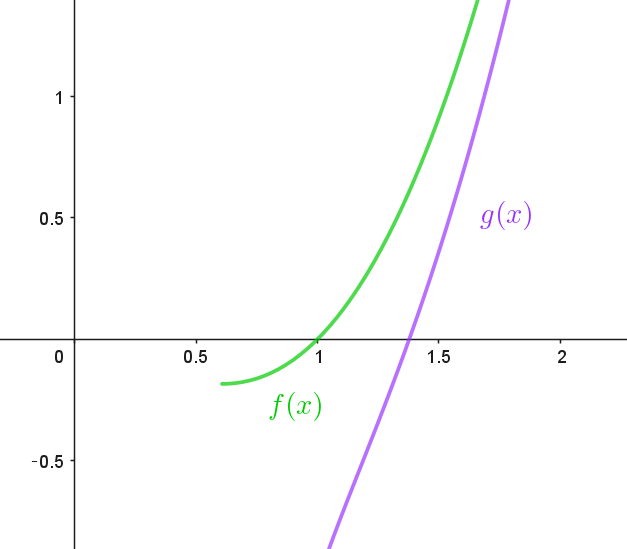
$1+2\log x > 0 \quad だから \quad f(x) > g(x)$

$f(x)\ と \ g(x)\ のグラフは右図のとおり$

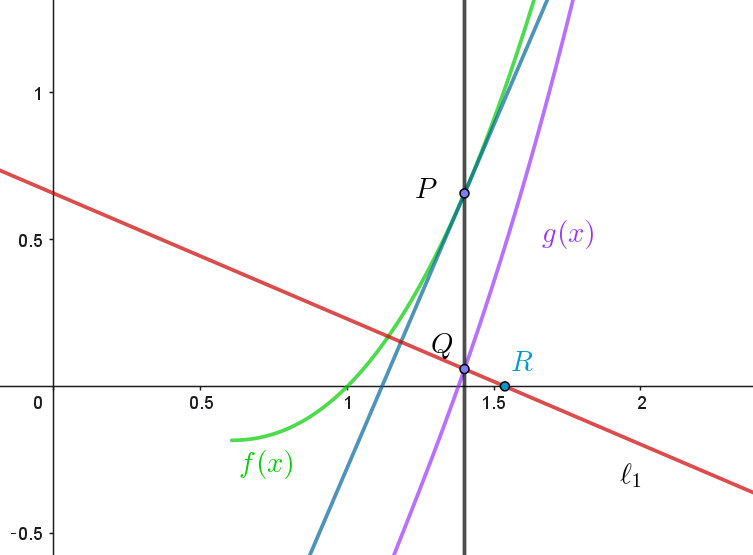
$直線 \ell_1 \ \ は$
\begin{eqnarray*} y &=&-\dfrac{1}{t(1+2\log t)}(x-t)+t^2\log t -\dfrac{1}{1+2\log t}\\ \\ &=&-\dfrac{1}{t(1+2\log t)}x+t^2\log t \\ \end{eqnarray*}

　

$\ell_1 \ \ が \ x\ 軸と交わる点の \ x\ 座標は$

$-\dfrac{1}{t(1+2\log t)}x+t^2\log t =0 \quad を解いて$

$x=t^3\log t(1+2\log t)$

$よって \quad p(t)=t^3\big(\log t+2(\log t)^2\big)$

\begin{eqnarray*} p'(t) &=&3t^2\big(\log t+2(\log t)^2\big)+t^3\big(\dfrac{1}{t}+\dfrac{4\log t}{t}\big)\\ \\ &=&3t^2\big(\log t+2(\log t)^2\big)+t^2(1+4\log t)\\ \\ &=&t^2\big(1+7\log t +6(\log t)^2 \big)\\ \\ &=&t^2(1+6\log t )(1+\log t )\\ \end{eqnarray*} $\dfrac{1}{\sqrt{e}} < t \leqq e \ \ より \quad -\dfrac{1}{2} < \log t \leqq 1 \quad だから \quad 1+\log t >0$

$p'(t)=0 \ \ より \quad \log t=-\dfrac{1}{6} \qquad \therefore \ \ t=\dfrac{1}{\sqrt[6]{e}}$

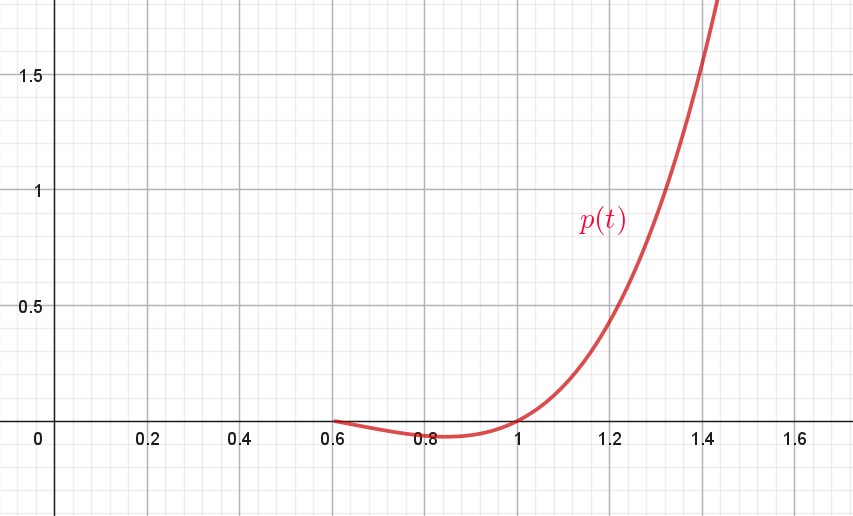
$増減表$
\[ \begin{array}{c||c|c|c|c|c} t& \dfrac{1}{\sqrt{e}} & \cdots & \dfrac{1}{\sqrt[6]{e}} & \cdots & e\\ \hline p'(t)& & - & 0 & + & \\ \hline p(t) & & \searrow & 極小 & \nearrow & \\ \end{array} \]

　

$t=\dfrac{1}{\sqrt[6]{e}}\ で \ p(t)\ は極小かつ最小となり、最小値は$

$p(\dfrac{1}{\sqrt[6]{e}})=\dfrac{1}{\sqrt{e}} \big(-\dfrac{1}{6}+2(-\dfrac{1}{6})^2\big)=-\dfrac{1}{9\sqrt{e}}$

$p(\dfrac{1}{\sqrt{e}})=\dfrac{1}{e\sqrt{e}} \big(-\dfrac{1}{2}+2(-\dfrac{1}{2})^2 \big)=0$

$p(e)=e^3(1+2)=3e^3$

$よって \ p(t)\ の取りうる値の範囲は \quad -\dfrac{1}{9\sqrt{e}} \leqq p(t) \leqq 3e^3$


ページの先頭へ↑




メインメニュー　に戻る