京都大学(理系) 2025年　問題2


$正の整数 \ x,\ y,\ z\ を用いて \ \ N=9z^2=x^6+y^4 \ \ と表される正の整数 \ N\ の最小値を求めよ。$


$すべての正の整数\ m,\ n\ を \ 9\ で割った余りをそれぞれ \ \ k,\ \ell\ \ とすると$

$ x^3=9m+k,\quad y^2=9n+\ell \ \ (k,\ l=0,\ \pm 1,\ \pm 2,\ \pm 3,\ \pm 4)\ \ とおける。$

$x^6=(9m+k)^2=9^2m^2+2\cdot 9km +k^2=9(9m^2+2km)+k^2$

$y^4=(9n+\ell)^2=9^2n^2+2\cdot 9\ell n +\ell ^2=9(9n^2+2\ell n)+\ell ^2$

$x^6+y^4 =9(9m^2+2km+ 9n^2+2\ell n)+k^2+\ell ^2 $

$9z^2=x^6+y^4 \quad より \quad x^6+y^4 \ \ は \ 9\ の倍数だから$

$k^2+ \ell ^2 \ \ は \ 9\ の倍数$

　

$右は \ \ k^2+\ell ^2 \ \ を求めた表で、これが \ 9\ の倍数になるのは$

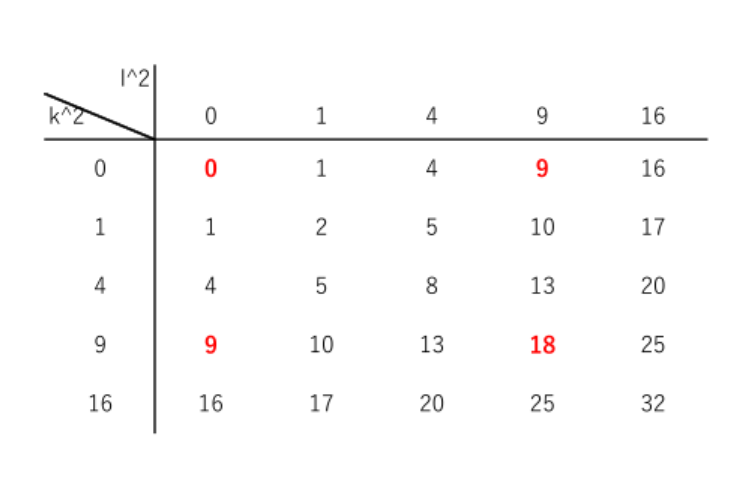
$(k^2,\ \ell ^2)=(0,\ 0),\ \ (0,\ 9),\ \ (9,\ 0),\ \ (9,\ 9)$

$すべての正の整数を \ 9\ で割った余りで類別(分類)すると$

$(9m)^3=9m',\quad (9m \pm 1)^3=9m'\pm 1,\quad (9m \pm 2)^3=9m'\mp1$

$(9m \pm 3)^3=9m', \quad (9m \pm 4)^3=9m'\pm1　だから$

$k^2=9 \quad すなわち \quad k=\pm 3 \ \ の場合$

$x^3=9m \pm 3 \ \ をみたす正の整数 \ x\ はない。$

$同様に$

$(9n)^2=9n',\quad (9n \pm 1)^2=9n'+ 1,\quad (9n \pm 2)^2=9n' +4$

$(9n \pm 3)^2=9n', \quad (9n \pm 4)^2=9n' -2　だから$

$\ell^2=9 \quad すなわち \quad \ell =\pm 3 \ \ の場合$

$y^2=9m \pm 3 \ \ をみたす正の整数 \ y\ はない。$

$したがって \quad (k^2,\ \ell ^2)=(0,\ 0)\ \ のみであるから$

$x^3=9m,\quad y^2=9n \quad このとき \quad 9z^2=(9m)^2+(9n)^2$

$z^2=9(m^2+n^2)$

$左辺は平方数だから \ \ m^2+n^2 \ \ も平方数である。$

$p^2=m^2+n^2 \ \ とおくと \ \ (m,\ n,\ p)\ \ はピタゴラス数であるから、p\ が最小となるのは$

$明らかに \quad (m,\ n,\ p)=(3,\ 4,\ 5)$

$よって \quad x^3=9 \times 3=27,\quad y^2=9 \times 4=36,\quad z^2=9 \times 5^2=225$

$N \ の最小値は \quad N=9z^2=9 \times 225=2025$


$(感想)$

$2025\ 年度の入試問題ということで、「2025」をうまくはめ込んだ問題です。$

$というより、むしろ \ 2025\ を初めから意識して作った問題でしょうか。$


ページの先頭へ↑




メインメニュー　に戻る