MY MATH NOTE

京都大学(理系) 2021年　問題2

$曲線 \ y=\cfrac{1}{2}(x^2+1)\ 上の点 \ P\ における接線は \ x\ 軸と交わるとし、その交点を \ Q\ とおく。線分 \ PQ\ の長さを$
$L\ とするとき、L\ が取りうる値の最小値を求めよ。$

　
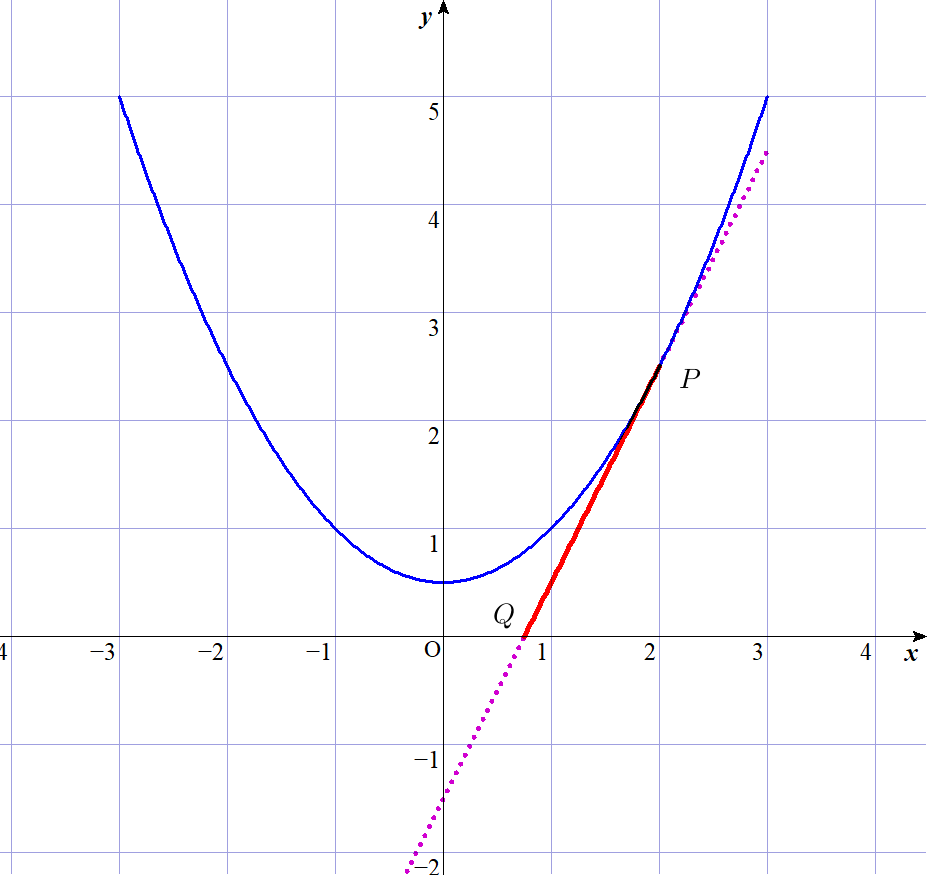
$P(t,\ \cfrac{1}{2}(t^2+1))\ \ とおく。$

$t=0\ のときは接線は \ x\ 軸と交わらない。$

$グラフは \ y\ 軸について対称だから \ t > 0\ と考えてよい。$

$点 \ P\ における接線は \ \ y'=x \ \ より$

$\quad y=t(x-t)+\cfrac{1}{2}(t^2+1) \quad すなわち \quad 　y=tx-\cfrac{1}{2}t^2+\cfrac{1}{2}$

$x\ 軸との交点は \ \ y=0 \ \ とおいて$

$\quad x=\cfrac{t^2-1}{2t} \quad よって \quad Q(\cfrac{t^2-1}{2t},\ 0)$

\begin{eqnarray*} L^2 &=&\big(t-\cfrac{t^2-1}{2t}\big)^2+\big(\cfrac{1}{2}(t^2+1)\big)^2\\ &=&\cfrac{(t^2+1)^2}{4t^2}+\cfrac{(t^2+1)^2}{4}\\ &=&\cfrac{1}{4}(t^2+1)^2\big(\cfrac{1}{t^2}+1\big)\\ &=&\cfrac{(t^2+1)^3}{4t^2}\\ \end{eqnarray*} $\quad f(t)=\cfrac{(t^2+1)^3}{t^2} \quad とおくと$

\begin{eqnarray*} f'(t) &=&\cfrac{3(t^2+1)^2 \times 2t \times t^2-(t^2+1)^3 \times 2t}{t^4}\\ \\ &=&\cfrac{2(t^2+1)^2\{ 3t^2-(t^2+1)\}}{t^3}\\ \\ &=&\cfrac{2(t^2+1)^2\{ 2t^2-1)\}}{t^3}\\ \end{eqnarray*}

　
$\quad f'(t)=0 \quad より \quad t=\cfrac{1}{\sqrt{2}}$

\[ \begin{array}{c||c|c|c|c} \hline t & 0 & \cdots & \cfrac{1}{\sqrt{2}} & \cdots \\ \hline f'(t) & & - & 0 & + \\ \hline f(t) & & \searrow & 極小 & \nearrow \\ \end{array} \]
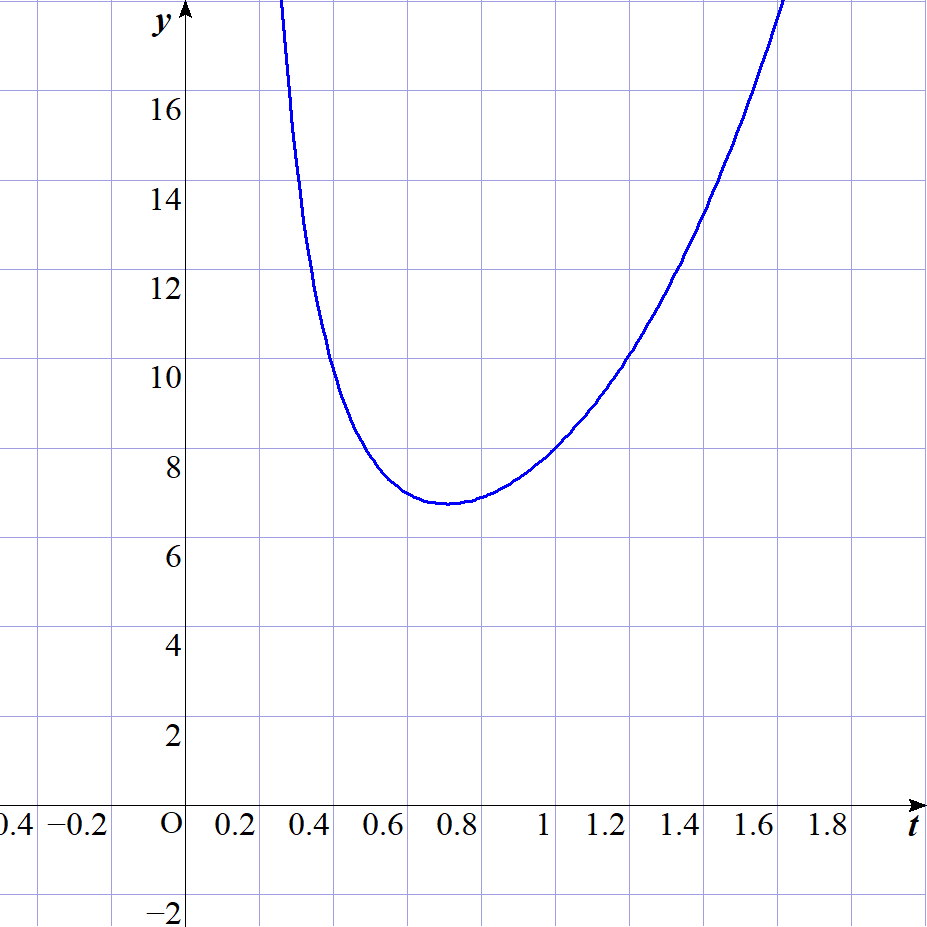
$右図は \ y=f(t)\ のグラフです。$

$\quad t=\cfrac{1}{\sqrt{2}}\ \ で極小かつ最小、最小値は \quad f(\cfrac{1}{\sqrt{2}})=(\cfrac{1}{2}+1)^3 \times 2=\cfrac{27}{4}$

$\quad よって \quad L\ の最小値は \quad t=\pm \cfrac{1}{\sqrt{2}}\ \ のとき \ \ \sqrt{\cfrac{1}{4} \times \cfrac{27}{4}}=\cfrac{3\sqrt{3}}{4}$

ページの先頭へ↑