神戸大学(理系) 2021年 問題5
$座標平面上を運動する点 \ P(x,\ y)\ の時刻 \ t\ における座標が \ \ x=\cfrac{4+5\cos t}{5+4\cos t},\quad y=\cfrac{3\sin t}{5+4\cos t}\ \ であるとき、$
$以下の問に答えよ。$
$\qquad (1)\ \ 点 \ P\ と原点 \ O\ との距離を求めよ。$
$\qquad (2)\ \ 点 \ P\ の時刻 \ t\ における速度 \ \ \vec{v}=\big(\cfrac{dx}{dt},\ \cfrac{dy}{dt}\big)\ \ と速さ \ \ |\vec{v}|\ を求めよ。$
\[(3)\ \ 定積分 \ \ \int _0^{\pi}\cfrac{dt}{5+4\cos t} \ \ を求めよ。\]
$(解説)$
$(1)\ \ ごく普通に \ OP^2\ を計算します。$
$(2)\ \ 速度はベクトル、速さは速度の大きさで、スカラーです。$
$(3)\ \ ここで定積分の問題は唐突な感じがしますが、(2)が使われます。$
(1)
\begin{eqnarray*} OP^2 &=&\big(\cfrac{4+5\cos t}{5+4\cos t}\big)^2+\big(\cfrac{3\sin t}{5+4\cos t}\big)^2\\ \\ &=&\cfrac{16+40\cos t+25\cos ^2t + 9\sin ^2t}{(5+4\cos t)^2}\\ \\ &=&\cfrac{16+40\cos t+16\cos ^2t + 9(\cos ^2t +\sin ^2t)}{(5+4\cos t)^2}\\ \\ &=&\cfrac{25+40\cos t+16\cos ^2t}{(5+4\cos t)^2}\\ \\ &=&\cfrac{(5+4\cos t)^2}{(5+4\cos t)^2}\\ \\ &=&1\\ \end{eqnarray*} $\qquad \therefore \ \ OP=1$
(2)
\begin{eqnarray*} \cfrac{dx}{dt} &=&\cfrac{-5\sin t(5+4\cos t)-(4+5\cos t)(-4\sin t)}{(5+4\cos t)^2}\\ \\ &=&\cfrac{-25\sin t -20\sin t \cos t +16\sin t +20\sin t \cos t }{(5+4\cos t)^2}\\ \\ &=&\cfrac{-9\sin t }{(5+4\cos t)^2}\\ \end{eqnarray*}
\begin{eqnarray*} \cfrac{dy}{dt} &=&\cfrac{3\cos t(5+4\cos t)-3\sin t(-4\sin t)}{(5+4\cos t)^2}\\ \\ &=&\cfrac{15\cos t +12\cos ^2t +12\sin ^2 t }{(5+4\cos t)^2}\\ \\ &=&\cfrac{12+ 15\cos t }{(5+4\cos t)^2}\\ \end{eqnarray*} $\qquad \therefore \ \ \vec{v}=\big(\cfrac{-9\sin t }{(5+4\cos t)^2},\ \ \cfrac{12+ 15\cos t }{(5+4\cos t)^2}\big)$
\begin{eqnarray*} |\vec{v}|^2 &=&\cfrac{(-9\sin t)^2}{(5+4\cos t)^4}+ \cfrac{(12+ 15\cos t)^2 }{(5+4\cos t)^4}\\ \\ &=&\cfrac{9\{9\sin ^2 t+(4+ 5\cos t)^2\} }{(5+4\cos t)^4}\\ \\ &=&\cfrac{9(9\sin ^2 t+16+ 40\cos t +25\cos ^2 t)}{(5+4\cos t)^4}\\ \\ &=&\cfrac{9(25+ 40\cos t +16\cos ^2 t)}{(5+4\cos t)^4}\\ \\ &=&\cfrac{9(5+ 4\cos t)^2 }{(5+4\cos t)^4}\\ \\ &=&\cfrac{9}{(5+4\cos t)^2}\\ \end{eqnarray*} $\qquad \therefore \ \ |\vec{v}|=\cfrac{3}{5+4\cos t}$
(3)
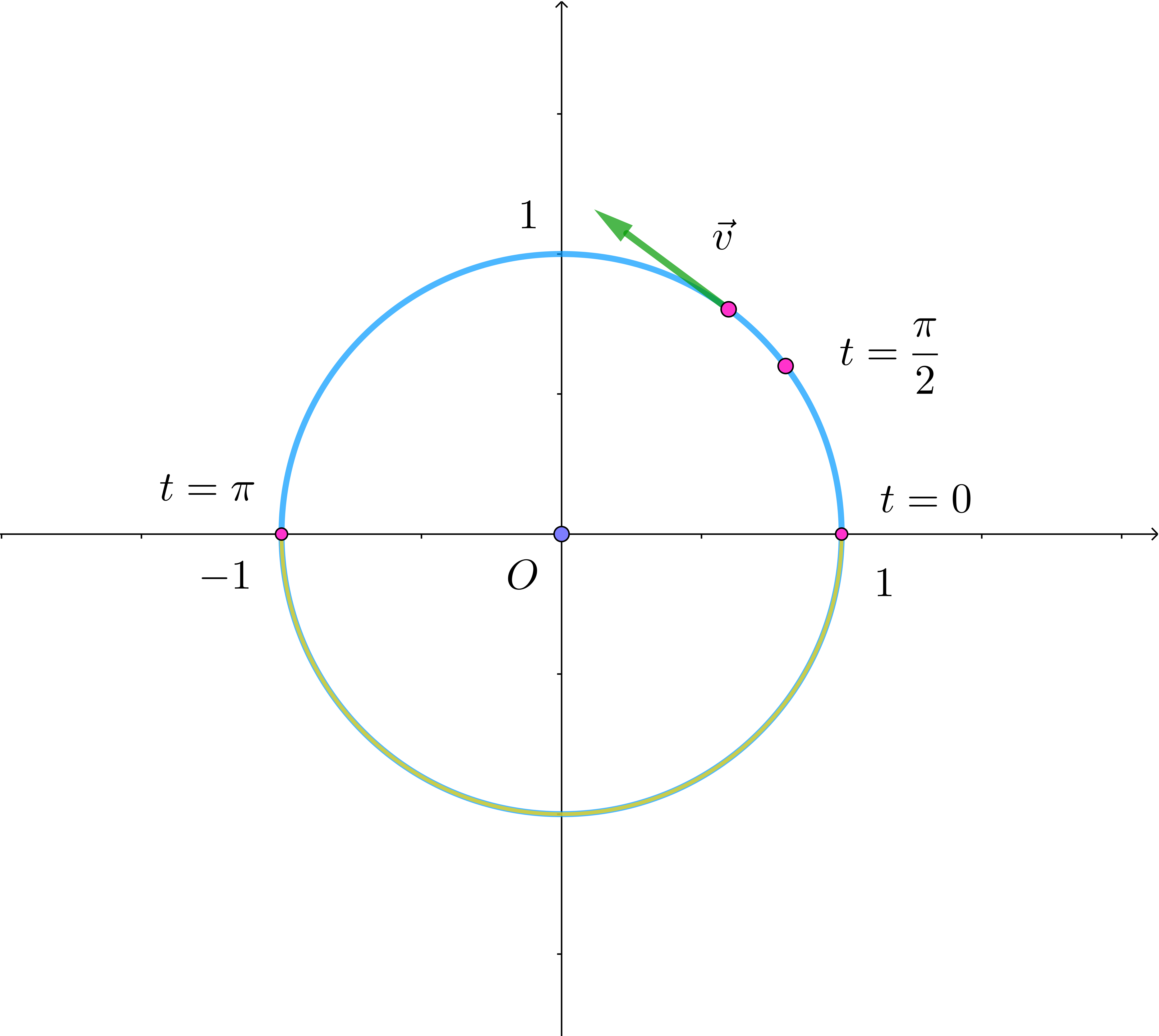
\begin{eqnarray*} I &=&\int _0^{\pi}\cfrac{dt}{5+4\cos t}\\ \\ &=&\int _0^{\pi}\cfrac{|\vec{v}|}{3}dt\\ \\ &=&\cfrac{1}{3}\int _0^{\pi}|\vec{v}|dt\\ \end{eqnarray*} \[\int _0^{\pi}|\vec{v}|dt \ \ は \ \ 0 \leqq t \leqq \pi\ \ の間に点 \ P\ が動いた距離 \ L\ である。\] $\hspace{3em} t=0 \ \ のとき \quad x=1,\ y=0 \qquad t=\pi \ \ のとき \quad x=-1,\ y=0$
$\quad 点 \ P\ は半円周を動くから \quad L=\cfrac{1}{2} \times 2\pi \times 1=\pi$
$よって I=\cfrac{1}{3}L=\cfrac{\pi}{3}$
$(別解)$
$この定積分をダイレクトに求めてみます。$
\[I=\int _0^{\pi}\cfrac{dt}{5+4\cos t} \quad で \quad \tan \cfrac{t}{2}=u \quad とおくと\] $\qquad (この変数変換(置換)は教科書には出てきませんが、参考書にはあると思います。)$
$\hspace{3em} 1+\tan ^2\cfrac{t}{2}=\cfrac{1}{\cos ^2\cfrac{t}{2}}\quad より \quad \cos ^2\cfrac{t}{2}=\cfrac{1}{1+u^2} \quad よって \quad \cos t=2\cos ^2\cfrac{t}{2}-1=\cfrac{2}{1+u^2}-1=\cfrac{1-u^2}{1+u^2}$
$\hspace{3em} \tan \cfrac{t}{2}=u \quad を微分して \quad \cfrac{dt}{2\cos ^2\cfrac{t}{2}}=du \qquad dt=2\cos ^2\cfrac{t}{2}du=\cfrac{2}{1+u^2}du $
\[ \quad \begin{array}{c|c} t & \ 0\ \ \rightarrow \pi \quad \\ \hline u & \ 0\ \ \rightarrow \infty \\ \end{array} \]
\begin{eqnarray*} I &=&\int _0^{\infty}\cfrac{\dfrac{2}{1+u^2}du}{5+\dfrac{4(1-u^2)}{1+u^2}}\\ \\ &=&\int _0^{\infty}\cfrac{2}{5(1+u^2)+4(1-u^2)}du\\ \\ &=&\int _0^{\infty}\cfrac{2}{9+u^2}du\\ \end{eqnarray*} \[さらに \quad u=3\tan \theta \quad とおくと \quad du=\cfrac{3}{\cos ^2\theta}d\theta \qquad \begin{array}{c|c} u & \ 0\ \ \rightarrow \infty \quad \\ \hline \theta & 0\ \ \rightarrow \cfrac{\pi}{2} \\ \end{array} \] \begin{eqnarray*} I &=&\int _0^{\small{\cfrac{\pi}{2}}}\cfrac{\dfrac{6}{\cos ^2 \theta}d\theta }{9+9\tan ^2\theta}\\ &=&\cfrac{2}{3}\int _0^{\small{\cfrac{\pi}{2}}}\cfrac{d\theta}{(1+\tan ^2\theta)\cos ^2\theta}\\ &=&\cfrac{2}{3}\int _0^{\small{\cfrac{\pi}{2}}}d\theta\\ &=&\cfrac{2}{3} \times \cfrac{\pi}{2}\\ &=&\cfrac{\pi}{3} \end{eqnarray*}
メインメニュー に戻る