神戸大学(理系) 2021年 問題3
$\vec{0}\ \ でない \ 2\ つのベクトル \ \ \vec{a},\ \vec{b}\ が垂直であるとする。\vec{a}+\vec{b}\ と \ \vec{a}+3\vec{b}\ \ のなす角を \ \theta \ \ (0 \leqq \theta \leqq \pi) \ \ とする。$
$以下の問に答えよ。$
$(1)\ \ |\vec{a}|=x,\ \ |\vec{b}|=y \ \ とするとき、\sin ^2\theta \ \ を \ x,\ y\ を用いて表せ。$
$(2)\ \ \theta \ \ の最大値を求めよ。$
$(解説)$
$(1)\ \ \vec{a}+\vec{b}\ と \ \vec{a}+3\vec{b}\ \ の内積を \ 2\ 通りで表現します。$
$(2)\ \ (1)より、\sin ^2 \theta \ \ は \ x,\ y\ の分数関数となりますが、分子を定数にして、分母に相加・相乗平均の$
$\qquad 不等式をつかいます。$
(1)
$\vec{a} \perp \vec{b} \quad より \quad \vec{a} \cdot \vec{b}=0 \quad だから$
$\quad |\vec{a}+\vec{b}|^2=|\vec{a}|^2 + 2\vec{a}\cdot \vec{b} +|\vec{b}|^2=x^2+ y^2$
$\quad |\vec{a}+3\vec{b}|^2=|\vec{a}|^2 + 6\vec{a}\cdot \vec{b} +9|\vec{b}|^2=x^2+ 9y^2$
$\quad (\vec{a}+\vec{b})\cdot (\vec{a}+3\vec{b})=|\vec{a}|+4\vec{a}\cdot \vec{b} +3|\vec{b}|=x^2+3y^2$
$また$
$(\vec{a}+\vec{b})\cdot (\vec{a}+3\vec{b})=|\vec{a}+\vec{b}| |\vec{a}+3\vec{b}| \cos \theta \quad だから$
$\qquad \cos \theta =\cfrac{(\vec{a}+\vec{b})\cdot (\vec{a}+3\vec{b})}{|\vec{a}+\vec{b}| |\vec{a}+3\vec{b}|}=\cfrac{x^2+3y^2}{\sqrt{x^2+y^2}\sqrt{x^2+9y^2}}$
\begin{eqnarray*} \sin ^2 \theta &=&1-\cos ^2 \theta\\ \\ &=&1-\cfrac{(x^2+3y^2)^2}{(x^2+y^2)(x^2+9y^2)}\\ \\ &=&\cfrac{(x^2+y^2)(x^2+9y^2)-(x^2+3y^2)^2}{(x^2+y^2)(x^2+9y^2)}\\ \\ &=&\cfrac{4x^2 y^2 }{(x^2+y^2)(x^2+9y^2)}\\ \end{eqnarray*}
(2)
$分母・分子を \ y^4\ \ (\ne 0)\ \ で割って$
$\quad \sin ^2 \theta=\cfrac{\dfrac{4x^2}{y^2}}{(\dfrac{x^2}{y^2}+1)(\dfrac{x^2}{y^2}+9)} \qquad \cfrac{x^2}{y^2}=t \quad とおくと \quad t > 0$
$\quad \sin ^2 \theta=\cfrac{4t}{(t+1)(t+9)}=\cfrac{4}{(1+\dfrac{1}{t})(t+9)}=\cfrac{4}{10+t+\dfrac{9}{t}}$
$相加・相乗平均の不等式より \quad 分母 \geqq 10+2\sqrt{t \times \cfrac{9}{t}}=16$
$\qquad ただし 等号は \quad t=\cfrac{9}{t} \quad のときで、これより \quad t=3$
$よって \sin ^2 \theta \leqq \cfrac{4}{16}=\cfrac{1}{4}$
$また、(1)の \quad \cos \theta =\cfrac{(\vec{a}+\vec{b})\cdot (\vec{a}+3\vec{b})}{|\vec{a}+\vec{b}| |\vec{a}+3\vec{b}|}=\cfrac{x^2+3y^2}{\sqrt{x^2+y^2}\sqrt{x^2+9y^2}} \quad より \quad \cos \theta > 0 $
$\quad 0 \leqq \theta \leqq \pi \quad だから \quad 0 \leqq \theta < \cfrac{\pi}{2} \qquad \sin \theta \geqq 0 \quad だから \quad 0 \leqq \sin \theta \leqq \cfrac{1}{2}$
$また、この区間で、\sin \theta \ \ は単調増加だから \quad \sin \theta =\cfrac{1}{2} \quad のとき \ \ \theta \ \ は最大で 最大値は \quad \theta =\cfrac{\pi}{6}$
$(別解) \quad 微分法による方法$
$\quad \sin ^2 \theta=f(t)=\cfrac{4t}{(t+1)(t+9)} \quad (t > 0) \quad とおくと$
$\quad f'(t)=\cfrac{4(t+1)(t+9)-4t(t+9+t+1)}{(t+1)^2(t+9)^2}=\cfrac{-4(t^2-9)}{(t+1)^2(t+9)^2}=\cfrac{-4(t+3)(t-3)}{(t+1)^2(t+9)^2}$
\[
\begin{array}{c||c|c|c|c|c}
\hline
t& 0 & \cdots & 3 & \cdots \\
\hline
f'(t) & & + & 0 & - & \\
\hline
f(t)& & \nearrow & 極大 & \searrow & \\
\hline
\end{array}
\]
$\quad t=3 \ で \ f(t)\ は最大となり、最大値は \quad f(3)=\cfrac{12}{4 \times 12}=\cfrac{1}{4}$
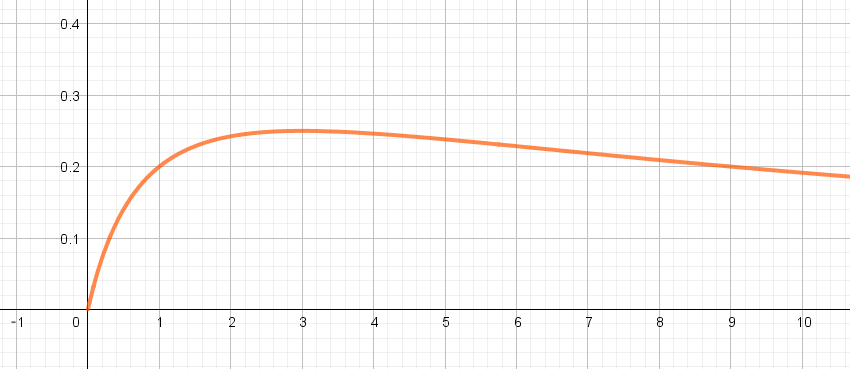
$\quad 右図は、f(t)\ のグラフです。$
メインメニュー に戻る