神戸大学(理系) 2020年 問題4
$nを自然数とし、2n\pi \leqq x \leqq (2n+1)\pi \ \ に対して \ f(x)=\cfrac{\sin x}{x}\ \ とする。以下の問いに答えよ。$
$\qquad (1)\ \ f(x)が最大となるxの値がただ1つ存在することを示せ。$
\[(2)\ \ (1)のxの値をx_n とする。このとき、\lim _{n \rightarrow \infty} \cfrac{n}{\tan x_n} を求めよ。\]
$(解説)$
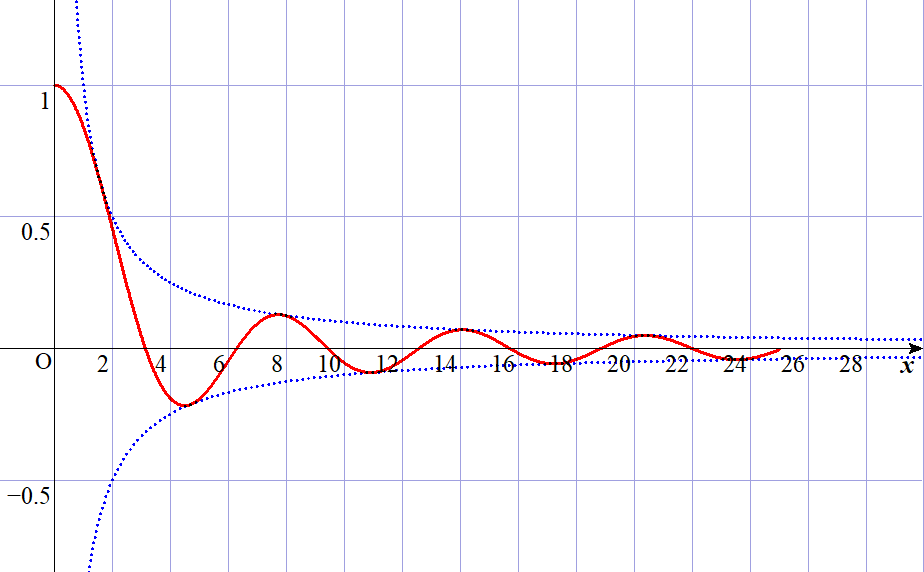
$(1)はこのグラフが、\pm \cfrac{1}{x}の中に収まっていることがわかれば概形が描けるので、問題の意図が読み取れます。$
$\quad ある区間で、F(x)=0を満たすxの値がただ1つ存在することをの証明は、この区間でグラフが単調で、$
$\quad 値が正負入れ代わることを示せば、中間値の定理が保証してくれます。$
$(2)のポイントは、\cfrac{n}{\tan x_n} \ \ を \ \ \cfrac{n}{x_n}\ \ で代替することです。$
(1)
$f(x)=\cfrac{\sin x}{x}\ \ より \quad f'(x)=\cfrac{x\cos x -\sin x}{x^2}$
$g(x)=x\cos x -\sin x \quad とおくと$
$g(2n\pi)=2n\pi \cos 2n\pi - \sin 2n\pi=2n\pi > 0$
$g((2n+1)\pi)=(2n+1)\pi \cos (2n+1)\pi - \sin (2n+1)\pi$
$\hspace{6em} =-(2n+1)\pi$
$\hspace{6em} < 0$
$g'(x)=\cos x -x\sin x-\cos x=-x\sin x$
$\quad 2n\pi \leqq x \leqq (2n+1)\pi \ \ で \quad g'(x) < 0$
$よって g(x)\ はこの区間で単調減少する。$
$したがって、中間値の定理より、この区間で \ \ g(x)=0\quad すなわち \quad f'(x)=0\quad となるxが$
$ただ1つ存在するからこれを\alpha とおく。$
$f(x)\ の増減表は$
\[
\begin{array}{c||c|c|c|c|c}
\hline
x& 2n\pi&\cdots&\alpha &\cdots&(2n+1)\pi\\
\hline
f'(x)& &+&0&-& \\
\hline
f(x)& &\nearrow&極大&\searrow& \\
\hline
\end{array}
\]
$f(x)\ は \ \ x =\alpha \ \ で極大かつ最大となる。$
(2)
$\alpha =x_n \ \ とおくと \quad x_n\cos x_n -\sin x_n=0 \quad \therefore x_n=\tan x_n$
$よって \quad \cfrac{n}{\tan x_n}=\cfrac{n}{x_n}$
$2n\pi < x_n < (2n+1)\pi \quad だから \quad \cfrac{n}{(2n+1)\pi} < \cfrac{n}{x_n} < \cfrac{n}{2n\pi}=\cfrac{1}{2\pi}$
$n \rightarrow +\infty \ \ のとき \quad \cfrac{n}{(2n+1)\pi}=\cfrac{1}{(2+\cfrac{1}{n})\pi} \rightarrow \cfrac{1}{2\pi}$
\[したがって \qquad \lim _{n \rightarrow \infty} \cfrac{n}{x_n} =\cfrac{1}{2\pi} \quad だから \quad \lim _{n \rightarrow \infty} \cfrac{n}{\tan x_n} =\cfrac{1}{2\pi}\]
メインメニュー に戻る