金沢大学(理系) 2025年　問題3


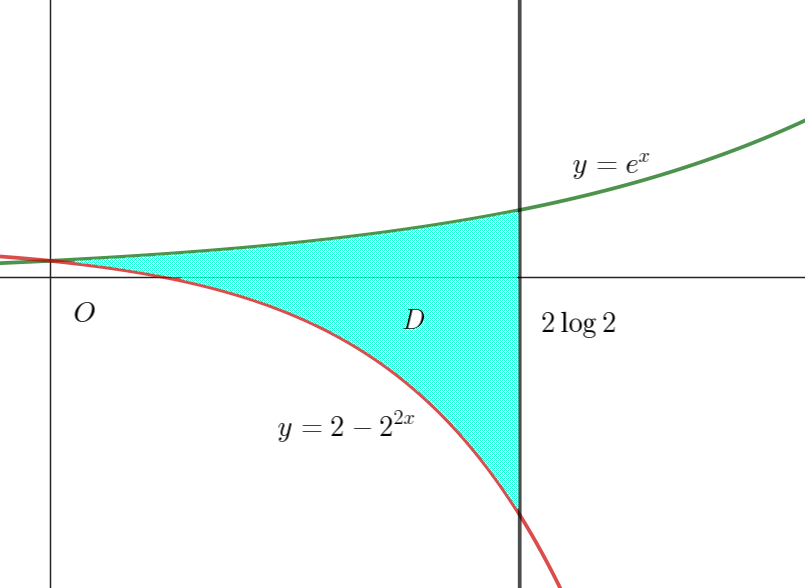
$座標平面上の\ \ 0 \leqq x \leqq 2\log 2 \ \ の範囲において、曲線 \ y=e^x \ \ と曲線 \ y=2-e^{2x},\ \ 直線 \ x=2\log 2\ \ で囲まれた$
$図形を \ D\ とする。図形 \ D\ を \ x\ 軸の周りに \ 1\ 回転してできる回転体の体積 \ V\ を求めよ。$

　

$図形 \ D\ は右図のとおりである。$

$y=2-e^{2x}\ \ を \ x\ 軸について対称移動(折り返した)グラフは$

$-y=2-e^{2x} \ \ だから \quad y=-2+e^{2x}$

(i)$\ \ y=2-e^{2x}\ \ と \ x\ 軸の交点は$

$\quad 2-e^{2x}=0 \ \ より \quad e^{2x}=2$

$\quad 2x=\log 2 \qquad \therefore \ \ x=\dfrac{1}{2}\log 2$

(ii)$\ \ y=e^x \ \ と\ \ y=-2+e^{2x}\ \ の交点は$

$\quad e^x=-2+e^{2x} \ \ より \quad e^{2x}-e^x-2=0$

$\quad (e^x+1)(e^x-2)=0 \qquad e^x+1 > 0 \quad だから$

$\quad e^x=2 \qquad \therefore \ \ x=\log 2$

(iii)$\ \ x=2\log 2 \ \ との交点は$

$\quad y=e^x \ \ では \quad y=e^2{\log 2}=4$

$\quad y=-2+e^{2x} \ \ では \quad y=-2+e^{4\log 2}=-2+16=14$

　

$y=e^x \ \ と \ \ y=-2+e^{2x}\ \ はともに単調増加だから$

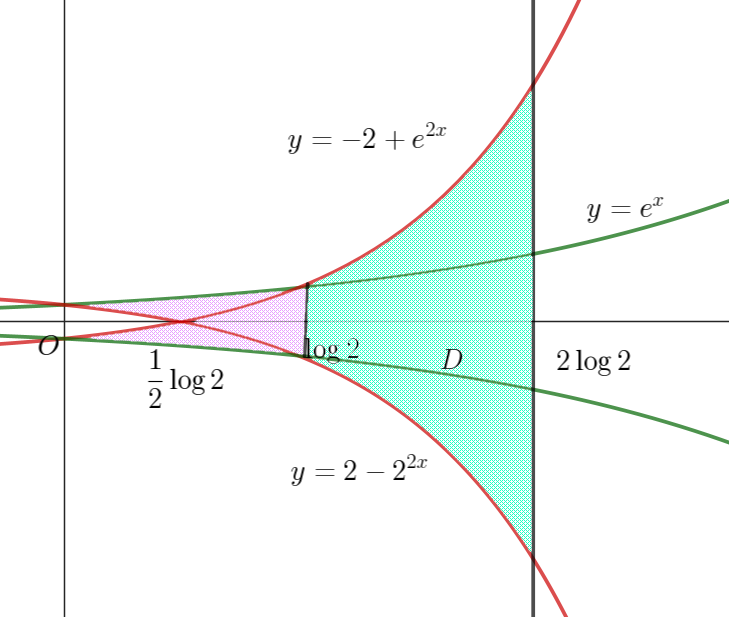
$曲線 \ y=e^x \ \ と曲線 \ y=2-e^{2x}\ \ の位置関係は右図のとおりで$

$0 \leqq x \leqq \log 2 \ \ では \quad e^x \geqq -2+e^{2x}$

$\log 2 \leqq x \leqq 2\log 2 \ \ では \quad e^x \leqq -2+e^{2x} $

$したがって、図形 \ D\ を \ x\ 軸の周りに \ 1\ 回転してできる回転体の$

$体積 \ V\ は$

\begin{eqnarray*} V &=&\pi\int_0^{\log 2} (e^x)^2dx - \pi\int_0^{\frac{1}{2}\log 2} (-2+2^{2x})^2dx + \pi\int_{\log 2}^{2\log 2}(-2+e^{2x})^2dx\\ \\ &=&\pi\int_0^{\log 2} e^{2x}dx - \pi\int_0^{\frac{1}{2}\log 2} (4-4e^{2x}+e^{4x})dx + \pi\int_{\log 2}^{2\log 2}(4-4e^{2x}+e^{4x})dx\\ \\ &=&\pi\Big[\dfrac{1}{2} e^{2x}\Big] _0^{\log 2} - \pi \Big[4x-2e^{2x}+\dfrac{1}{4}e^{4x}\Big]_0^{\frac{1}{2}\log 2} + \pi\Big[4x-2e^{2x}+\dfrac{1}{4}e^{4x}\Big] _{\log 2}^{2\log 2}\\ \\ &=&\dfrac{\pi}{2}\big(e^{2\log 2}-1\big) - \pi \big(2\log 2-2e^{\log 2}+\dfrac{1}{4}e^{2\log 2}+2-\dfrac{1}{4}\big) + \pi\big( 8\log 2 -2e^{4\log 2}+\dfrac{1}{4}e^{8\log 2}-4\log 2+2e^{2\log 2} -\dfrac{1}{4}e^{4\log 2}\big)\\ \\ &=&\dfrac{\pi}{2}(4-1) - \pi (2\log 2-2 \times 2 +\dfrac{1}{4} \times 4 +2-\dfrac{1}{4}) + \pi( 8\log 2 -2 \times 16 +\dfrac{1}{4} \times 2^8 -4\log 2+2 \times 4 -\dfrac{1}{4} \times 16)\\ \\ &=&\big(\dfrac{155}{4}+2\log 2\big)\pi \end{eqnarray*}

ページの先頭へ↑



メインメニュー　に戻る