金沢大学(理系) 2025年 問題2
$実数 \ a>0 \ \ に対し、座標平面上の点P(a,\ 0)をとる。曲線 \ \ y=\dfrac{1}{3}x^{\frac{3}{2}}\ \ (x \geqq 0) \ \ を \ C\ とする。点Q\ が曲線C\ 上を$
$動くとき、PQ^2\ \ の最小値を与える点Q\ の \ x\ 座標を \ F(a)\ とし、PQ^2\ の最小値を \ G(a)\ とする。$
$次の問いに答えよ。$
$(1)\ \ F(a)\ \ を求めよ。$
\[(2)\ \ \lim_{a \rightarrow +0} \dfrac{F(a)-a}{a^2}\ \ を求めよ。\]
\[(3)\ \ \lim_{a \rightarrow +0} \dfrac{G(a)}{a^3} \ \ を求めよ。\]
(1)
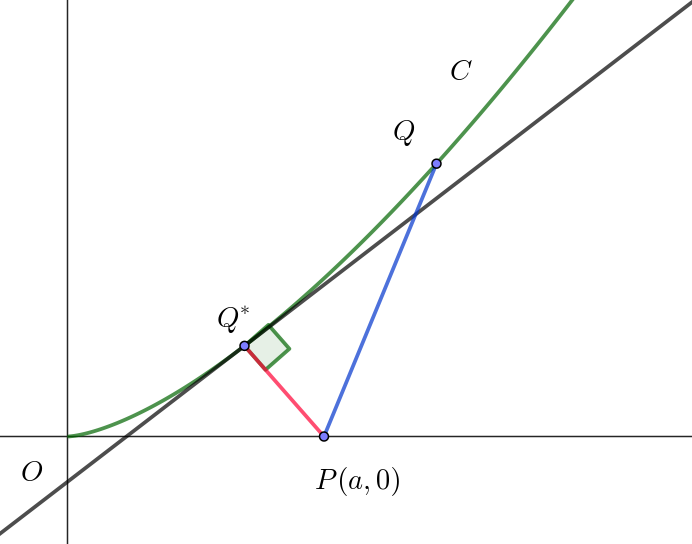
$PQ^2=(t-a)^2+\big(\dfrac{1}{3}t^{\frac{3}{2}}\big)^2=(t-a)^2+\dfrac{1}{9}t^3$
$PQ^2=f(t) \quad とおくと$
$f(t)=\dfrac{1}{9}t^3+t^2-2at+a^2$
$f'(t)=\dfrac{1}{3}t^2+2t-2a$
$f'(t)=0 \ \ より \quad t^2+6t-6a=0$
$この正の解を \ \alpha \ \ とおくと \quad \alpha =-3+\sqrt{9+6a}$
$増減表$
\[ \begin{array}{c||c|c|c|c|c} t& 0 & \cdots & \alpha & \cdots \\ \hline f'(t)& & - & 0 & + & \\ \hline f(t)& & \searrow & 極小 & \nearrow & \\ \end{array} \]
$f(t)\ \ は \ \ t=\alpha \ \ で極小かつ最小だから$
$F(a)=-3+\sqrt{9+6a}$
$(補充)$
$Q(t,\ \dfrac{1}{3}t^{\frac{3}{2}})\ \ における曲線C\ の法線は$
$y=-2t^{-\frac{1}{2}}(x-t)+\dfrac{1}{3}t^{\frac{3}{2}}$
$これが \ P(a,\ 0)\ \ を通るから$
$-2t^{-\frac{1}{2}}(a-t)+\dfrac{1}{3}t^{\frac{3}{2}}=0$
$両辺に \ \ 3t^{\frac{1}{2}}\ \ をかけて \quad -6(a-t)+t^2=0$
$t^2+6t-6a=0$
$これは上の解答の導関数と同じ式である。$
(2)
\begin{eqnarray*} & &\dfrac{F(a)-a}{a^2}\\ \\ &=&\dfrac{-3+\sqrt{9+6a}-a}{a^2}\\ \\ &=&-\dfrac{a+3-\sqrt{9+6a}}{a^2}\\ \\ &=&-\dfrac{(a+3)^2-(9+6a)}{a^2(a+3+\sqrt{9+6a})}\\ \\ &=&-\dfrac{a^2}{a^2(a+3+\sqrt{9+6a})}\\ \\ &=&-\dfrac{1}{a+3+\sqrt{9+6a}}\\ \end{eqnarray*} $よって$
\[\quad \lim_{a \rightarrow +0} \dfrac{F(a)-a}{a^2}=-\dfrac{1}{3+\sqrt{9}}=-\dfrac{1}{6}\]
(3)
$f(t)=\dfrac{1}{9}t^3+t^2-2at+a^2 \ \ を \ \ f'(t)=\dfrac{1}{3}t^2+2t-2a \ \ で割った商を \ Q(t)、余りを \ R(t) \ とすると$
$筆算の割り算を行って \quad Q(t)=\dfrac{1}{3}t+1,\qquad R(t)=-(\dfrac{4}{3}a+2)t+a^2+2a$
$f(t)=f'(t)Q(t)+R(t)\ \ に \ \ t=\alpha \ \ を代入して$
$f(\alpha)=f'(\alpha)Q(\alpha)+R(\alpha) $
$G(a)=f(\alpha), \quad f'(\alpha)=0 \quad だから$
\begin{eqnarray*} G(a) &=&R(\alpha)\\ \\ &=&(\dfrac{4}{3}a+2)\alpha+a^2+2a\\ \\ &=&-(\dfrac{4}{3}a+2)(-3+\sqrt{9+6a})+a^2+2a\\ \\ &=&a^2+6a+6-(\dfrac{4}{3}a+2)\sqrt{9+6a}\\ \end{eqnarray*}
\begin{eqnarray*} \dfrac{G(a)}{a^3} &=&\dfrac{a^2+6a+6-(\dfrac{4}{3}a+2)\sqrt{9+6a}}{a^3}\\ \\ &=&\dfrac{(a^2+6a+6)^2-(\dfrac{4}{3}a+2)^2(9+6a)}{a^3\{a^2+6a+6+(\dfrac{4}{3}a+2)\sqrt{9+6a}\}}\\ \\ &=&\dfrac{(a^2+6a+6)^2-(\dfrac{16}{9}a^2+\dfrac{16}{3}a+4)(9+6a)}{a^3\{a^2+6a+6+(\dfrac{4}{3}a+2)\sqrt{9+6a}\}}\\ \\ &=&\dfrac{a^4+\dfrac{4}{3}a^3}{a^3\{a^2+6a+6+(\dfrac{4}{3}a+2)\sqrt{9+6a}\}}\\ \\ &=&\dfrac{a+\dfrac{4}{3}}{a^2+6a+6+(\dfrac{4}{3}a+2)\sqrt{9+6a}}\\ \end{eqnarray*} $よって$
\[\quad \lim_{a \rightarrow +0} \dfrac{G(a)}{a^3}=-\dfrac{\dfrac{4}{3}}{6+2\sqrt{9}}=\dfrac{1}{9}\]
メインメニュー に戻る