金沢大学(理系) 2023年　問題2


$座標空間において、平面 \ z=2\ 上の点 \ P\ と、平面 \ z=1\ 上の円板 \ B:x^2+y^2 \leqq 1,\ \ z=1\ を考える。$
$点 \ Q\ は平面 \ z=0\ (xy\ 平面)\ 上にあるとし、与えられた \ P\ に対して、線分 \ PQ\ と \ B\ が共有点をもつ$
$ような \ Q\ 全体からなる図形を \ D\ とする。次の問いに答えよ。$
$(1)\ \ P\ の座標が \ (0,\ 0,\ 2)\ であるとき、D\ を \ xy\ 平面上に図示せよ。$
$(2)\ \ r\ を正の定数とする。P\ の座標が \ (r,\ 0,\ 2)\ であるとき、D\ を \ xy\ 平面上に図示せよ。$
$(3)\ \ r > 2\ を満たす定数 \ r\ に対して、平面 \ z=2 \ 上の円 \ C:x^2+y^2=r^2,\ \ z=2\ を考える。P\ が \ C\ 上を$
$\quad 動くとき、D\ が通過する部分の面積を求めよ。$


(1)

　

$平面 \ z=1\ 上の円 \ x^2+y^2 =1 \ の中心を \ E(0\ ,0,\ 1)\ とし、$

$円周上の任意の点を \ R\ とする。$

$直線 \ PR\ と \ xy\ 平面の交点を \ Q\ とすると$

$\triangle PER \sim \triangle POQ \quad だから$

$PE:PO=ER:OQ \qquad 1:2=1:OQ \qquad OQ=2$

$点 \ R\ が半径 \ 1\ の円周上を動くと、点 \ Q\ は半径 \ 2\ の円をえがく。$

　

$よって、点 \ R\ が円板 \ B\ 内を動くと、点 \ Q\ は原点中心、半径 \ 2\ の円板をえがく。$

$その図は右のとおりである。$


(2)


$B:\ x^2+y^2 \leqq 1,\ \ z=1\ をみたす点 \ R\ は$

$R(a\cos \theta,\ a\sin \theta,\ 1)\ \ (0 \leqq a \leqq 1)\ \ とおける。$

$P(r,\ 0,\ 2),\ \ Q(x,\ y,\ 0)\ \ とおくと \ 3\ 点 \ P,\ Q,\ R\ は一直線上にあるから$

$\vec{PQ}=k\vec{PR}\ \ をみたす実数 \ k\ が存在する。$

　


$\vec{OQ}-\vec{OP}=k(\vec{OR}-\vec{OP})$

$(x,\ y,\ 0)-(r,\ 0,\ 2)=k\{(a\cos \theta,\ a\sin \theta,\ 1)-(r,\ 0,\ 2)\}$

$(x-r,\ y,\ -2)=k(a\cos \theta-r,\ a\sin \theta ,\ -1)$
\[ \hspace{1em} \left\{ \begin{array}{l} x-r=k(a\cos \theta -r) \hspace{5.5em}①\\ y=ka\sin \theta \hspace{10em}②\\ -2=-k \hspace{11em}③\\ \end{array} \right. \]
$③より \quad k=2$

$①に代入して \quad x+r=2a\cos \theta$

$②に代入して \quad y=2a\sin \theta$

$\therefore \ \ (x+r)^2+y^2=4a^2 $

　

$0 \leqq a \leqq 1 \quad だから \quad 　(x+r)^2+y^2 \leqq 4$

$これは、中心(-r,\ 0),\ \ 半径 \ 2\ の円であるが$

$2-r > 0,\ \ 2-r=0,\ \ 2-r <0 \ \ によって円とy \ 軸は、$

$それぞれ、2\ 点で交わる、接する、交わらない 。$

$右図は \ \ r < 2 \ \ の場合の図である。$


(3)

　

$B:\ x^2+y^2 \leqq 1,\ \ z=1\ をみたす点 \ R\ は$

$R(a\cos \theta,\ a\sin \theta,\ 1)\ \ (0 \leqq a \leqq 1)\ \ とおける。$

$C:\ x^2+y^2 =r^2 ,\ \ z=2\ \ をみたす点 \ P\ は$

$P(r\cos \varphi,\ r\sin \varphi,\ 2)\ \ とおける。$

$Q(x,\ y,\ 0)\ とおくと \ 3\ 点 \ P,\ Q,\ R\ は一直線上にあるから$

$\vec{PQ}=t\vec{PR} \ \ をみたす実数 \ t\ が存在する。$

$\vec{OQ}-\vec{OP}=t(\vec{OR}-\vec{OP})$

$(x,\ y,\ 0)-(r\cos \varphi,\ r\sin \varphi,\ 2) =t\{(a\cos \theta,\ a\sin \theta,\ 1)-(r\cos \varphi,\ r\sin \varphi,\ 2)\}$

$(x-r\cos \varphi,\ y-r\sin \varphi,\ -2)=t(a\cos \theta-r\cos \varphi,\ a\sin \theta -r\sin \varphi,\ -1)$
\[ \hspace{1em} \left\{ \begin{array}{l} x-r\cos \varphi =t(a\cos \theta-r\cos \varphi) \hspace{5em}①\\ y-r\sin \varphi =t(a\sin \theta -r\sin \varphi) \hspace{5.5em}②\\ -2=-t \hspace{15em}③\\ \end{array} \right. \]
$③より \quad t=2$

$①に代入して \quad x+r\cos \varphi=2a\cos \theta $

$②に代入して \quad y+r\sin \varphi=2a\sin \theta $

$\therefore \ \ (x+r\cos \varphi)^2+(y+r\sin \varphi)^2=4a^2 $

　

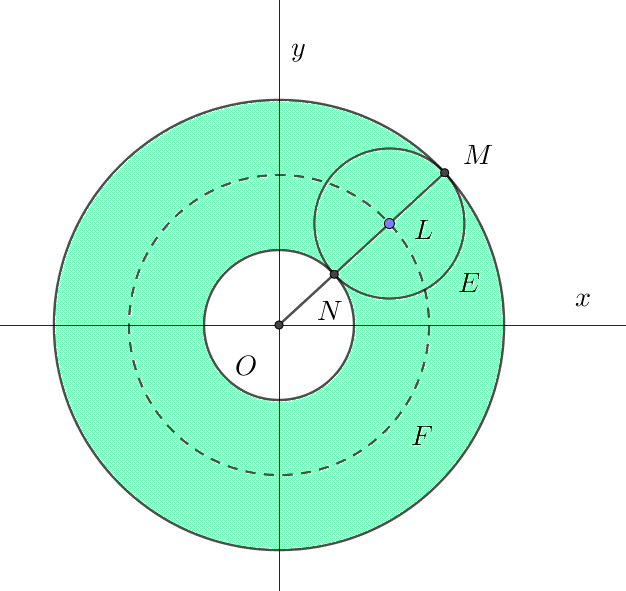
$点 \ Q\ は L(-r\cos \varphi,\ -r\sin \varphi)\ \ を中心に半径 \ 2a\ の円Eをえがく。$

$L(-r\cos \varphi,\ -r\sin \varphi)\ \ の軌跡は$

$x=-r\cos \varphi, \quad y=-r\sin \varphi \quad とおくと \quad x^2+y^2=r^2$

$L\ は原点中心、半径 \ r\ の円 \ F\ をえがく。$

$2a < 2 ,\quad r > 2\ \ だから \ 2\ 円の位置関係は右図のとおりである。$

$円 \ C\ 上の \ 1\ 点 \ P\ に対して、xy\ 平面上に円板 \ D\ が \ 1\ つ定まり、$

$点 \ P\ は連続的に移動するから、円板 \ D\ も連続的に移動する。$

$したがって、0 \leqq a \leqq 1 \quad だから\ \ D\ が通過する部分は図の緑色の領域である。$

$その面積を \ S\ とする。$

$直線 \ OL\ と円 \ E,\ F\ の交点をそれぞれ \ M,\ N\ \ とおくと、a=1\ の点だから$

$OM=OL+LM=r+2,\quad ON=OL-LN=r-2$

$よって$

\begin{eqnarray*} S &=&\pi OM^2-\pi ON^2\\ \\ &=&\pi(r+2)^2-\pi(r-2)^2\\ \\ &=&8\pi r\\ \end{eqnarray*}

ページの先頭へ↑



メインメニュー　に戻る