MY MATH NOTE

金沢大学（理系）2019年前期　問題3

$座標平面において、$
$\qquad x=\sin t,\quad y=\cos t-\sin t \quad (0 \leqq t \leqq 2\pi)$
$で表される曲線をC_1とし、x軸に関してC_1と対称な曲線をC_2 とする。C_1で囲まれる図形と$
$C_2で囲まれる図形の共通部分の面積Sを求めよ。$

　
$y=\cos t -x \ \ より \ \ \cos t=x+y$
$\sin ^2 t+\cos ^2 t=1 \ \ に代入して \quad x^2+(x+y)^2=1$
$\therefore \ \ 2x^2+2xy+y^2=1 \hspace{20em}(1)$

$\quad (この形の2次曲線については($2次曲線の標準化$)を参照してください。)$

$判別式は \quad D=1^2-2 \times 1=-1 \ \ で負だからC_1は$
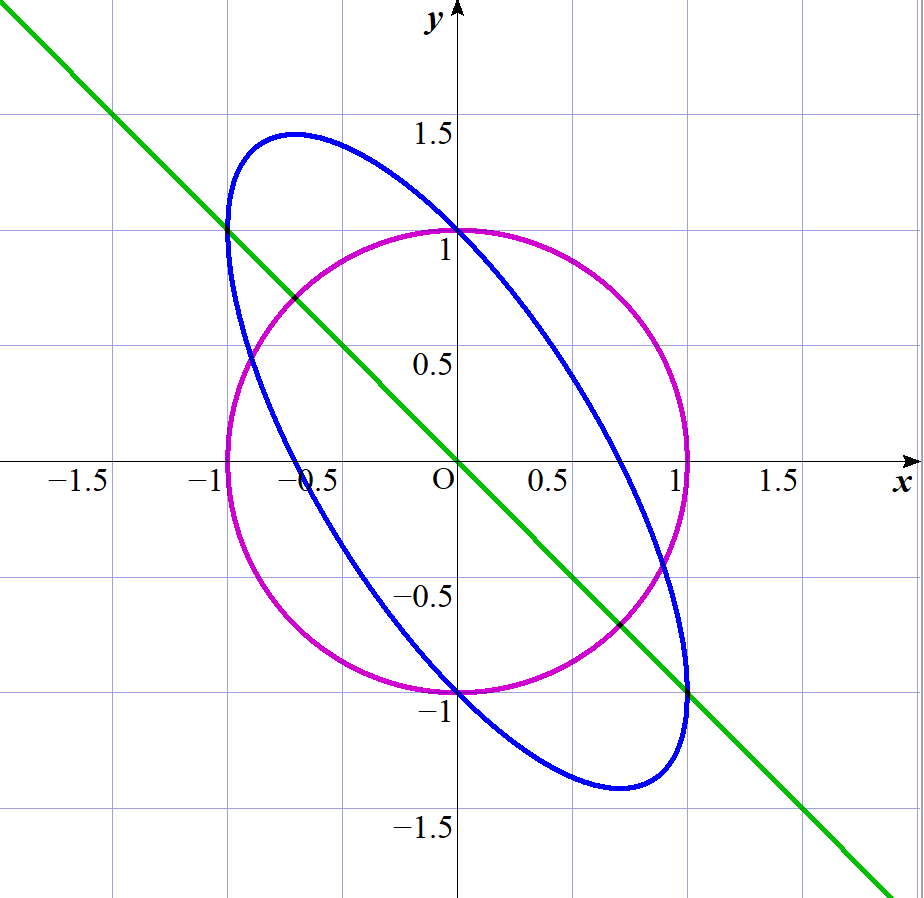
$右図の青色の楕円を表します。$
$その根拠は5行下にあります。$

$これをx軸に関して対称移動したC_2は赤色の楕円です。$

$xy \ の項を消去するには、原点の回りに、\tan \theta =\cfrac{2}{2-1}=2 \ \ をみたす\theta $
$だけ座標軸を回転する必要がありますが、\theta がいい値で求まりませんので、$
$XY表示は無理に求めることはないでしょう。$

　
$y\ について解くと$

$\qquad y=-x \pm \sqrt{1-x^2} $

$これは \ \ y=-x \ \ (図の緑の直線)と \ \ y=\pm \sqrt{1-x^2} \ \ (図の紫色の円)$
$の和ですから、青色の楕円になるわけです。$

$曲線(1)のx軸に関する対称移動は \quad y \longrightarrow -y \ \ とおいて$

$\quad 2x^2-2xy+y^2=1 \hspace{20em}(2)$

$yについて解くと \quad y=x \pm \sqrt{1-x^2}$

$C_1とC_2はともにx軸、y軸について対称だから第1象限で考えれば十分です。$

$図はグラフソフトを使って正確に描きましたが、$

$\quad (x+\sqrt{1-x^2})-(-x+\sqrt{1-x^2}=2x > 0$

$よって、C_2がC_1より上にあるので、第1象限での共通部分はC_1で囲まれた領域となります。$

\begin{eqnarray*} S &=&4\times \int _0^{\small{\dfrac{1}{\sqrt{2}}}}(-x+\sqrt{1-x^2})dx\\ &=&-4\int _0^{\small{\dfrac{1}{\sqrt{2}}}}xdx+4\int _0^{\dfrac{1}{\small{\sqrt{2}}}}\sqrt{1-x^2}dx\\ \end{eqnarray*} $第1項=-4\bigl[\cfrac{x^2}{2}\bigr]_0^{\small{\dfrac{1}{\sqrt{2}}}}=-1$

$第2項の積分を \ I\ とおき、x=\sin \theta \ \ と変換すると$
\[dx=\cos \theta d\theta \qquad \begin{array}{c|c} x& 0 \rightarrow \small{\dfrac{1}{\sqrt{2}}} \\ \hline \theta & 0 \rightarrow \small{\dfrac{\pi}{4}} \\ \end{array} \] \begin{eqnarray*} I &=&\int _0^{\small{\dfrac{\pi}{4}}} \sqrt{1-\sin ^2 \theta }\cos \theta \ d\theta\\ &=&\int _0^{\small{\dfrac{\pi}{4}}} \cos ^2 \theta \ d\theta \\ &=&\cfrac{1}{2}\int _0^{\small{\dfrac{\pi}{4}}} (1+\cos 2\theta )d\theta \\ &=&\cfrac{1}{2}\bigl[\theta +\cfrac{1}{2}\sin 2\theta \bigr]_0^{\small{\dfrac{\pi}{4}}}\\ &=&\cfrac{1}{2}\left(\small{\dfrac{\pi}{4}+\cfrac{1}{2}}\right)\\ \end{eqnarray*} $よって$
\begin{eqnarray*} S &=&-1+4\times \cfrac{1}{2}\left(\small{\dfrac{\pi}{4}+\cfrac{1}{2}}\right)\\ &=&\dfrac{\pi}{2}\\ \end{eqnarray*}

　
$なお、第2項の積分は右図の扇形と直角三角形の面積の和だから$
\begin{eqnarray*} I &=&扇形OBC \ + △OAB\\ &=&\pi \times 1^2 \times \cfrac{1}{8}+\cfrac{1}{2} \times \cfrac{1}{\sqrt{2}}\times \cfrac{1}{\sqrt{2}}\\ &=&\cfrac{\pi}{8}+\cfrac{1}{4}\\ \end{eqnarray*} $と求めてもよいでしょう。$

ページの先頭へ↑