北海道大学(理系) 2021年 問題5
$座標平面上で、媒介変数 \ \theta \ を用いて \quad x=(1+\cos \theta)\cos \theta ,\quad y=\sin \theta \ \ (0 \leqq \theta \leqq \pi)\ \ と表される曲線 \ C\ がある。$
$C\ 上の点で \ x\ 座標の値が最小になる点を \ A\ とし、A\ の \ x\ 座標の値を \ a\ とおく。B\ を点 \ (a,\ 0),\ O\ を原点 \ (0,\ 0)$
$とする。$
$\quad (1)\ \ a\ を求めよ。$
$\quad (2)\ \ 線分 \ AB\ と線分 \ OB\ と \ C\ で囲まれた部分の面積を求めよ。$
$(解説)$
$(1)は単に最小値を求めるだけの問題です。$
$(2)は曲線Cの概形が描ければ、置換積分で求まります。$
(1)
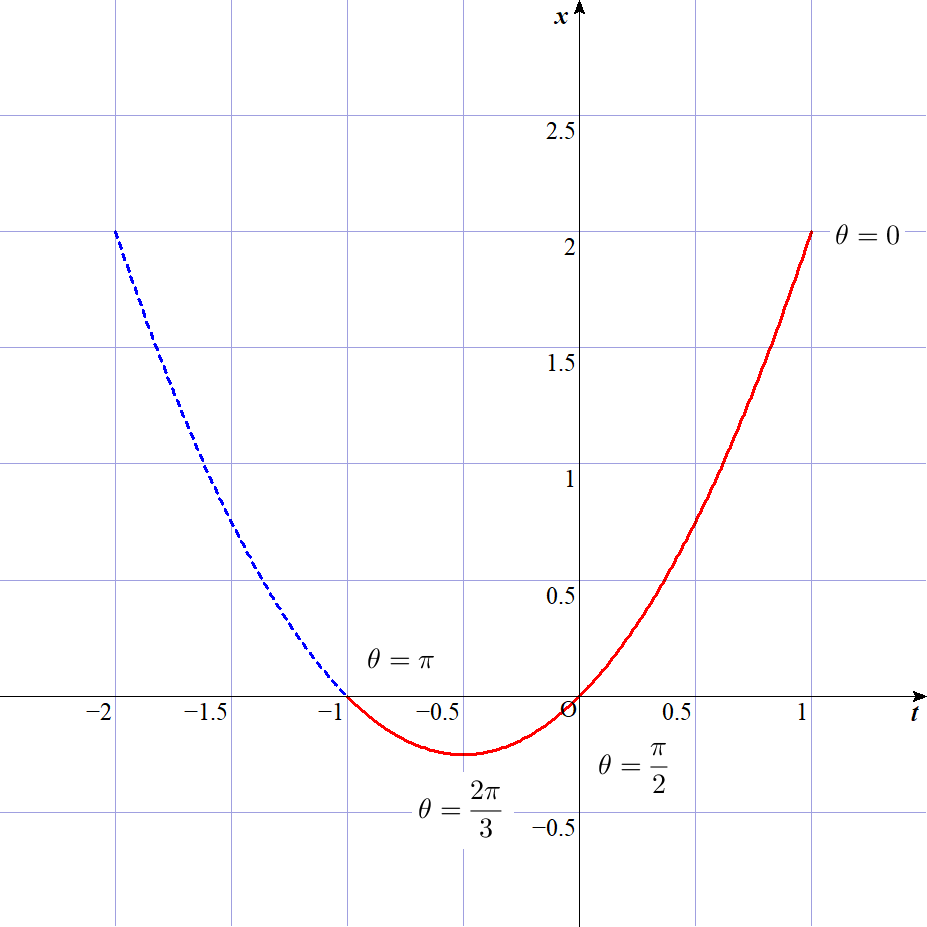
$x=(1+\cos \theta)\cos \theta =\cos ^2 \theta +\cos \theta =(\cos \theta +\cfrac{1}{2})^2-\cfrac{1}{4}$
$\quad t=\cos \theta \ \ とおくと \quad x=(t+\cfrac{1}{2})^2- \cfrac{1}{4}$
$\quad 0 \leqq \theta \leqq \pi \quad より \quad -1 \leqq t \leqq 1$
$グラフは右図のとおりで$
$\quad t=-\cfrac{1}{2} \ \ のとき \ \ x \ は最小値 \ \ -\cfrac{1}{4}\ \ をとる。$
$よって \quad a=-\cfrac{1}{4}$
$なお、このとき \quad \cos \theta =-\cfrac{1}{2} \quad より \quad \theta =\cfrac{2}{3}\pi$
(2)
$\theta \ \ の変化による \ x\ の増減は上のグラフより、y\ の増減は \ \ y=\sin \theta \ \ より下表のように求まる。$
\[ \begin{array}{c||c|c|c|c|c} \hspace{2em}\theta \hspace{2em} & 0 & \cdots & \cfrac{\pi}{2} & \cdots & \cfrac{2\pi}{3} & \cdots & \pi\\ \hline xの増減 \ \ & & - & & - & & + &\\ \hline yの増減 \ \ & & + & & - & & - &\\ \hline x & 2 & \searrow & 0 & \searrow & -\cfrac{1}{4} & \nearrow & 0 \\ \hline y & 0 & \nearrow & 1 & \searrow & \cfrac{\sqrt{3}}{2} & \searrow & 0 \\ \end{array} \]
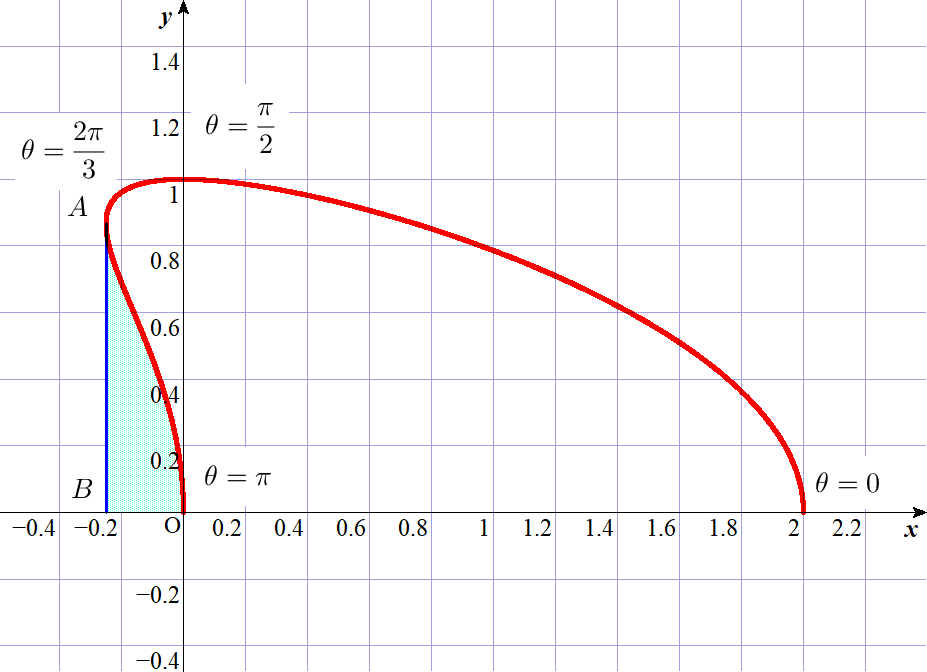
$この増減表よりグラフが描けますが、グラフ作成ソフトによる$
$曲線Cのグラフは右図のとおりです。$
$求める面積 \ S\ は水色の領域の面積です。$
$\quad x=(1+\cos \theta)\cos \theta \quad より$
$\quad dx=\{-\sin \theta \cos \theta -(1+\cos \theta )\sin \theta \}d\theta=-\sin \theta (1+2\cos \theta )d\theta$
\[
\quad
\begin{array}{c|c}
x & -\cfrac{1}{4}\ \ \rightarrow 0 \quad \\
\hline
\theta & \cfrac{2\pi}{3} \ \rightarrow \pi \\
\end{array}
\]
\begin{eqnarray*}
S
&=&\int _{\small{-\cfrac{1}{4}}}^{\large{0}} y dx\\
&=&\int _{\small{\cfrac{2\pi}{3}}}^{\large{\pi}} \sin \theta (-\sin \theta )(1+2\cos \theta )d\theta \\
\\
&=&-\int _{\small{\cfrac{2\pi}{3}}}^{\large{\pi}} \sin ^2 \theta d\theta -2\int _{\small{\cfrac{2\pi}{3}}}^{\large{\pi}} \sin ^2 \theta \cos \theta d\theta \\
\end{eqnarray*}
\[第1項=-\int _{\small{\cfrac{2\pi}{3}}}^{\large{\pi}} \sin ^2 \theta d\theta =-\cfrac{1}{2}\int _{\small{\cfrac{2\pi}{3}}}^{\large{\pi}} (1-\cos 2\theta) d\theta
=-\cfrac{1}{2}\big[\theta -\cfrac{\sin 2\theta}{2}\big]_{\small{\cfrac{2\pi}{3}}}^{\large{\pi}}=\cfrac{\sqrt{3}}{8}-\cfrac{\pi}{6}\]
\[
第 \ 2\ 項は \quad \sin \theta =u \quad とおくと \quad \cos \theta d\theta =du \qquad
\begin{array}{c|c}
\theta & \cfrac{2\pi}{3} \ \rightarrow \pi \\
\hline
u & \cfrac{\sqrt{3}}{2}\ \ \rightarrow 0 \quad \\
\end{array}
\]
\[第2項=-2\int _{\small{\cfrac{\sqrt{3}}{2}}}^{\large{0}} u^2 du=-2\big[\cfrac{t^3}{3}\big]_{\small{\cfrac{\sqrt{3}}{2}}}^{\large{0}}=\cfrac{\sqrt{3}}{4}\]
$よって \quad S=(\cfrac{\sqrt{3}}{8}-\cfrac{\pi}{6})+\cfrac{\sqrt{3}}{4}=\cfrac{3\sqrt{3}}{8}-\cfrac{\pi}{6}$
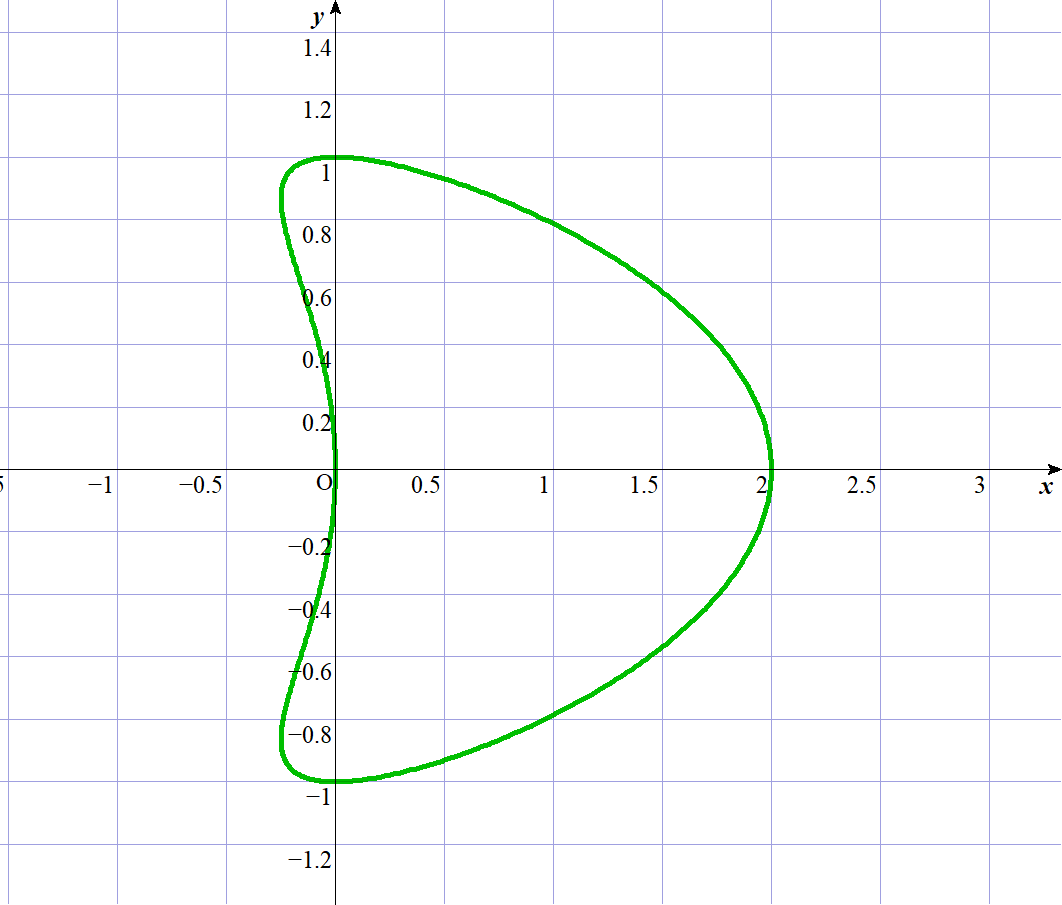
$(補充)$
$0 \leqq \theta \leqq 2\pi \ \ としたときの曲線 \ C\ のグラフは$
$x軸に関して対称になります。$
メインメニュー に戻る