MY MATH NOTE

北海道大学(理系) 2021年　問題1

$三角形 \ OAB\ において、辺 \ AB\ を \ 2:1\ に内分する点を \ D\ とし、直線 \ OA\ に関して点 \ D\ と対称な点を$
$E\ とする。\vec{OA}=\vec{a},\ \ \vec{OB}=\vec{b}\ とし、|\vec{a}|=4,\ \ \vec{a}\cdot \vec{b}=6\ \ を満たすとする。$
$\quad (1)\ \ 点 \ B\ から直線 \ OA\ に下ろした垂線と直線 \ OA\ との交点を \ F\ とする。\vec{OF}\ を \ \vec{a}\ を用いて表せ。$
$\quad (2)\ \ \vec{OE}\ を \ \vec{a},\ \vec{b}\ を用いて表せ。$
$\quad (3)\ \ 三角形 \ BDE\ の面積が \ \ \cfrac{5}{9}\ \ になるとき、|\vec{b}|\ の値を求めよ。$

(1)

　
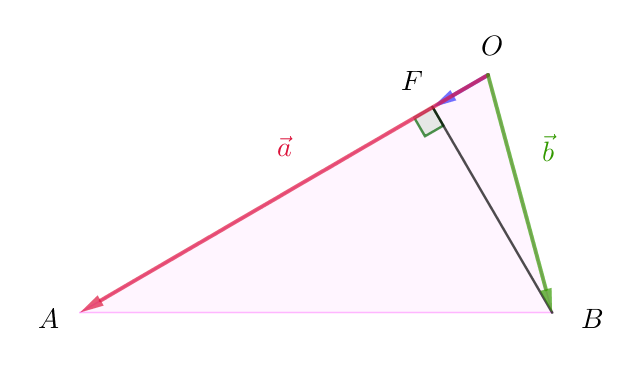
$\angle AOB=\theta \ \ とおくと \quad \vec{a}\cdot \vec{b}=|\vec{a}||\vec{b}|\cos \theta =6 \quad より$

$\cos \theta > 0 \quad \therefore \ \ 0 < \theta < \cfrac{\pi}{2}$

$よって、点 \ F\ は線分 \ OA\ 上にあるから、k\ は正の実数として$

$\vec{OF}=k\vec{a}\quad とおける。$

$\vec{BF}=\vec{OF}-\vec{OB}=k\vec{a}-\vec{b}$

$BF \perp OF \quad より \quad (k\vec{a}-\vec{b}) \cdot k\vec{a}=0 \qquad k^2|\vec{a}|^2-k\vec{a}\cdot \vec{b}=0$

$|\vec{a}|=4, \quad \vec{a}\cdot \vec{b}=6 \quad より \quad 16k^2-6k=0 \qquad k > 0 \quad だから \quad k=\cfrac{3}{8}$

$\therefore \ \ \vec{OF}=\cfrac{3}{8}\vec{a}$

(2)

　
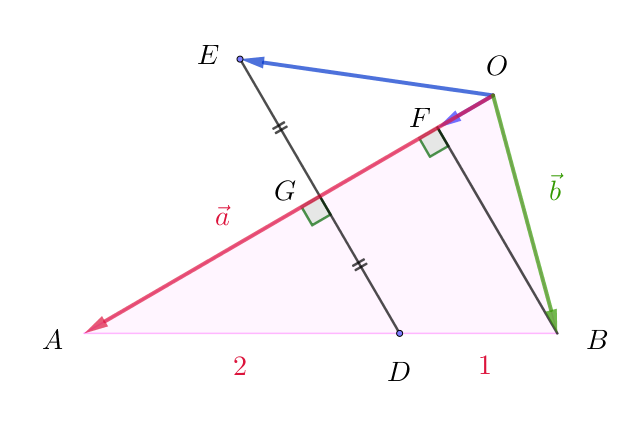
$\vec{BF}=\vec{OF}-\vec{OB}=\cfrac{3}{8}\vec{a} -\vec{b}$

$線分 \ DE\ と \ OA\ の交点を \ G\ とする。$

$DG /\!/ BF \ \ だから、 平行線の性質より \quad DG:BF=AD:AB=2:3$

$DG=\cfrac{2}{3}BF \qquad \vec{DG}=\cfrac{2}{3}\vec{BF}=\cfrac{2}{3}(\cfrac{3}{8}\vec{a} -\vec{b})=\cfrac{1}{4}\vec{a}-\cfrac{2}{3}\vec{b}$

$\therefore \ \ \vec{OE}=\vec{OD}+\vec{DE}=\vec{OD}+2\vec{DG}=\cfrac{\vec{a}+2\vec{b}}{3} + 2(\cfrac{1}{4}\vec{a}-\cfrac{2}{3}\vec{b})=\cfrac{5}{6}\vec{a} - \cfrac{2}{3}\vec{b}$

(3)

　
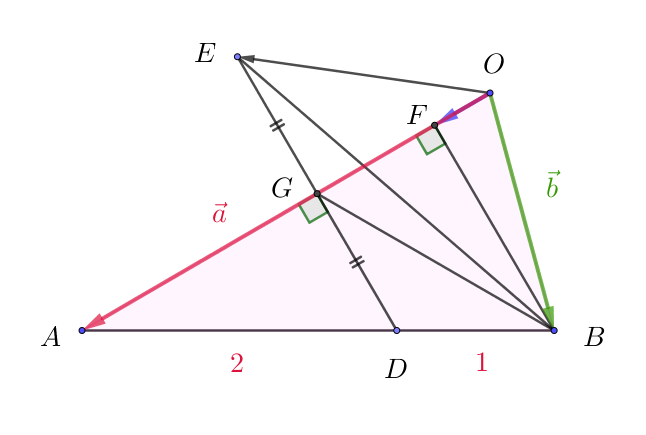
$\triangle BDG : \triangle BDE=DG : DE=1:2 \quad より$

$\quad \triangle BDG=\cfrac{1}{2} \triangle BDE=\cfrac{1}{2} \times \cfrac{5}{9}=\cfrac{5}{18}$

$\triangle ABG : \triangle BDG=AB : BD=3:1 \quad より$

$\quad \triangle ABG=3 \triangle BDG=3 \times \cfrac{5}{18} =\cfrac{5}{6}$

$OF=\cfrac{3}{8}OA=\cfrac{3}{8} \times 4=\cfrac{3}{2}$

$AF=OA-OF=4-\cfrac{3}{2}=\cfrac{5}{2}$

$AG:AF=AD:AB=2:3 \quad より \quad AG=\cfrac{2}{3}AF=\cfrac{2}{3} \times \cfrac{5}{2}=\cfrac{5}{3}$

$よって \quad \triangle OAB : \triangle GAB=OA : GA=4:\cfrac{5}{3}=12:5 \quad より \quad \triangle OAB=\cfrac{12}{5} \triangle GAB=\cfrac{12}{5} \times \cfrac{5}{6}=2$

$一方 \quad \triangle OAB=\cfrac{1}{2}OA\ OB\ \sin \theta =2OB\sin \theta \quad だから$

$\quad 2OB\sin \theta =2 \qquad \therefore \ \ OB\sin \theta=1$

$また \quad \vec{OA}\cdot\vec{OB}=6 \quad より \quad OA\ OB \cos \theta=6 \qquad \therefore OB\cos \theta=\cfrac{3}{2}$

$(OB\sin \theta)^2+(OB\cos \theta)^2=1+\cfrac{9}{4}$

$OB^2=\cfrac{13}{4} \qquad \therefore \ \ |\vec{b}|=OB=\cfrac{\sqrt{13}}{2}$


$(後半の別解)$

$(2)より \quad \vec{BF}=\cfrac{3}{8}\vec{a} -\vec{b} \quad だから$

$BF^2=\big|\cfrac{3}{8}\vec{a} -\vec{b}\big|^2=\cfrac{9}{64}|\vec{a}|^2 - \cfrac{3}{4}\vec{a}\cdot \vec{b} + |\vec{b}|^2=\cfrac{9}{64} \times 16 - \cfrac{3}{4} \times 6 + |\vec{b}|^2 =|\vec{b}|^2-\cfrac{9}{4}$

$\triangle OAB=\cfrac{1}{2} \times OA \times BF=2\sqrt{|\vec{b}|^2-\cfrac{9}{4}}$

$一方 \quad \triangle OAB=2 \quad だから \qquad |\vec{b}|^2-\cfrac{9}{4}=1 $

$|\vec{b}|^2=\cfrac{13}{4} \qquad \therefore \ \ |\vec{b}|=\cfrac{\sqrt{13}}{2}$

ページの先頭へ↑