広島大学(理系) 2024年 問題4
$複素数平面において、点\ 1\ を中心とする半径 \ \sqrt{2}\ の円を \ C\ とする。次の問いに答えよ。$
$(1)\ \ 点\ \alpha \ が円 \ C\ と虚軸との交点であるとき、\alpha + \cfrac{1}{\alpha}\ \ を求めよ。$
$(2)\ \ 円 \ C\ 上の点 \ z\ に対し、点 \ -\cfrac{1}{z}\ \ も円 \ C\ 上にあることを示せ。$
$(3)\ \ 円 \ C\ 上の点 \ z\ に対し、w=z+\cfrac{1}{z}\ \ とする。複素数 \ w,\ z\ は \ \ |w-2|=\cfrac{2}{|z|}\ \ を満たすことを示せ。$
$(4)\ \ 円 \ C\ 上の点 \ z\ に対し、(3)で定めた複素数 \ w\ は \ \ |w-2||w+2|=4 \ \ を満たすことを示せ。$
(1)
$点\ 1\ を中心とする半径 \ \sqrt{2}\ の円 \ C\ 上の点 \ z\ は、|z-1|=\sqrt{2} \ \ と表される。$
$点\ \alpha \ は円 \ C\ と虚軸との交点であるから、\alpha =bi \ \ (b\ は実数)\ \ とおける。$
$|bi-1|=\sqrt{2} \quad より \quad b^2+1=2 \qquad b=\pm 1$
$よって \quad \alpha =\pm i$
$このとき$
$\alpha + \cfrac{1}{\alpha}=\cfrac{\alpha ^2+1}{\alpha}=\cfrac{(\pm i)^2+1}{\alpha}=0$
$(別解)$
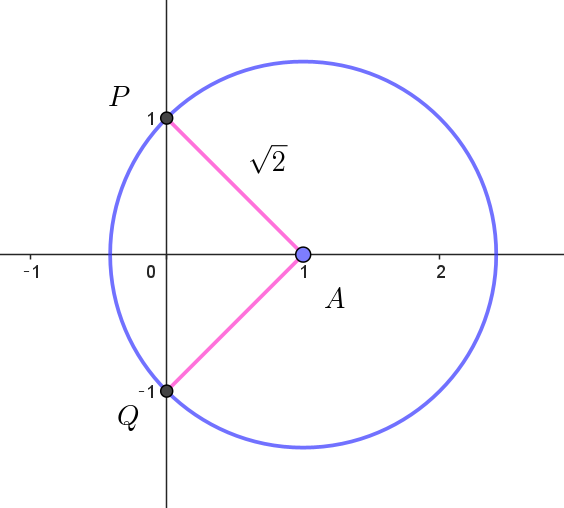
$円 \ C\ の中心を \ A,虚軸との交点を \ P,\ \ Q\ とすると$
$OP^2=AP^2-OA^2=2-1=1 \qquad OP=OQ=1$
$よって \quad P(i),\ \ Q(-i)\ \ だから、\alpha=\pm i$
(2)
$w=-\cfrac{1}{z} \quad とおくと \quad z=-\cfrac{1}{w}$
$|z-1|=\sqrt{2} \quad に代入して \quad \big|-\cfrac{1}{w}-1\big|=\sqrt{2}$
$\big|\cfrac{1}{w}+1\big|=\sqrt{2}$
$\big|\cfrac{w+1}{w}\big|=\sqrt{2}$
$|w+1|=\sqrt{2}|w|$
$両辺 \ 2\ 乗して$
$(w+1)(\overline{w+1})=2w\overline{w}$
$(w+1)(\overline{w}+1)=2w\overline{w}$
$w\overline{w}-w -\overline{w}=1$
$(w-1)(\overline{w}-1) =2$
$|w-1|^2=2$
$|w-1|=\sqrt{2}$
$よって \quad 円 \ C\ 上の点 \ z\ に対し、点 \ -\cfrac{1}{z}\ \ も円 \ C\ 上にある。$
(3)
\begin{eqnarray*} |w-2| &=&\big|z+\cfrac{1}{z}-2\big|\\ \\ &=&\big|\cfrac{z^2-2z+1}{z}\big|\\ \\ &=&\big|\cfrac{(z-1)^2}{z}\big|\\ \\ &=&\cfrac{|z-1|^2}{|z|}\\ \\ &=&\cfrac{2}{|z|} \end{eqnarray*}
(4)
\begin{eqnarray*} & &|w-2||w+2|\\ \\ &=&\cfrac{2}{|z|} \times \big|z+\cfrac{1}{z}+2\big|\\ \\ &=&\cfrac{2}{|z|} \times \big|\cfrac{(z+1)^2}{z}\big|\\ \\ &=&2\big|\cfrac{z+1}{z}\big|^2\\ \\ &=&2\big|1+\cfrac{1}{z}\big|^2\\ \end{eqnarray*}$(2)より点 \ -\cfrac{1}{z}\ \ も円 \ C\ 上にあるから \quad |-\cfrac{1}{z}-1|=\sqrt{2} \qquad \therefore \ \ |1+\cfrac{1}{z}|=\sqrt{2}$
$よって \quad |w-2||w+2|=2|1+\cfrac{1}{z}|^2=2 \times 2=4$
メインメニュー に戻る