広島大学(理系) 2024年 問題2
$座標空間内の\ 4\ 点O(0,\ 0,\ 0),\ A(1,\ 1,\ 0),\ B(0,\ 1,\ 1),\ C(1,\ 2,\ -1)\ に対し、\vec{OA}=\vec{a},\ \vec{OB}=\vec{b},\ \vec{OC}=\vec{c}\ \ とおく。$
$次の問いに答えよ。$
$(1)\ \ 内積 \ \ \vec{a} \cdot \vec{b},\ \ \vec{a} \cdot \vec{c},\ \ \vec{b} \cdot \vec{c} \ \ の値を求めよ。$
$(2)\ \ 点O,\ A,\ B\ を通る平面を \ \alpha \ とする。点 \ C\ から平面 \ \alpha \ に下ろした垂線と平面 \ \alpha \ の交点を \ M\ とする。$
$\quad 点 \ M\ の座標を求めよ。$
$(3)\ \ 点 \ M\ を(2)で定めた点とする。点 \ D\ を直線 \ CM\ 上の点であって \ \ |\vec{AC}|=|\vec{AD}| \ \ となるものとする。$
$\quad ただし、点 \ D\ は点 \ C\ とは異なる点である。このとき、点 \ D\ の座標を求めよ。$
$(4)\ \ 点 \ D\ を(2)で定めた点とする。三角形 \ CAD\ の面積 \ S\ を求めよ。$
(1)
$\vec{a} \cdot \vec{b}=(1,\ 1,\ 0)\cdot (0,\ 1,\ 1)=1 \times 0 + 1 \times 1+ 0 \times 1=1$
$\vec{a} \cdot \vec{c}=(1,\ 1,\ 0)\cdot (1,\ 2,\ -1)=1 \times 1 + 1 \times 2+ 0 \times (-1)=3$
$\vec{b} \cdot \vec{c}=(0,\ 1,\ 1)\cdot (1,\ 2,\ -1)=0 \times 1 + 1 \times 2+ 1 \times (-1)=1$
(2)
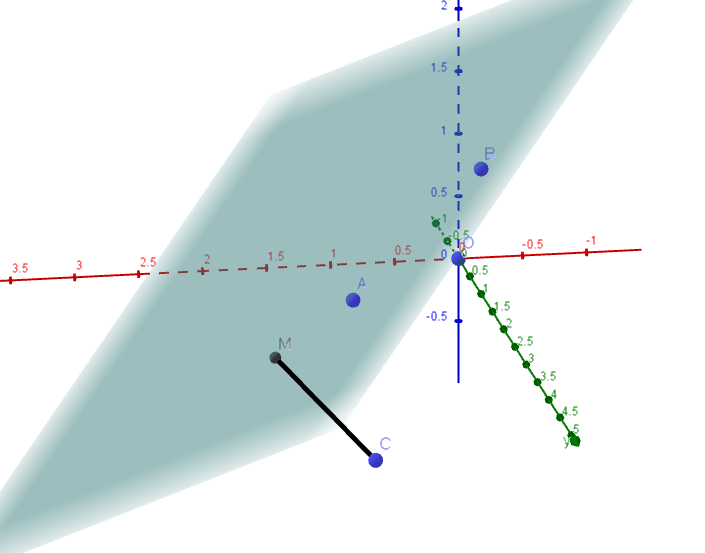
$点M\ は \ 3\ 点O,\ A,\ B\ を通る平面\ \alpha \ 上にあるから$
$\vec{OM}=p\vec{OA}+q\vec{OB}\ \ (p,\ q\ は実数)\ \ とおける。$
$\vec{OM}=p\vec{a}+q\vec{b}$
$CM \perp \alpha \ \ だから \ CM \ は \ \alpha \ 上の任意の直線と垂直である。$
(i)$\ \ \vec{CM} \perp \vec{OA} \quad より$
$ \quad (\vec{OM}-\vec{OC})\cdot \vec{OA}=0$
$ \quad (p\vec{a}+q\vec{b}-\vec{c}) \cdot \vec{a}=0$
$ \quad p|\vec{a}|^2 +q\vec{b}\cdot \vec{a}-\vec{c} \cdot \vec{a}=0$
$ \quad 2p+q-3=0 \hspace{5em}①$
(ii)$\ \ \vec{CM} \perp \vec{OB} \quad より$
$ \quad (\vec{OM}-\vec{OC})\cdot \vec{OB}=0$
$ \quad (p\vec{a}+q\vec{b}-\vec{c}) \cdot \vec{b}=0$
$ \quad p\vec{a}\cdot \vec{b} + q|\vec{b}|^2 -\vec{c} \cdot \vec{b}=0$
$ \quad p+2q-1=0 \hspace{5em}②$
$①②を解いて \quad p=\cfrac{5}{3}, \quad q=-\cfrac{1}{3}$
$\vec{OM}=\cfrac{5}{3}\vec{OA} -\cfrac{1}{3}\vec{OB}=\cfrac{5}{3}(1,\ 1,\ 0)-\cfrac{1}{3}(0,\ 1,\ 1)=(\cfrac{5}{3},\ \cfrac{4}{3},\ -\cfrac{1}{3})$
$よって \quad M(\cfrac{5}{3},\ \cfrac{4}{3},\ -\cfrac{1}{3})$
(3)
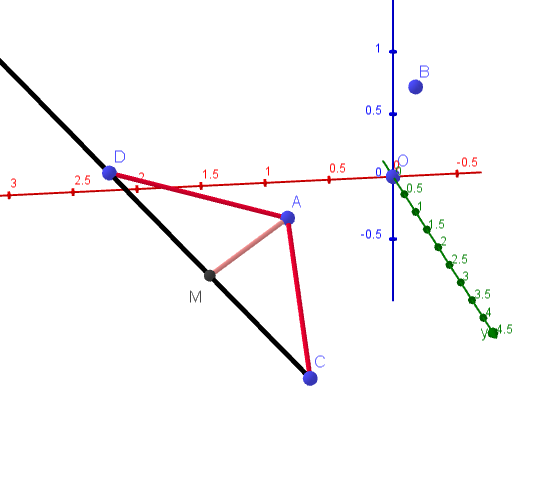
$CM \perp \alpha \ \ だから \ \ CM\ \ は平面 \ \alpha \ 上の任意の直線に垂直である。$
$\therefore \ \ CM \perp AM$
$|\vec{AC}|=|\vec{AD}| \ \ より \ \ \triangle ACD \ \ は二等辺三角形だから$
$M\ は \ CD\ の中点である。$
$\cfrac{1}{2}(\vec{OC}+\vec{OD})=\vec{OM}$
$\vec{OD}=2\vec{OM}-\vec{OC}=2(\cfrac{5}{3},\ \cfrac{4}{3},\ -\cfrac{1}{3})-(1,\ 2,\ -1)=(\cfrac{7}{3},\ \cfrac{2}{3},\ \cfrac{1}{3})$
$よって \quad D(\cfrac{7}{3},\ \cfrac{2}{3},\ \cfrac{1}{3})$
(4)
\begin{eqnarray*} S &=&\cfrac{1}{2} \times CD \times AM\\ \\ &=&\cfrac{1}{2} \times 2CM \times AM\\ \\ &=&\sqrt{(\cfrac{5}{3}-1)^2+(\cfrac{4}{3}-2)^2+(-\cfrac{1}{3}+1)^2} \times \sqrt{(\cfrac{5}{3}-1)^2+(\cfrac{4}{3}-1)^2+(-\cfrac{1}{3}-0)^2}\\ \\ &=&\sqrt{\cfrac{4}{3}} \times \sqrt{\cfrac{2}{3}}\\ \\ &=&\cfrac{2\sqrt{2}}{3} \end{eqnarray*}
メインメニュー に戻る