広島大学(理系) 2023年　問題5


$関数 \ \ f(x)=\log \cfrac{3x+3}{x^2+3}\ \ について、次の問いに答えよ。$
$(1)\ \ y=f(x)\ のグラフの概形をかけ。ただし、グラフの凹凸は調べなくてよい。$
$(2)\ \ s\ を定数とするとき、次の \ x\ についての方程式(*)の異なる実数解の個数を調べよ。$
$ \hspace{10em} (*) \quad f(x)=s$
\[(3)\ \ 定積分 \ \ \int_0^3 \cfrac{2x^2}{x^2+3} dx \ \ の値を求めよ。\] $(4)\ \ (2)の(*)が実数解をもつ \ s\ に対して、(2)の(*)の実数解のうち最大のものから最小のものを$
$\quad 引いた差を \ g(s)\ とする。ただし、(2)の(*)の実数解が一つだけであるときには \ g(s)=0\ とする。$
\[\quad 関数 \ f(x)\ の最大値を \ \alpha \ とおくとき、定積分 \ \ \int _0^{\alpha}g(s)ds \ \ の値を求めよ。\]


(1)


$y=\log3+\log(x+1)-\log(x^2+3) \quad だから$
\begin{eqnarray*} y' &=&\cfrac{1}{x+1}-\cfrac{2x}{x^2+3}\\ \\ &=&\cfrac{(x^2+3)-2x(x+1)}{(x+1)(x^2+3)}\\ \\ &=&\cfrac{-(x^2+2x-3)}{(x+1)(x^2+3)}\\ \\ &=&-\cfrac{(x+3)(x-1)}{(x+1)(x^2+3)} \end{eqnarray*}
$x > -1 \quad だから \quad y'=0 \quad より \quad x=1$

\[増減表は \qquad \begin{array}{c||c|c|c|c|c} x & -1 & \cdots & 1 & \cdots \\ \hline y' & & + & 0 & - & \\ \hline y & & \nearrow & 極大 & \searrow & \\ \end{array} \]

　

$x=1 \ \ で極大となり、極大値 \ \ y=\log \cfrac{6}{4}=\log \cfrac{3}{2}$

$f(x)=0 \ \ より \ \ \cfrac{3x+3}{x^2+3}=1 \qquad 3x+3=x^2+3 \qquad \therefore \ \ x=0,\ \ 3$

$x \longrightarrow -1+0 \quad のとき \quad 　y \longrightarrow -\infty$

$x \longrightarrow +\infty \quad のとき \quad 　y \longrightarrow -\infty$

$よって グラフの概形は右図のとおり$


(2)


$方程式 \ \ f(x)=s \ \ の異なる実数解の個数は、曲線 \ \ y=f(x)\ \ と$

$直線 \ \ x=s \ \ との共有点の個数だから$

　

(i)$\ \ s < \log\cfrac{3}{2} \quad のとき \quad 2\ 個$

(ii)$\ \ s = \log\cfrac{3}{2} \quad のとき \quad 1\ 個$

(iii)$\ \ s > \log\cfrac{3}{2} \quad のとき \quad 0\ 個$


(3)


\begin{eqnarray*} I &=&\int_0^3 \cfrac{2x^2}{x^2+3} dx\\ \\ &=&\int_0^3 \big(2-\cfrac{6}{x^2+3}\big) dx\\ \\ &=&\int_0^3 2dx - 6\int_0^3 \cfrac{1}{x^2+3}dx\\ \end{eqnarray*} \[第2項\ \ J=\int_0^3 \cfrac{1}{x^2+3}dx \quad において \quad x=\sqrt{3}\tan \theta \quad とおくと \qquad dx=\cfrac{\sqrt{3}}{\cos ^2\theta} d\theta \qquad \begin{array}{c|c} x & 0\ \ \rightarrow 3 \\ \hline \theta & 0 \rightarrow \cfrac{\pi}{3}\\ \end{array} \]
\begin{eqnarray*} J &=&\int_0^{\scriptsize{\cfrac{\pi}{3}}} \cfrac{1}{3\tan ^2 \theta +3} \cdot \cfrac{\sqrt{3}}{\cos ^2\theta} d\theta\\ \\ &=&\cfrac{\sqrt{3}}{3}\int_0^{\scriptsize{\cfrac{\pi}{3}}} \cfrac{1}{\tan ^2 \theta +1} \cdot \cfrac{1}{\cos ^2\theta}d\theta\\ \\ &=&\cfrac{\sqrt{3}}{3}\int_0^{\scriptsize{\cfrac{\pi}{3}}}d\theta\\ \\ &=&\cfrac{\sqrt{3}}{9}\pi \end{eqnarray*} $よって \quad I=6 -6 \times \cfrac{\sqrt{3}}{9}\pi=6-\cfrac{2\sqrt{3}}{3}\pi$


(4)

　

$g(s)ds \ \ は右図のように \ \ y=f(x)\ \ を \ y\ 軸に垂直に \ y=s\ と \ y=s+ds \ で$

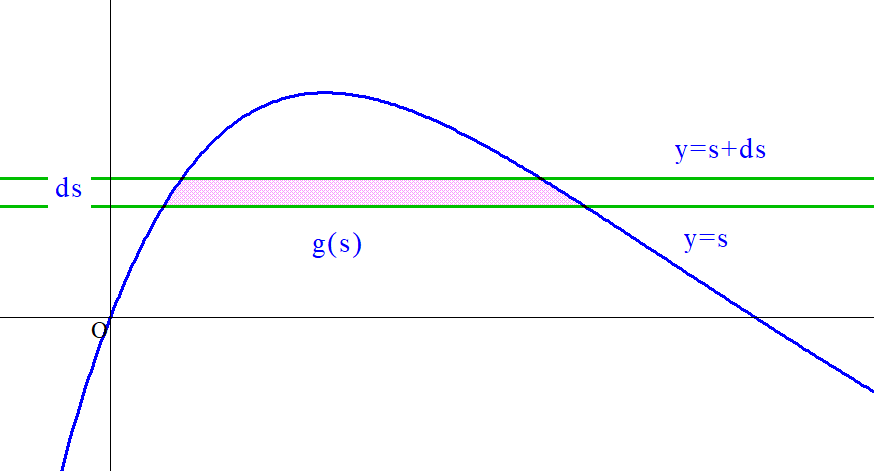
$切ったときの微小長方形の面積であるから$
\[S=\int _0^{\alpha}g(s)ds \ \ は \ y=f(x)\ と \ x\ 軸で囲まれた領域の面積に等しい。\]

　

$よって$
\begin{eqnarray*} S &=&\int_0^3 f(x)dx\\ \\ &=&\int_0^3 \big(\log(3x+3)-\log(x^2+3)\big)dx\\ \\ &=&\int_0^3 \big(\log 3+\log (x+1)-\log(x^2+3)\big)dx\\ \end{eqnarray*}
\begin{eqnarray*} 第2項 &=&\int_0^3 \log(x+1)dx\\ \\ &=&\big[(x+1)\log(x+1)\big]_0^3 - \int_0^3 (x+1) \times \cfrac{1}{x+1}dx\\ \\ &=&4\log 4-\int_0^3dx\\ \\ &=&8\log 2-3 \end{eqnarray*}
\begin{eqnarray*} 第3項 &=&\int_0^3 \log(x^2+3)dx\\ \\ &=&\big[x\log(x^2+3)\big]_0^3 - \int_0^3 x \times \cfrac{2x}{x^2+3}dx\\ \\ &=&3\log 12-\int_0^3 \cfrac{2x^2}{x^2+3}dx \hspace{5em} ((3)より)\\ \\ &=& 3\log (2^2 \times 3) - (6-\cfrac{2\sqrt{3}}{3}\pi)\\ \\ &=&6\log 2+3\log 3 -6+ \cfrac{2\sqrt{3}}{3}\pi \end{eqnarray*}
$よって求める定積分の値は$
\begin{eqnarray*} \quad S &=&3\log 3 +(8\log 2-3) -(6\log 2+3\log 3 -6+ \cfrac{2\sqrt{3}}{3}\pi)\\ \\ &=&3+2\log 2 -\cfrac{2\sqrt{3}}{3}\pi \end{eqnarray*}

ページの先頭へ↑



メインメニュー　に戻る