広島大学(理系) 2023年　問題3


$空間内の \ 6\ 点 \ A,\ B,\ C,\ D,\ E,\ F\ は \ 1\ 辺の長さが \ 1\ の正八面体の頂点であり、四角形 \ ABCD\ は正方形で$
$あるとする。\vec{b}=\vec{AB},\ \vec{d}=\vec{AD},\ \vec{e}=\vec{AE}\ とおくとき、次の問いに答えよ。$
$(1)\ \ 内積 \ \vec{b}\cdot \vec{d}, \ \ \vec{b}\cdot \vec{e},\ \ \vec{d}\cdot \vec{e} \ \ の値を求めよ。$
$(2)\ \ \vec{AF}=p\vec{b}+q\vec{d}+r\vec{e}\ \ を満たす実数 \ p,\ q,\ r\ の値を求めよ。$
$(3)\ \ 辺 \ BE\ を \ 1:2\ に内分する点を \ G\ とする。また、0 < t < 1\ を満たす実数 \ t\ に対し、辺 \ CF\ を$
$\quad \ t:(1-t)\ に内分する点を \ H\ とする。t\ が \ 0 < t < 1\ の範囲を動くとき、\triangle AGH \ の面積が最小と$
$\quad なる \ t\ の値とそのときの \ \triangle AGH \ の面積を求めよ。$


(1)

　

$四角形 \ ABCD\ は正方形だから \ \ AB \perp AD \ \ より \ \ \vec{b}\cdot \vec{d}=0$

$\triangle ABE \ \ と \ \ \triangle ADE\ \ は \ 1\ 辺 \ 1\ の正三角形だから$

$\vec{b}\cdot \vec{e}=1 \times 1 \times \cos \cfrac{\pi}{3}=\cfrac{1}{2},\qquad \vec{d}\cdot \vec{e}=1 \times 1 \times \cos \cfrac{\pi}{3}=\cfrac{1}{2}$


(2)


$正方形 \ ABCD\ の対角線 \ AC\ と \ BD\ の交点を \ O\ とする。$

$\vec{OE}=\vec{AE}-\vec{AO}=\vec{AE}-\cfrac{1}{2}(\vec{AB}+\vec{AD})=\vec{e}-\cfrac{1}{2}(\vec{b}+\vec{d})$

$\vec{AF}=\vec{AO}+\vec{OF}=\vec{AO}-\vec{OE}=\cfrac{1}{2}(\vec{b}+\vec{d})-\big(\vec{e}-\cfrac{1}{2}(\vec{b}+\vec{d})\big)=\vec{b}+\vec{d}-\vec{e} $

$\vec{AF}=p\vec{b}+q\vec{d}+r\vec{e}=\vec{b}+\vec{d}-\vec{e} \ \ より$

$\vec{b}, \ \ \vec{d},\ \ \vec{e}\ \ は互いに平行でない(一次独立)から \quad p=1,\ \ q=1,\ \ r=-1$


(3)

　

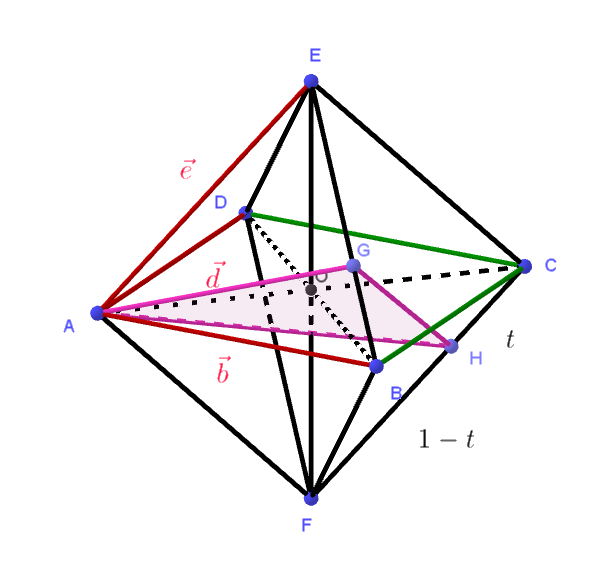
$\vec{AG}=\cfrac{2\vec{b}+\vec{e}}{1+2}=\cfrac{1}{3}(2\vec{b}+\vec{e})$

$\vec{AH}=(1-t)\vec{AC}+t\vec{AF}=(1-t)(\vec{b}+\vec{d}) +t(\vec{b}+\vec{d}-\vec{e})=\vec{b}+\vec{d}-t\vec{e} $

\begin{eqnarray*} \triangle AGH &=&\cfrac{1}{2}AG \cdot AH \cdot \sin \angle GAH\\ \\ &=&\cfrac{1}{2}AG \cdot AH \cdot \sqrt{1-\cos ^2 \angle GAH}\\ \\ &=&\cfrac{1}{2} \sqrt{AG^2 \cdot AH^2- (AG \cdot AH \cdot \cos \angle GAH)^2}\\ \\ &=&\cfrac{1}{2} \sqrt{AG^2 \cdot AH^2- (\vec{AG} \cdot \vec{AH})^2}\\ \end{eqnarray*}
$ここで$

$AG^2=|\vec{AG}|^2=\big|\cfrac{1}{3}(2\vec{b}+\vec{e})|^2=\cfrac{1}{9}(4|\vec{b}|^2+|\vec{e})|^2+4\vec{b} \cdot \vec{e})=\cfrac{1}{9}(4 \times 1^2+ 1^2 +4 \times \cfrac{1}{2})=\cfrac{7}{9}$

$AH^2=|\vec{b}+\vec{d}-t\vec{e}|^2=|\vec{b}|^2+|\vec{d}|^2+t^2|\vec{e}|^2+2\vec{b} \cdot \vec{d} - 2t\vec{d} \cdot \vec{e}-2t\vec{b} \cdot \vec{e}=1^2+1^2+t^2 -2t \times \cfrac{1}{2} -2t \times \cfrac{1}{2}=t^2-2t+2$

$\vec{AG} \cdot \vec{AH}=\cfrac{1}{3}(2\vec{b}+\vec{e}) \cdot (\vec{b}+\vec{d}-t\vec{e})=\cfrac{1}{3}(2|\vec{b}|^2+2\vec{b} \cdot \vec{d}-2t\vec{b}\cdot \vec{e}+ \vec{b} \cdot \vec{e}+\vec{d} \cdot \vec{e} -t|\vec{e}|^2)=\cfrac{1}{3}(3-2t)$

$よって$

$AG^2 \cdot AH^2- (\vec{AG} \cdot \vec{AH})^2=\cfrac{7}{9} \times (t^2-2t+2) - \cfrac{1}{9}(3-2t)^2=\cfrac{1}{9}(3t^2-2t+5)=\cfrac{1}{3}(t-\cfrac{1}{3})^2+\cfrac{14}{27}$

$\triangle AGH \ \ は \ \ t=\cfrac{1}{3}\ \ のとき最小で、最小値は \ \ \cfrac{1}{2} \times \sqrt{\cfrac{14}{27}}=\cfrac{\sqrt{42}}{18}$


ページの先頭へ↑




メインメニュー　に戻る