広島大学(理系) 2022年 問題2
$a\ を正の実数、t\ を \ 0 < t < 1\ を満たす実数とする。座標平面上の \ 3\ 点 \ A(0,\ a),\ B(-1,\ 0),\ C(1,\ 0) を頂点と$
$する二等辺三角形の内接円を \ S\ とし、その中心が \ I(0,\ t)\ であるとする。このとき、次の問いに答えよ。$
$(1)\ \ \angle IBC \ を \ \theta \ とおく。t\ と \ a\ を、それぞれ \ \theta \ を用いて表せ。$
$(2)\ \ a\ を \ t\ を用いて表せ。$
$(3)\ \ \triangle ABC \ の重心が内接円 \ S\ の周上にあるとき、t\ の値を求めよ。$
$(4)\ \ \triangle ABC \ の垂心が \ S\ の周上にあるとき、t\ の値を求めよ。ただし、三角形の各頂点から対辺、またはその$
$\quad 延長に下ろした \ 3\ 本の垂線は \ 1\ 点で交わることが知られており、その交わる点を三角形の垂線と呼ぶ。$
$(5)\ \ \triangle ABC \ の外心が \ S\ の周上にあるとき、t\ のとり得る値をすべて求めよ。$
$(解説)$
$(1)\ \ 内心は三角形の \ 3\ つの頂角の二等分線の交点です。$
$(2)\ \ 2\ 倍角の公式をつかいます。$
$(3)\ \ 重心は \ 3\ つの中線の交点だから、y\ 軸上にあります。$
$(4)\ \ 点 \ B\ を通り、辺 \ AC\ に垂直な直線求めます。垂心は \ y\ 軸上にありますので、x=0\ とおけば$
$\quad \ H\ の \ y\ 座標が求まります。$
$(5)\ \ 辺 \ AC\ の中点を通り、辺 \ AC\ に垂直な直線求めます。外心は \ y\ 軸上にありますが、S\ の上部と$
$\quad 下部(原点)の \ 2\ つあります。$
$\quad (参考)\ \ 三角形の \ 5\ 心については($三角形の5心$)をご覧ください。$
(1)

$点 \ I\ は \ \triangle ABC \ の内心だから、I\ は\angle B \ の二等分線上にある。$
$よって \quad \angle ABI=\angle IBC=\theta \quad より \quad \angle B=2\theta $
$直角三角形 \ OAB\ \ において \quad OA=OB\tan 2\theta =\tan 2\theta \quad \therefore \ \ a=\tan 2\theta$
$直角三角形 \ OIB\ \ において \quad OI=OB\tan \theta =\tan \theta \quad \therefore \ \ t=\tan \theta$
(2)
$\tan 2\theta=\cfrac{2\tan \theta}{1-\tan ^2\theta} \quad より \quad a=\cfrac{2t}{1-t^2}$
(3)

$\triangle ABC \ の重心 \ G\ は \ 3\ つの辺の中線の交点だから、y\ 軸上にある。$
$また、G(0,\ \cfrac{a}{3})\ \ で \ a > 0 \ \ だから \ G\ の \ y\ 座標は正である。$
$内接円の半径は \ t\ で、G\ が \ S\ 上にあるから \quad \cfrac{a}{3}=2t \quad \therefore \ \ a=6t$
$(2)より \quad a=\cfrac{2t}{1-t^2} \quad だから \quad 6t=\cfrac{2t}{1-t^2}$
$t > 0 \quad だから 両辺を \ 2t\ で割って整理すると$
$3(1-t^2)=1 \qquad t^2=\cfrac{2}{3} \qquad \therefore \ \ t=\cfrac{\sqrt{6}}{3}$
(4)
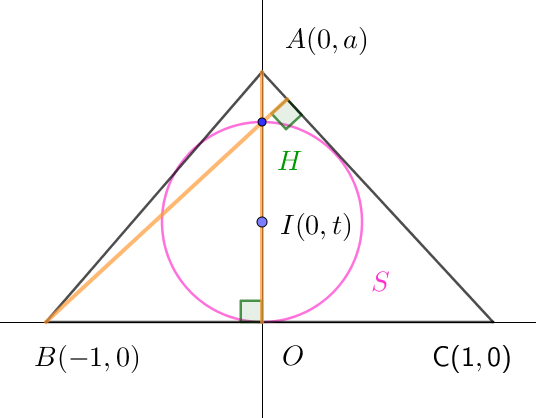
$\triangle ABC \ の垂心 \ H\ は \ 3\ つの頂点からそれぞれの対辺に下ろした垂線の$
$交点だから、y\ 軸上にある。$
$直線 \ AC\ の方程式は \quad y=-a(x-1)$
$これに垂直な直線 \ BH\ の方程式は \quad y=\cfrac{1}{a}(x+1)$
$y\ 軸との交点は \quad y=\cfrac{1}{a}$
$H\ が \ S\ 上にあるから \quad \cfrac{1}{a}=2t \quad \therefore \ \ a=\cfrac{1}{2t}$
$(2)より \quad a=\cfrac{2t}{1-t^2} \quad だから \quad \cfrac{1}{2t}=\cfrac{2t}{1-t^2}$
$分母を払って整理すると \quad t^2=\cfrac{1}{5} \qquad \therefore \ \ t=\cfrac{1}{\sqrt{5}}$
(5)
$線分 \ AC\ の中点 \ P\ は \ (\cfrac{1}{2},\ \cfrac{a}{2})\ \ だから垂直二等分線は \quad y=\cfrac{1}{a}(x-\cfrac{1}{2})+\cfrac{a}{2}$
$外心は \ y\ 軸との交点だから \ \ x=0 \ \ とおいて \quad y=-\cfrac{1}{2a}+\cfrac{a}{2}$
$この点が\ S\ の周上にあるのは次の \ 2\ 通りがある。$

(i)$\ \ 外心が内接円の上部にある場合$
$\quad -\cfrac{1}{2a}+\cfrac{a}{2}=2t \quad で(2)より \quad a=\cfrac{2t}{1-t^2} \quad だから $
$\quad -\cfrac{1-t^2}{4t}+\cfrac{t}{1-t^2}=2t \quad 分母を払って整理すると \quad 7t^4-2t^2-1=0$
$\quad t^2=\cfrac{1+2\sqrt{2}}{7} \qquad \therefore t=\cfrac{\sqrt{7(1+2\sqrt{2})}}{7}$

(ii)$\ \ 外心が内接円の下部(原点)にある場合$
$\quad -\cfrac{1}{2a}+\cfrac{a}{2}=0 \qquad a=\cfrac{1}{a} \qquad \therefore \ \ a=1$
$\quad a=\cfrac{2t}{1-t^2} \quad だから \quad \cfrac{1-t^2}{2t}=1 \quad 分母を払って整理すると$
$\quad t^2+2t-1=0 \qquad \therefore \ \ t=\sqrt{2}-1$
メインメニュー に戻る