広島大学(理系) 2021年 問題3
$1\ 個のさいころを \ 3\ 回投げる。1\ 回目に出た目の数を \ a、2\ 回目に出た目の数を \ b、3\ 回目に出た目の数を$
$c\ とする。また、f(x)=(-1)^ax^2+bx+c \ \ とする。次の問いに答えよ。$
$(1)\ \ b^2 > 4c \ \ である確率を求めよ。$
$(2)\ \ 2次方程式 \ \ f(x)=0 \ \ が異なる二つの実数解をもつ確率を求めよ。$
$(3)\ \ 2次方程式 \ \ f(x)=0 \ \ が異なる二つの実数解をもつとき、f'(1)=7 \ \ である条件付き確率を求めよ。$
$(4)\ \ 2次方程式 \ \ f(x)=0 \ \ が異なる二つの実数解をもつとき、少なくとも \ 1\ つが正の解である条件付き$
$\qquad 確率を求めよ。$
$(解説)$
$(1)\ \ b\ によって場合分けすればよいでしょう。$
$(2)\ \ 判別式が正であればよいのですが、(-1)^a \ \ の処理をどうするかです。$
$(3)\ \ 条件付き確率は表をかくと分かり易いです。$
$(4)\ \ 少なくと一つが正の解の余事象を考えた方が楽です。$
(1)
$b^2 >4c \ \ となる事象を \ B\ とする。$
$b^2 >4c \geqq 4 \quad だから \quad b^2 > 4$
(i)$\ \ b=3 \quad のとき \quad 4c < 9 \quad より \quad c=1,\ 2$
(ii)$\ \ b=4 \quad のとき \quad 4c < 16 \quad より \quad c=1,\ 2,\ 3$
(iii)$\ \ b=5 \quad のとき \quad 4c < 25 \quad より \quad c=1 ~ 6$
(iv)$\ \ b=6 \quad のとき \quad 4c < 36 \quad より \quad c=1 ~ 6$
$n(B)=2+3+6+6=17 \quad だから、求める確率 \ \ P(B)=\cfrac{17}{6 \times 6}=\cfrac{17}{36}$
(2)
$1\ 回目に出た目の数 \ a\ が \ 1,\ 3,\ 5\ である事象を \ A\ とすると、2,\ 4,\ 6\ である事象は \ \overline{A}\ である。$
$2\ 次方程式 \ \ f(x)=0 \ \ が異なる二つの実数解をもつ事象を \ C\ とする。$
$条件は判別式が \ \ D=b^2-4(-1)^a c> 0 \ \ である。$
(i)$\ \ a=1,\ 3,\ 5 \quad のとき、すなわち事象 \ A\ が起こったとき$
$\qquad D=b^2+4c > 0 \ \ だから \ 2,\ 3\ 回目に出た目の数 \ b,\ c\ によらず異なる二つの実数解をもつ。$
(ii)$\ \ a=2,\ 4,\ 6 \quad のとき、すなわち事象 \ \overline{A}\ が起こったとき$
$\qquad D=b^2-4c >0 \ \ となるのは(1)で事象 \ B\ が起こったことと同じである。$
(i),(ii)$\ \ より求める確率 \ P(C)\ は$
\begin{eqnarray*} P(C) &=&P(A \cap C)+P(\overline{A} \cap C)\\ \\ &=&P(A)P_A(C)+P(\overline{A}) P_{\overline{A}}(C)\\ \\ &=&\cfrac{1}{2}\times 1 + \cfrac{1}{2} \times \cfrac{17}{36}\\ \\ &=&\cfrac{53}{72}\\ \end{eqnarray*}
$(別解)$
$さいころを \ 3\ 回投げたときの根元事象を考えると$
$\qquad n(U)=6^3 ,\qquad n(A \cap C)=3 \times 6^2,\qquad n(\overline{A} \cap C)=3 \times 17$
$よって \quad P(C)=\cfrac{3 \times 6^2}{6^3}+\cfrac{3 \times 17}{6^3}=\cfrac{53}{72}$
(3)
$f'(1)=7 \ \ である事象を \ E\ とする。$
$\quad f'(x)=2(-1)^ax+b \quad より \quad f'(1)=2(-1)^a+b=7 \qquad b=7-2(-1)^a$
(i)$\ \ a=1,\ 3,\ 5 \quad のとき、すなわち事象 \ A\ が起こったとき$
$\qquad b=7+2=9 \quad となり、これは空事象である。$
(ii)$\ \ a=2,\ 4,\ 6 \quad のとき、すなわち事象 \ \overline{A}\ が起こったとき$
$\qquad b=7-2=5$
$満たす根元事象は、右図の$○$の部分である。$
$\hspace{40em}\overline{A}=\{2,4,6\}$
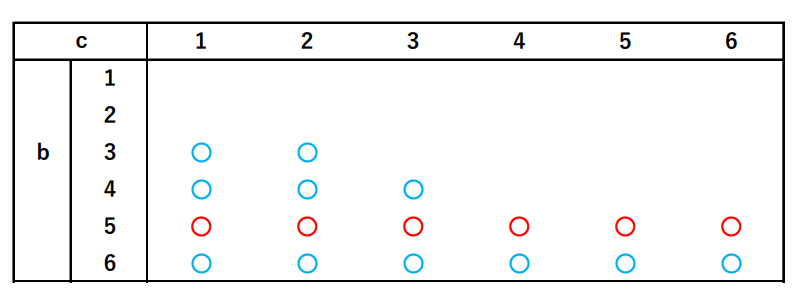
$P(C \cap E)=\cfrac{3 \times 6}{6^3}=\cfrac{1}{12}$
$P_C(E)=\cfrac{P(C \cap E)}{P(C)}=\cfrac{1}{12} \times \cfrac{72}{53}=\cfrac{6}{53}$
(4)
$少なくとも \ 1\ つが正の解である事象を \ F\ とすると、余事象\overline{F}\ は、2\ つとも負の解である。$
$\quad \alpha < 0,\quad \beta < 0 \Longleftrightarrow \alpha +\beta < 0 ,\quad \alpha \beta >0$
$\qquad \alpha +\beta =-\cfrac{b}{(-1)^a} < 0 \quad より \quad (-1)^a b > 0$
$\qquad \alpha \beta =\cfrac{c}{(-1)^a} > 0 \quad より \quad (-1)^a c > 0$
(i)$\ \ a=1,\ 3,\ 5 \quad のとき、すなわち事象 \ A\ が起こったとき$
$\qquad (-1)^a =-1 \quad だから \quad b < 0,\quad c < 0 \quad となり、これは空事象である。$
(ii)$\ \ a=2,\ 4,\ 6 \quad のとき、すなわち事象 \ \overline{A}\ が起こったとき$
$\qquad (-1)^a =1 \quad だから \quad b > 0, \quad c > 0 \quad となる。$
$満たす根元事象は、右図の$○$の部分である。$
$\hspace{40em}\overline{A}=\{2,4,6\}$
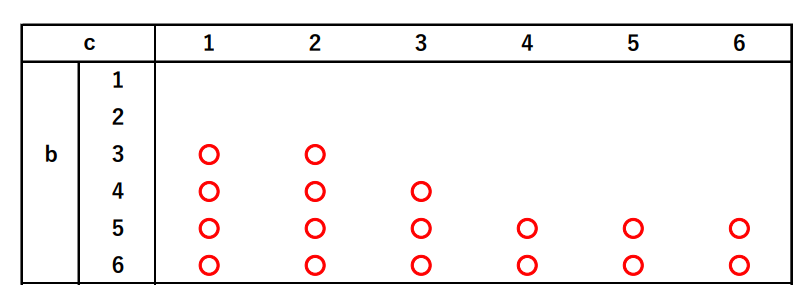
$P(C \cap \overline{F})=\cfrac{3 \times 17}{6^3}=\cfrac{17}{72}$
$P_C(\overline{F})=\cfrac{P(C \cap \overline{F})}{P(C)}=\cfrac{17}{72} \times \cfrac{72}{53}=\cfrac{17}{53}$
$よって求める確率は \quad P_C(F)=1-P_C(\overline{F})=1- \cfrac{17}{53}=\cfrac{36}{53}$
メインメニュー に戻る