広島大学(理系)2017年前期 問題5
$x$座標,$y$座標がともに整数である座標平面上の点を格子点とよぶ。
格子点$O(0,0)$および$A(50,14)$を考える。次の問いに答えよ。
$(1) \quad \vec{OP}・\vec{OA}=6 を満たす格子点Pを1つ求めよ。$
$(2) \quad mを自然数とする。 \vec{OP}・\vec{OA}=6 を満たす格子点Pのうち、長さOPがm番目に$
$\hspace{2em} 小さい点を P_mとする。P_1\ および\ P_2を求めよ。$
$(3) \quad P_mを(2)で求めた格子点とする。自然数kに対し、ベクトル\vec{P_{2k}P_{2k+1}}および \vec{P_{2k}P_{2k+2}}$
を成分表示せよ。
$(4) \quad P_mを(2)で求めた格子点とする。Qを\vec{OQ}=\vec{P_{14}P_{16}}を満たす点とする。$
$\hspace{2em}$ 四角形$OQP_{16}P_{14}$の周および内部に含まれる格子点をすべて求めよ。
(1)は不定方程式を解くだけです。
(2)は点$P$が直線上に並ぶことがわかれば解けます。
(3)はベクトルの成分表示の計算です。
(4)が、出題者が出したかった本音の問題です。格子点を効率よく、正確に調べ上げるにはどう
すればよいかです。当然まともにぶつかったら時間ばかりかかってしまいます。
そこで、私なりの方法を考えましたので、紹介します。
(1)
$P(x,y)とおくと、\vec{OA}=(50,14),\quad \vec{OP}=(x,y)$$\vec{OP}・ \vec{OA} = 6 より 50x+14y=6 \qquad 25x+7y=3 \hspace{6em}$ (1)
$25x+7y=1$ の整数解は $x=2,\quad y=-7$ であるから
$25×2+7×(-7)=1$
両辺を$3$倍して $25×6+7×(-21)=3 \hspace{12em}$ (2)
(1)$\ $- $\ $(2) より
$25(x-6)+7(y+21)=0$
$25と7は互いに素だから、n$を整数として
$x-6=7n,\quad y+21=-25n$ とおける。
したがって $x=6+7n,\quad y=-21-25n$
$n=-1$ とおくと $x=-1,\quad y=4 よって P(-1,4)$
(2)
(1)より $x=6+7n,\quad y=-21-25n$ の$n$に順次代入して点$P$の座標を求めると$\hspace{3em} \vdots$
$\qquad n=-3 のとき P(-15,54)$
$\qquad n=-2 のとき P(-8,29)$
$\qquad n=-1 のとき P(-1,4)$
$\qquad n=0 \quad のとき P(6,-21)$
$\qquad n=1 \quad のとき P(13,-46)$
$\qquad n=2 \quad のとき P(20,-71)$
$\hspace{3em} \vdots$
$n$を消去すると
$25(x-6)+7(y+21)=0$
$y+21=-\cfrac{25}{7}(x-6)$
したがって 点$Pは点(6,-21)を通り、傾き-\cfrac{25}{7}$ の直線上にある。
$\hspace{6em}$
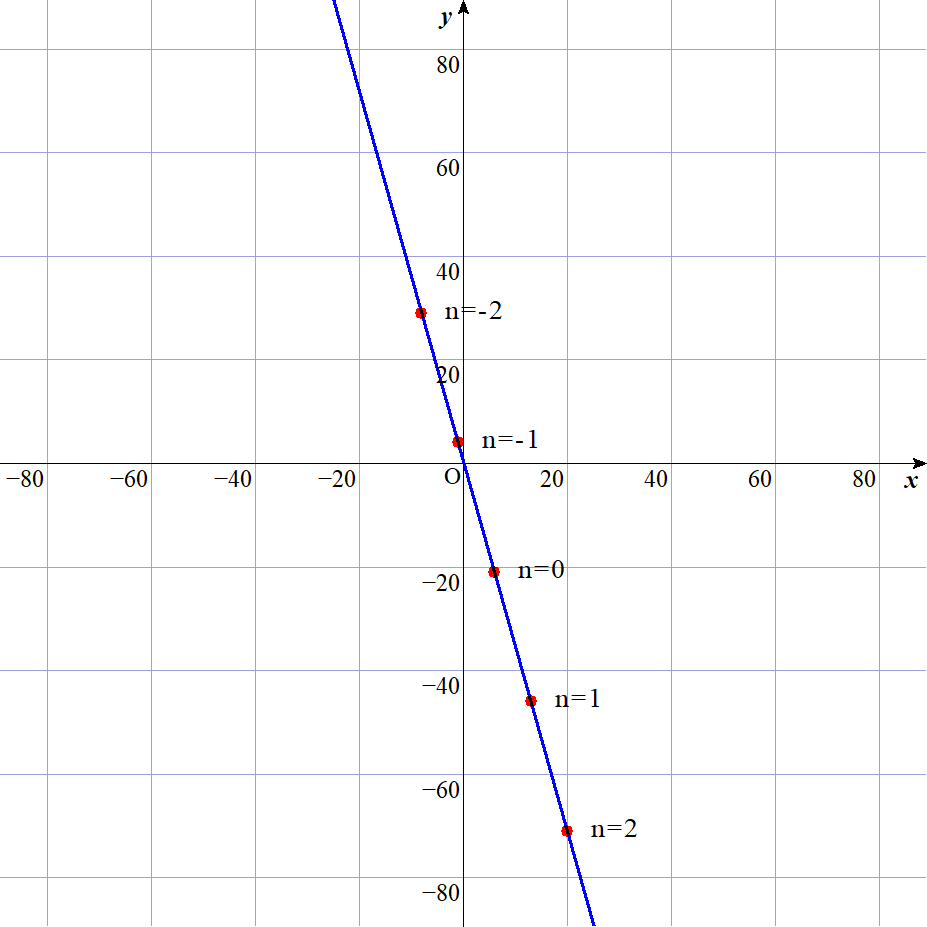
これより$OP$が
$1$番小さい点 $\quad P_1$ は $n=-1 のときで P_1(-1,4)$
$2$番目に小さい点 $P_2$ は $n=0 のときで \quad P_2(6,-21)$
であることがわかる。
(3)
長さ$OPの大小は点 P のx 座標とy座標の絶対値の和 |6+7n|+|-21-25n|$ の大小に一致することに注意して
点$P_m \ (m=1,2,3, \cdots)をとるnは -1,0,-2,1,-3,2, \cdots$ である。
このままでは$mとn$の関係が見にくいので
$n+1=p とするとpは順に 0,1,-1,2,-2,3,\cdot$ となって見通しがよくなる。
$x,y をpで表すと x=6+7(p-1)=-1+7p,\quad y=-21-25(p-1)=4-25p$
したがって
$m=2k \quad のときは \quad p=k \quad で \quad P_{2k}(-1+7k,4-25k)$
$m=2k+1 \quad のときは \quad p=-k \quad で \quad P_{2k+1}(-1-7k,4+25k)$
よって
$\vec{P_{2k}P_{2k+1}}=\vec{OP_{2k+1}}-\vec{OP_{2k}}$
$\hspace{4em} =(-1-7k,4+25k)-(-1+7k,4-25k)$
$\hspace{4em} =(-14k,50k)$
$\vec{P_{2k}P_{2k+2}}=\vec{OP_{2k+2}}-\vec{OP_{2k}}$
$\hspace{4em} =(-1+7(k+1),4-25(k+1))-(-1+7k,4-25k)$
$\hspace{4em} =(7,-25)$
(4)
(3)より $\vec{OQ}=\vec{P_{14}P_{16}}=(7,-25) \qquad \therefore Q(7,-25)$
点$P_{14}はk=7 のときだから P_{14}(48,-171)$
点$P_{16}はk=8 のときだから P_{16}(55,-196)$
$\vec{OQ}=\vec{P_{14}P_{16}}$だから四角形$OQP_{16}P_{14}$は平行四辺形である。
グラフは下のとおりで
$\hspace{6em}$
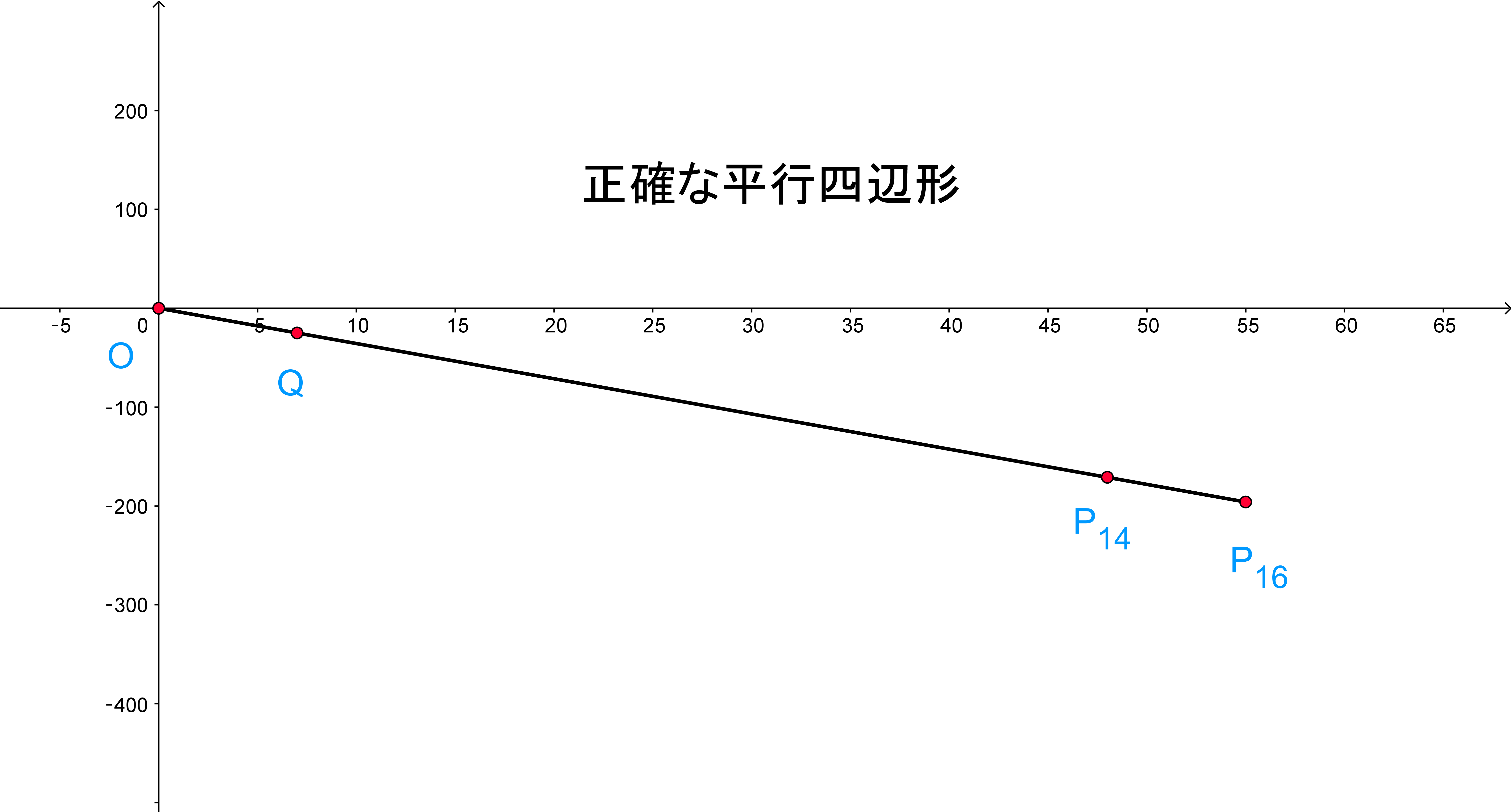
ほとんどつぶれた平行四辺形である。
下の図は見やすいように変形してあります。
$\hspace{6em}$
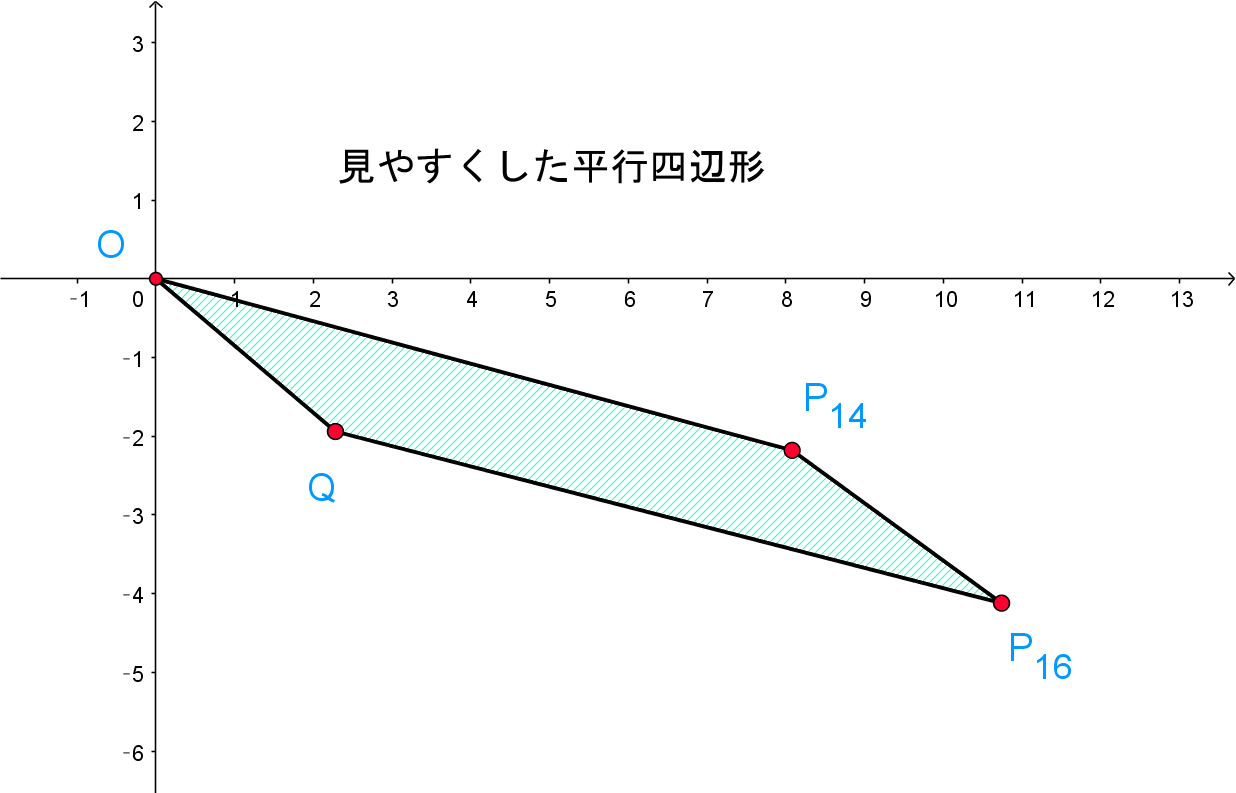
四角形$OQP_{16}P_{14}$の周および内部に含まれる格子点$(x,y)$をまともに求めるのは
かなり困難です。うまい手は、
$\hspace{3em}$ 一次変換(アフィン変換)
することです。しかし、今の受験生の使用している教科書には行列や一次変換は載っていませんので、自分で学習するしかありません。
(まさか出題者はそのことを知らなかったなんてことはないと思いますが …)
点$(x,y)を一次変換した点を(x',y')$とすると
\[ \left\{ \begin{array}{l} x'=ax+by\\ y'=cx+dy\\ \end{array} \right. \] $Q(7,-25)\ はy'軸上の点に写るとすると \qquad 0=7a-25b より a=25,\quad b=7$
$P_{14}(48,-171) は$x'$軸上の点に写るとすると \qquad 0=48c-171d より c=171,\quad d=48$
よって
\[ \left\{ \begin{array}{l} x'=25x+7y\\ y'=171x+48y\\ \end{array} \right. \]
$\hspace{2em} O(0,0) \rightarrow \ O'(0,0)$
$\hspace{2em} Q(7,-25) \rightarrow \ Q'(0,-3)$
$\hspace{2em} P_{14}(48,-171) \rightarrow \ P'_{14}(3,0)$
$\hspace{2em} P_{16}(55,-196) \rightarrow \ P'_{16}(3,-3)$
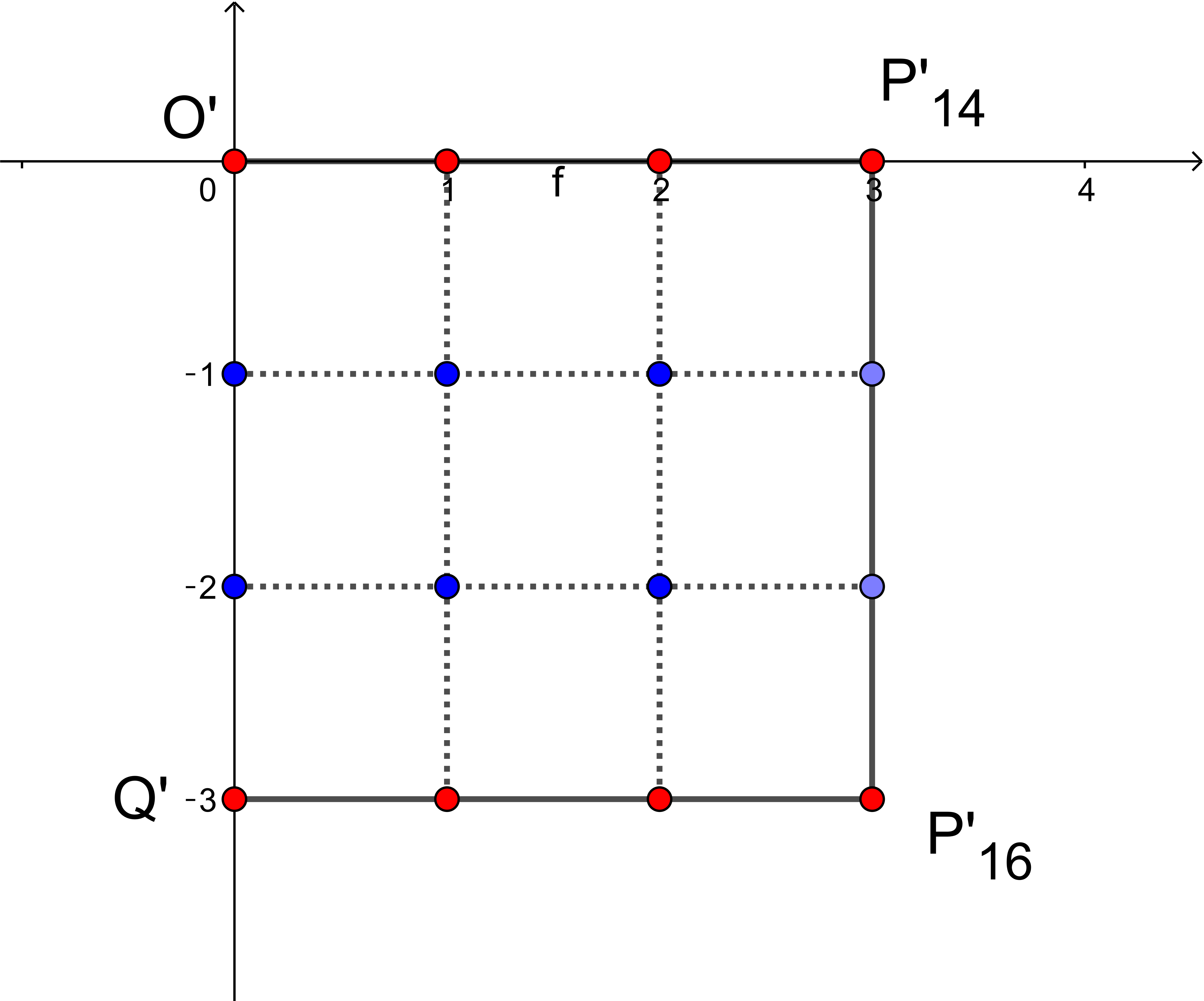
に写り、四角形$O'Q'P'_{16}P'_{14}$は正方形となる。
$(x,y)$が格子点ならば、$(x',y')$は格子点であるが、この逆については
上の一次変換を逆に解いて
\[ \left\{ \begin{array}{l} x=16x'-\cfrac{7}{3}y'\\ y=-57x'+\cfrac{25}{3}y'\\ \end{array} \right. \] したがって、格子点$(x',y')を戻した点(x,y)$がまた、格子点になるのは
$y'が3$の倍数のときであるから(図の赤点)
$\hspace{2em} (0,0) \rightarrow (0,0)$
$\hspace{2em} (1,0) \rightarrow (16,-57)$
$\hspace{2em} (2,0) \rightarrow (32,-114)$
$\hspace{2em} (3,0) \rightarrow (48,-171)$
$\hspace{2em} (0,-3) \rightarrow (7,-25)$
$\hspace{2em} (1,-3) \rightarrow (23,-82)$
$\hspace{2em} (2,-3) \rightarrow (39,-139)$
$\hspace{2em} (3,-3) \rightarrow (55,-196)$
の$8$点である。
一次変換の性質
座標平面上の平行な線分は、また平行な線分に写すので、平行四変形は平行四辺形に写ります。
メインメニュー に戻る